深度学习(7)——艺术风格的神经算法
艺术风格的神经算法
A Neural Algorithm of Artistic Style
Mr. Gatys有三篇关于风格迁移的文章,这是第二篇,其余两篇请看上一篇译文和下一篇译文
其中有详细的公式推导
译文,未校对
如有错误请见谅
摘要
在美术,尤其是绘画中,人类已经掌握了通过在图像的内容和风格之间构成复杂的相互作用来创造独特视觉体验的技能。到目前为止,该过程的算法基础是未知的,并且不存在具有类似能力的人工系统。然而,在视觉感知的其他关键领域,如物体和人脸识别,最近由一类被称为深度神经网络的生物启发视觉模型证明其近乎人类的表现.这里我们介绍一种基于深度神经网络的人工系统创造了这种高感性质量的艺术形象。该系统使用神经表示来分离和重新组合任意图像的内容和风格,提供用于创建艺术图像的神经算法。此外,鉴于性能优化的人工神经网络与生物视觉之间惊人的相似性,我们的工作为理解人类如何创造和感知艺术图像的算法提供了一条道路。
概述
在图像处理任务中最强大的深度神经网络类称为卷积神经网络。 卷积神经网络由小型计算单元层组成,使用前馈方式分层处理视觉信息(图1)。 每层单元可以被理解为图像滤波器的集合,每个图像滤波器从输入图像中提取特定特征。 因此,给定层的输出包括所谓的特征映射:输入图像的不同滤波版本。
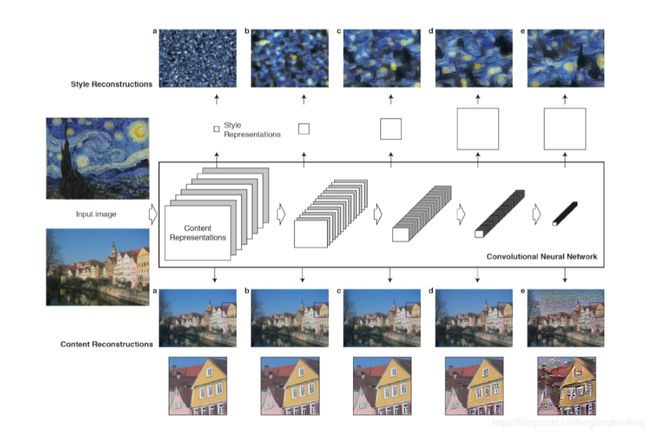
图1:卷积神经网络(CNN)。
给定输入图像在CNN中的每个处理阶段表示为一组滤波图像。虽然不同过滤器的数量沿着处理层级增加,但是过滤图像的大小通过一些下采样机制(例如,最大池化)而减小,导致每层网络的单元总数减少。内容重建。我们可以通过仅知道网络在特定层中的响应来重建输入图像,从而在CNN中的不同处理阶段可视化信息。我们从原始层’conv1_2’(a),‘conv2_2’(b),‘conv3_2’(c),‘conv4_2’(d)和’conv5_2’(e)重建输入图像VGG的网络。我们发现从较低层重建几乎是完美的(a-c)。在网络的较高层中,丢失详细的像素信息,同时保留图像的高级内容(d,e)。风格重建。在原始CNN激活之上,我们使用一个捕获输入图像纹理信息的特征空间。样式表示计算CNN的不同层中的不同特征之间的相关性。我们从构建在CNN层的不同子集上的样式表示重建输入图像的样式(‘conv1_1’(a),‘conv1_1’和’conv2_1’(b),‘conv1_1’,‘conv2_1’和’conv3_1’(c),‘conv1_1’,‘conv2_1’,‘conv3_1’和’conv4_1’(d),‘conv1_1’,‘conv2_1’,‘conv3_1’,'conv4_1 ‘和’conv5_1’(e)。这将创建与增加规模的给定图像的样式匹配的图像,同时丢弃场景的全局排列的信息。
当卷积神经网络在物体识别方面受到训练时,它们开发了一种图像表示,使得对象特征信息沿着处理层次越来越明显。因此,随着网络的处理层次的深入,相对于详细的像素值,输入图像被转换为越来越受关注的实际内容表示。我们可以通过仅从该层中的特征图重建图像来直接可视化每层包含的关于输入图像的信息(图1,内容重建,参见方法以获得关于如何重建图像的细节)。网络中的较高层根据对象及其在输入图像中的排列捕获高级内容,但不限制重建的确切像素值(图1,内容重建d,e)。相反,来自较低层的重建简单地再现原始图像的精确像素值(图1,内容重建a,b,c)。因此,我们将网络的较高层中的特征响应称为内容表示。
为了获得输入图像样式的表示,我们使用最初设计用于捕获纹理信息的特征空间。此特征空间构建在网络的每个层中的过滤器响应之上。 它由特征图空间范围内不同滤镜响应之间的相关性组成(详见方法)。 通过包括多个层的特征相关性,我们获得输入图像的静态多尺度表示,其捕获其纹理信息而不是全局布置。
同样,我们可以通过构建与给定输入图像的样式表示相匹配的图像来可视化由构建在网络的不同层上的这些样式特征空间捕获的信息(图1,样式重建).10,11确实从样式重建功能产生输入图像的纹理化版本,捕获其在颜色和局部结构方面的一般外观。此外,来自输入图像的局部图像结构的大小和复杂性沿着层次结构增加,这可以通过增加的感受野大小和特征复杂性来解释。我们将这种多尺度表示称为样式表示。
图2.将照片内容与几种着名艺术品的风格相结合的图像。
通过找到同时匹配照片的内容表示和艺术品的样式表示的图像来创建图像。A(照片:Andreas Praefcke)为描绘德国图宾根的Neckarfront的原始照片。 为每个生成的图像提供样式的绘画显示在每个面板的左下角。 图B为J.M.W.Turner的牛头怪残骸(1805),图C为文森特梵高的星光之夜(1889),图D为Der Schrei的Edvard Munch(1893),图E为Pablo Picasso的Femme nue assise(1910),图F为Wassily Kandinsky的Composition VII(1913)。
本文的主要发现是卷积神经网络中内容和风格的表达是可分的。也就是说,我们可以独立地操纵两个表示以产生新的感知上有意义的图像。为了证明这一发现,我们生成了混合来自两个不同源图像的内容和样式表示的图像。特别地,我们匹配描绘德国图宾根的“Neckarfront”图像的内容表示以及从不同艺术时期拍摄的几个着名艺术品的样式表示(图2)。
图3.匹配内容的相对权重和各个源图像的样式。
匹配内容和匹配样式之间的比率α/β从左上到右下增加。 高度强调风格有效地产生了样式图像的纹理化版本(左上)。 高度重视内容会产生只有少量风格化的图像(右下角)。 在实践中,可以在两个极端之间平滑地插值。
如上所述,样式表示是包括神经网络的多个层的多尺度表示。 在我们在图2中示出的图像中,样式表示包括来自整个网络层次结构的层。 通过仅包括较少数量的较低层,也可以更局部地定义样式,从而导致不同的视觉体验(图3,沿着行)。 当将样式表示匹配到网络中的更高层时,局部图像结构在越来越大的范围内匹配,从而导致更平滑和更连续的视觉体验。 因此,通常通过将样式表示匹配到网络中的最高层(图3,最后一行)来创建视觉上最吸引人的图像。
当然,图像内容和风格不能完全解开。当将一个图像的内容和另一个图像的样式合成一个新的图像时,通常不存在同时完全匹配两个约束的图像。然而,我们在图像合成期间最小化的损失函数分别包含内容和样式,它们是完全分离的(参见方法)。因此,我们可以顺利地调整重构内容或样式的重点(图3,沿着列)。对样式的强调将导致图像与艺术品的外观相匹配,有效地给出了纹理版本,但几乎没有显示任何照片的内容(图3,第一列)。当强调内容时,可以清楚地识别照片,但绘画的样式不是很匹配(图3,最后一栏)。对于特定的一对源图像,可以调整内容和样式之间的权衡以创建视觉上吸引人的图像。
在这里,我们提出了一种人工神经系统,它实现了图像内容与样式的分离,从而允许以任何其他图像的样式重铸一个图像的内容。我们通过创造新的艺术图像来展示这一点,这些图像将几种着名绘画的风格与任意选择的照片的内容相结合。特别地,我们从在物体识别上训练的高性能深度神经网络的特征响应导出图像的内容和样式的神经表示。据我们所知,这是第一次在整个自然图像中分离内容与风格的图像特征。
以前关于将内容与风格分离的工作是在复杂度较低的感官输入上进行评估,例如不同手写字符或面部图像或不同的姿势小图形。
在我们的演示中,我们以一系列着名艺术品的风格呈现一张特定的照片。这个问题通常在称为非照片写实渲染的计算机视觉分支中进行(最近的评论见14)。从概念上讲,最密切相关的是使用纹理转移来实现艺术风格转移。然而,这些先前的方法主要依靠非参数技术来直接操纵图像的像素表示。相比之下,通过使用在物体识别上训练的深度神经网络,我们在明确表示图像的高级内容的特征空间中进行操纵。
受过物体识别训练的深度神经网络的特征以前用于风格识别,以便根据创作时间对艺术品进行分类。在那里,分类器在原始网络激活之上进行训练,我们称之为内容表示。我们推测,转换为静态特征空间(例如我们的样式表示)可能会在样式分类中实现更好的性能。
一般来说,我们混合不同来源的内容和风格的图像方法,提供了一种新的、有吸引力的工具来研究艺术,风格和内容独立的图像外观的感知和神经表示。我们可以设计新颖的刺激,引入两个独立的,感知上有意义的变异来源:图像的外观和内容。我们设想这对于从心理物理学到功能成像甚至电生理学神经记录的视觉感知的广泛实验研究是有用的。实际上,我们的工作提供了一种算法理解,即神经表示如何独立地捕获图像的内容及其呈现的样式。重要的是,我们的风格表征的数学形式产生了一个清晰的、可测试的假设,即关于图像外观到单个神经元水平的表示。样式表示简单地计算网络中不同类型神经元之间的相关性。提取神经元之间的相关性是一种生物学上合理的计算,例如,通过主要视觉系统中的所谓复杂细胞(V1)实现.21我们的结果表明,在腹侧的不同处理阶段执行复杂细胞计算流将是获得视觉输入外观的与内容无关的表示的可能方式。
总而言之,神经系统经过训练以执行生物视觉的核心计算任务之一,自动学习允许图像内容与风格分离的图像表示,这真是令人着迷。解释可能是在学习对象识别时,网络必须对保留对象身份的所有图像变化保持不变。将图像内容的变化及其外观变化分解的表示对于该任务是非常实用的。因此,我们从风格中抽象内容的能力以及我们创作和欣赏艺术的能力可能主要是我们视觉系统强大的推理能力的卓越标志。
方法
主要文本中提出的结果是在VGG网络的基础上生成的,这是一个卷积神经网络,可以在一个共同的视觉对象识别基准任务上与人类表现相媲美23,并在2002年进行了广泛的描述。我们使用了提供的特征空间。 由19层VGGNetwork的16个卷积层和5个池层组成。 我们不使用任何完全连接的层。该模型是公开的,可以在caffe框架中进行探索.24对于图像合成,我们发现用平均池替换最大池操作可以改善梯度流,并且可以略微获得 更吸引人的结果,这就是为什么所显示的图像是用平均汇集生成的。
通常,网络中的每个层定义非线性滤波器组,其复杂性随着网络中层的位置而增加。 因此,通过对该图像的滤波器响应,在CNN的每个层中编码给定的输入图像 x ⃗ \vec{x} x。 具有 N l N_l Nl个不同滤波器的层具有尺寸为 M l M_l Ml的 N l N_l Nl个特征图,其中 M l M_l Ml是高度乘以特征图的宽度。 因此, l l l层中的响应可以存储在矩阵 F l ∈ R N l × N l F^l\in R^{N^l×N^l} Fl∈RNl×Nl中,其中是 l l l层中位置 j j j处的第 i i i个滤波器的激活。 为了可视化在层次结构的不同层处编码的图像信息(图1,内容重建),我们对白噪声图像执行梯度下降以找到与原始图像的特征响应匹配的另一图像。 因此,令 p ⃗ \vec{p} p和 x ⃗ \vec{x} x是原始图像和生成的图像,并且 P l P_l Pl和 F l F_l Fl是它们在 l l l层中的相应特征表示。 然后我们定义两个特征表示之间的平方误差损失
KaTeX parse error: Expected '}', got '\cal' at position 3: {\̲c̲a̲l̲ ̲L}_{content}(\v…
相对于层 l l l中的激活,该损失的导数等于
KaTeX parse error: Expected '}', got '\cal' at position 18: …frac{\partial {\̲c̲a̲l̲ ̲L}_{content}}{\…
从中可以使用标准误差反向传播来计算关于图像 x ⃗ \vec{x} x的梯度。 因此,我们可以改变初始随机图像 x ⃗ \vec{x} x,直到它在CNN的某一层中产生与原始图像 p ⃗ \vec{p} p相同的响应。 图1中的五个内容重建来自最初的VGG网络的’conv1_1’(a),‘conv2_1’(b),‘conv3_1’©,‘conv4_1’(d)和’conv5_1’(e)层 。
在网络的每一层中的CNN响应之上,我们构建了一种样式表示,其计算不同滤波器响应之间的相关性,其中期望是在输入图像的空间扩展上获得的。 这些特征相关性由Gram矩阵 G l ∈ R N l × N l G^l\in R^{N^l×N^l} Gl∈RNl×Nl给出,其中 G i j l G^l_{ij} Gijl是层 l l l中的矢量化特征映射 i i i和 j j j之间的内积:
(3) G i j l = ∑ k F i k l F j k l G^l_{ij} = \sum_k F^l_{ik}F^l_{jk} \tag{3} Gijl=k∑FiklFjkl(3)
为了生成与给定图像的样式匹配的纹理(图1,样式重建),我们使用来自白噪声图像的梯度下降来找到与原始图像的样式表示匹配的另一图像。 这是通过最小化来自原始图像的Gram矩阵的条目与要生成的图像的Gram矩阵之间的均方距离来完成的。 令 a ⃗ \vec{a} a和 x ⃗ \vec{x} x是原始图像和生成的图像,并且 A l A^l Al和 G l G^l Gl是它们在 l l l层中的相应样式表示。 然后,第 l l l层对总损失的贡献
(4) E l = 1 4 N l 2 M l 2 ∑ i , j ( G i j l − A i j l ) 2 E_l = \frac{1}{4N^2_lM^2_l}\sum_{i,j} (G^l_{ij} - A^l_{ij})^2 \tag{4} El=4Nl2Ml21i,j∑(Gijl−Aijl)2(4)
总的样式损失是
KaTeX parse error: Expected '}', got '\cal' at position 3: {\̲c̲a̲l̲ ̲L}_{style}(\vec…
其中 w l w_l wl是每层对总损失的贡献的加权因子(参见下面我们的结果中 w l w_l wl的具体值)。 关于 l l l层中的激活的 E l E_l El的导数可以通过分析计算:
(6) ∂ E l ∂ F i j l = { 1 N l 2 M l 2 ( ( F l ) T ( G l − A l ) ) j i , if F i j l > 0 0 , if F i j l < 0 \frac{\partial E_l}{\partial F^l_{ij}} = \begin{cases} \frac{1}{N^2_lM^2_l}((F^l)^T(G^l-A^l))_{ji}, & \text {if $F^l_{ij}>0$} \\ 0, & \text{if $F^l_{ij}<0$} \end{cases} \tag{6} ∂Fijl∂El={Nl2Ml21((Fl)T(Gl−Al))ji,0,if Fijl>0if Fijl<0(6)
可以使用标准误差反向传播容易地计算 E l E_l El相对于网络的较低层中的激活的梯度。 图1中的五种样式重建是通过匹配网络层 ‘conv1_1’(a),‘conv1_1’和’conv2_1’(b),‘conv1_1’,'conv2_1’和’conv3_1’©,‘conv1_1’,‘conv2_1’,‘conv3_1’和’conv4_1’(d),‘conv1_1’,‘conv2_1’,‘conv3_1’,‘conv4_1’和’conv5_1’(e)上的样式表示来生成的。
为了生成将照片内容与绘画风格混合的图像(图2),我们共同最小化白噪声图像与网络的一层中的照片的内容表示的距离以及该图像的样式表示。 在CNN的多个层中绘画。 所以我们让 p ⃗ \vec{p} p成为照片, a ⃗ \vec{a} a是艺术品。 我们最小化的损失函数是
KaTeX parse error: Expected '}', got '\cal' at position 3: {\̲c̲a̲l̲ ̲L}_{total}(\vec…
其中 α \alpha α和 β \beta β分别是内容和样式重建的加权因子。 对于图2中所示的图像,我们匹配层’conv4_2’上的内容表示和 层’conv1_1’,‘conv2_1’,‘conv3_1’,‘conv4_1’和’conv5_1’上的样式表示( 在这些层中 w l w_l wl= 1/5,其他层 w l w_l wl = 0)。 比率 α / β \alpha/\beta α/β为 1 × 1 0 − 3 1×10^{-3} 1×10−3(图2B,C,D)或 1 × 1 0 − 4 1×10^{-4} 1×10−4(图2E,F)。 图3显示了内容和样式重建损失(沿着列)的不同相对权重的结果,以及仅在层’conv1_1’(a),‘conv1_1’和’conv2_1’(b),‘conv1_1’,'conv2_1’和’conv3_1’©,‘conv1_1’,‘conv2_1’,‘conv3_1’和’conv4_1’(d),‘conv1_1’,‘conv2_1’,‘conv3_1’,‘conv4_1’和’conv5_1’(e)上匹配样式表示的结果。因子 w l w_l wl总是等于1除以具有非零损失权重 w l w_l wl的活动层的数量。