深度学习（11）——DeepLab v1

DeepLab v1

DeepLab 由谷歌团队提出的，至今有了四个版本，也就是v1-v4。其结合了深度卷积神经网络（DCNNs）和概率图模型。

在论文《Semantic image segmentation with deep convolutional nets and fully connected CRFs》中提出，发表在 ICLR 2015 。

论文的写作时间是2014年，当时深度卷积神经网络在高级视觉研究领域取得了突破。其卷积和池化操作保证了其不变性，能够提取高级抽象特征。不变性指的是平移不变性，卷积层扩大感知野，池化层的pooling操作，即使图像有小的位移、缩放、扭曲等，提取到的特征依然会保持不变，减小了相对空间位置的影响。这在高级特征提取中作用重大，但在一些低级视觉研究，如语义分割任务中效果是不理想的。我们希望获取具体的空间信息，而这些信息随着网络的加深慢慢丢失掉。

于是对于语义分割任务，DCNN存在两个问题。

第一，最大池化和下采样操作压缩了图像分辨率。一般语义分割通过将网络的全连接层改为卷积层，获取得分图（或称为概率图、热图），然后对其上采样、反卷积等操作还原与输入图像同样大小。如果压缩太厉害，还原后分辨率就会比较低，因此我们希望获得更为稠密（dense）或尺寸更大的得分图；第二，对空间变换的不变性限制了模型的精度，网络丢失了很多细节，获得的概率图会比较模糊，我们希望获得更多的细节。在该文章中，提出使用空洞算法和全连接CRF分别解决这两个问题。

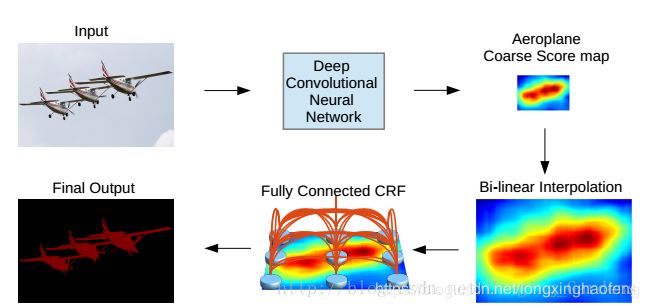
DeeplabV1方法分为两步走，第一步仍然采用了DCNNs得到 coarse score map并插值到原图像大小，然后第二步借用fully connected CRF对从FCN得到的分割结果进行细节上的refine。

该方法的创新之处在于将DCNNs的特征图与全连接CRF结合，并将Hole（空洞卷积）应用在DCNNs中。

DCNNs基于VGG16模型，网络结构图如下：

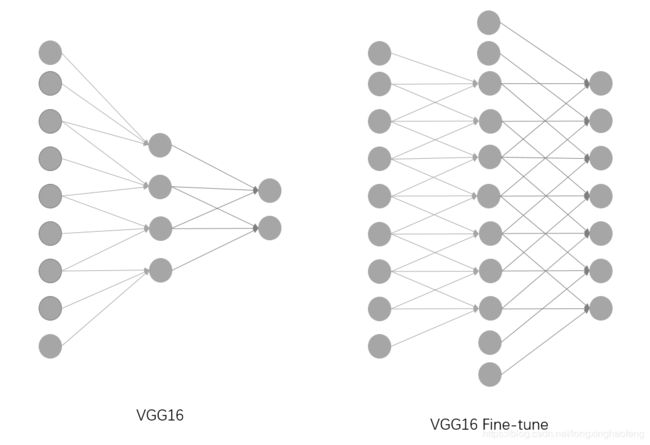
在VGG16中，卷积层的卷积核大小统一为 33 ，步长为 1，最大池化层的池化窗口为 2 * 2 ，步长为2 。

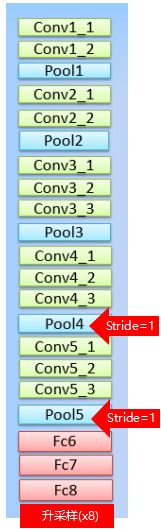
在这基础上做的改进是使用 11 的卷积层代替FC层，那么就变成了全卷积网络，输出得到的是得分图，也可以理解成概率图。将pool4和pool5的步长由2改为1， 这样在原本FC7的位置，VGG网络总的步长由原来的32变为8（总步长=输入size/特征图size）。一般来说，池化层的步长为2，池化后输出大小变为输入大小的一半。原VGG16模型有5次池化，缩小 $2^5=32$ 倍，修改后的VGG16有3次补步长为2的池化，缩小 $2^3=8$ 倍，两次步长为1的池化，输出大小基本不变，所以说VGG网络总的步长由原来的32变为8。

这样改的原因是为了获得更为稠密（dense）的score map。

一旦修改了网络结构，就会面临一个问题，如何既想使用预训练好的网络模型进行微调，又能改变网络结构获得更为稠密的得分图。

感知也（RF）改变，这对使用预训练的网络有何影响？

感知野计算

感知野就是当前这一层的节点往前能看到多少前些层的节点，

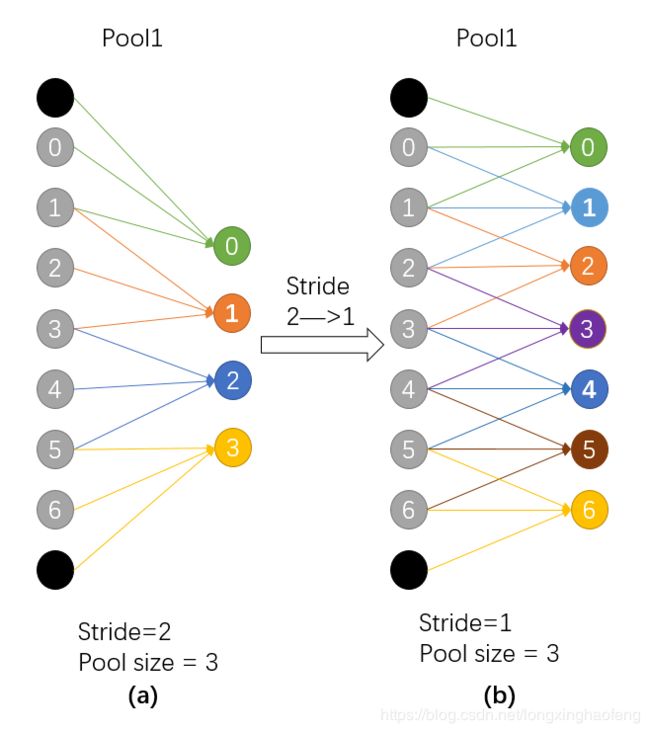
由上图所示，左侧(a)(b)图表示一维卷积层的步长由2变为1后，感知野的变化。(a)输出4个节点，0-3，每个节点的感知野为3；(b)输出7个节点，0-6 ，每个节点的感知野为3。图a的输出0123对于图b输出的0246，感知野相同，但又多了其他节点，使得得分图变得更加稠密。

这里解释一下padding为什么不算在感知野里面，一种直观的方式是，一层的padding一般只有两三个节点，而深度神经网络中每一层的输出有几百上千的节点，而padding只能影响到4-6个节点，这对于一层的输出节点来说是微不足道的。

©的下一层采用hole算法,(d)的第三个2输出来自©的0,2,4，这对应(a)中输出的123，所以d层有b层的所有内容，同时又增加到7个输出(相比与b层的2个输出)，所以输出变得稠密了。

很明显，为了保证感知野不变，我们对卷积层滤波器进行了扩张，这就是空洞算法。

使用hole算法后，滤波器 $k$ 大小变化为
$$k=k+(k-1)(hloesize-1)$$
如图，假设原始滤波器大小为3，hole 大小为2，那么扩张后滤波器大小为 5 。扩张部分用0填充。

感知野计算由输入层后的第一层开始依次往后计算

第一层卷积层的输出特征图像素的感受野的大小等于滤波器的大小

感受野计算公式
$$\begin{gathered} S_n=S_{n-1}\ast s \\ R{F}_n=R{F}_{n-1}+(k_n-1)\ast S_{n-1} \end{gathered}$$
其中，$S_n$ 是网络前 $n$ 层strides，$s$ 是这一层的strides。$R{F}_n$ 是上一层的RF，$R{F}_{n-1}$ 是这一层的RF， $k_n$ 表示卷积核大小，padding对感受野无影响。

使用hole算法后，卷积核大小变化
$$k=k+(k-1)(hloesize-1)$$
以VGG16为例，计算感知野。
$$\begin{gathered} Conv1.1R_1=3,S_1=1 \\ Conv1.2R_2=R_1+(3-1)\ast S_1=5,S_2=S_1\ast 1=1 \\ Pool1R_3=R_2+(2-1)\ast S_2=6,S_3=S_2\ast 2=2 \\ Conv2.1R_4=R_3+(3-1)\ast S_3=10,S_4=S_3\ast 1=2 \\ Conv2.2R_5=R_4+(3-1)\ast S_4=14,S_5=S_4\ast 1=2 \\ Pool2R_6=R_5+(2-1)\ast S_5=16,S_6=S_5\ast 2=4 \\ Conv3.1R_7=R_6+(3-1)\ast S_6=24,S_7=S_6\ast 1=4 \\ Conv3.2R_8=R_7+(3-1)\ast S_7=32,S_8=S_7\ast 1=4 \\ Conv3.3R_9=R_8+(3-1)\ast S_8=40,S_9=S_8\ast 1=4 \\ Pool3R_{10}=R_9+(2-1)\ast S_9=44,S_{10}=S_9\ast 2=8 \\ Conv4.1R_{11}=R_{10}+(3-1)\ast S_{10}=60,S_{11}=S_{10}\ast 1=8 \\ Conv4.2R_{12}=R_{11}+(3-1)\ast S_{11}=76,S_{12}=S_{11}\ast 1=8 \\ Conv4.3R_{13}=R_{12}+(3-1)\ast S_{12}=92,S_{13}=S_{12}\ast 1=8 \\ Pool4R_{14}=R_{13}+(2-1)\ast S_{13}=100,S_{14}=S_{13}\ast 2=16 \\ Conv5.1R_{15}=R_{14}+(3-1)\ast S_{14}=132,S_{15}=S_{14}\ast 1=16 \\ Conv5.2R_{16}=R_{15}+(3-1)\ast S_{15}=164,S_{16}=S_{15}\ast 1=16 \\ Conv5.3R_{17}=R_{16}+(3-1)\ast S_{16}=196,S_{17}=S_{16}\ast 1=16 \\ Pool5R_{18}=R_{17}+(2-1)\ast S_{17}=212,S_{18}=S_{17}\ast 2=32 \\ fc6R_{19}=R_{18}+(1-1)\ast S_{18}=212,S_{19}=S_{18}\ast 1=32 \\ fc7R_{20}=R_{19}+(1-1)\ast S_{19}=212,S_{20}=S_{19}\ast 1=32 \end{gathered}$$
pool4的stride由2变为1，则紧接着的conv5_1, conv5_2和conv5_3中hole size为2。接着pool5由2变为1, 则后面的fc6中hole size为4。 计算感知野。
$$\begin{gathered} Pool4R_{14}=R_{13}+(2-1)\ast S_{13}=100,S_{14}=S_{13}\ast 1=8 \\ Conv5.1R_{15}=R_{14}+(5-1)\ast S_{14}=132,S_{15}=S_{14}\ast 1=8 \\ Conv5.2R_{16}=R_{15}+(5-1)\ast S_{15}=164,S_{16}=S_{15}\ast 1=8 \\ Conv5.3R_{17}=R_{16}+(5-1)\ast S_{16}=196,S_{17}=S_{16}\ast 1=8 \\ Pool5R_{18}=R_{17}+(2-1)\ast S_{17}=212,S_{18}=S_{17}\ast 1=8 \\ fc6R_{19}=R_{18}+(1-1)\ast S_{18}=212,S_{19}=S_{18}\ast 1=8 \\ fc7R_{20}=R_{19}+(1-1)\ast S_{19}=212,S_{20}=S_{19}\ast 1=8 \end{gathered}$$

为什么要保证感知野大小不变

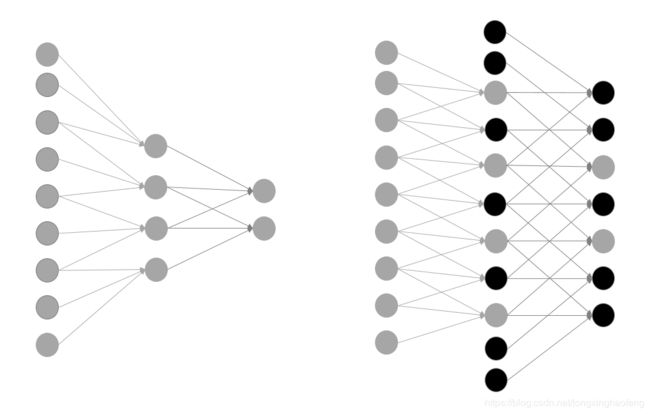
使用预训练模型，一是使用其网络结构，二是使用训练好的权重来进行初始化。

如图所示，这里我们对网络结构进行了微调，增加了一些网络节点，并且保证感知野大小不变。

如右侧图像所示，只需要在新增加的节点处初始化为0（黑色节点），就可以使用预训练好的权重进行初始化。

Fully connected CRF

CNN是一个逐步提取特征的部分，原始位置信息会随着网络深度的增加而减少或消失。CRF在传统图像处理上的应用是做一个平滑。CRF简单说，是在决定一个位置的像素值时（paper里是label），会考虑周围像素点的值（label）。但是通过CNN得到的概率图在一定程度上已经足够平滑，所以短程的CRF没有太大的意义。于是考虑使用Fully connected CRF，这样就会综合考虑全局信息，恢复详细的局部结构，如精确图形的轮廓。CRF几乎可以用于所有的分割任务中图像精度的提高。

CRF是后处理，是不参与训练的，在测试时对特征提取后得到的得分图进行双线性插值，恢复到原图尺寸，然后再进行CRF处理，因为缩小8倍的，所以直接放大到原图是可以接受的。如果是32倍，则需要上采样（反卷积）。

第一列是原图像和Ground Truth；第二列是DCNN的输出，上面是得分图（Score map），下面是置信图（Belief map）。最后一个DCNN层的输出用作CRF的输入。后面三列分别是CRF迭代1、2、10次后的得分图和置信图。

CRF中使用的是softmax后的概率图。

令随机变量 $x_i$ 是像素 $i$ 的标签， $x_i\in L=\left\{l_1,l_2,\cdots ,l_L\right\}$ ，$L$ 是语义标签。令隐藏标签变量 $X=\left\{x_1,x_2,\cdots ,x_N\right\}$，$N$就是图像的像素个数，全局观测是 $I=\left\{i_1,i_2,\cdots ,i_N\right\}$ ，要根据全局观测像素 $I$ 推测标签变量 $X$ 。 可以建立CRF模型，其条件概率为：
$$P(X|I)=\frac{1}{Z}\exp (-E(x|I))$$
规范化因子为 $Z$ ，对所有分子求和得到，以确保 $P(X)$ 是被正确定义的概率。
$$Z=\sum exp(-E(x|I))$$
势函数 $\psi =exp(-E(x|I))$ ：用于定义在全局观测 $I$ 下，$x$ 之间的相关关系。

能量函数：
$$E(x)=\sum _i{\theta }_i(x_i)+\sum _{ij}{\theta }_{ij}(x_i,x_j)$$
能量越大，势能越小，概率越小。

上式中，第一项仅考虑单节点，也就是一元能量项 ${\theta }_i(x_i)$ ,他代表将像素 $i$ 判别（条件随机场是判别模型）成label $x_i$ 的能量。一元能量项直接来自于前端的FCN，FCN输出的是概率 $P(x_i)$，所以 ${\theta }_i(x_i)=-\log P(x_i)$ 。

第二项考虑一对节点的关系，也就是二元能量项 ${\theta }_{ij}(x_i,x_j)$ ，他鼓励相似（距离小）像素分配相同的标签，相差较大的像素分配不同的标签，而这个“距离”的定义与颜色值和实际相对距离有关。
$${\theta }_{ij}(x_i,x_j)=\mu (x_i,x_j)\left[w_{1}exp(-\frac{||p_i-p_j|{|}^2}{2{\sigma }_{\alpha }^2}-\frac{||I_i-I_j|{|}^2}{2{\sigma }_{\beta }^2})+w_{2}exp(-\frac{||p_i-p_j|{|}^2}{2{\sigma }_{\gamma }^2})\right]$$
当 $x_i̸=x_j$ 时， $\mu (x_i,x_j)=1$ ，否则为零。也就是说，只有当标签不同时，才会有第二项，才会增大能量 $E$。

中括号中的表达式是在不同特征空间的两个高斯核函数，第一个基于双边高斯函数基于像素位置 $p$ 和像素颜色强度 $I$，强制相似RGB和位置的像素分在相似的label中，第二个只考虑像素位置，等于施加一个平滑项。 超参数 ${\sigma }_{\alpha },{\sigma }_{\beta },{\sigma }_{\gamma }$ 控制高斯核的权重。

对于一张图像来说，我们把它看成图模型 $G=(V,E)$，图模型的每个顶点对应一个像素点，即 $V=\left\{i_1，i_2，\cdots ,i_n\right\}$。对于边来说，

(1)如果是稀疏条件随机场，那么我们构造图模型的边集合 $E$ 就是：每对相邻的像素点间可以构造一条边。当然除了4邻域构造边之外，你也可以用8邻域模型。

(2)全连接条件随机场与稀疏条件随机场的最大差别在于：每个像素点都与所有的像素点相连接构成连接边。而二元势函数描述的是每一个像素与其他所有像素的关系，所以叫“全连接”。

参考

谷歌——DeepLab v1

【语义分割】- DeeplabV1&V2

感知野理解及其计算方法

卷积神经网络物体检测之感受野大小计算

对卷积层dilation膨胀的作用的理解，caffe-ssd dilation Hole算法解析

从FCN到DeepLab