深度学习(12)——用于对象分割和细粒度本地化的超列
用于对象分割和细粒度本地化的超列
- 1、上采样
- 2、超列
- 3、网格分类器
- 4、分块分类
- 5、神经网络
Hypercolumns for Object Segmentation and Fine-grained Localization
1、上采样
图像放大几乎都是采用内插值方法,即在原有图像像素的基础上,在像素点之间采用合适的插值算法插入新的元素。双线性插值是目前在语义分割中用的比较多的一种方式,比如FCN中就是用的这种方法。 这种方法特点是不需要进行学习,运行速度快,操作简单。只需要设置好固定的参数值即可,设置的参数就是中心值需要乘以的系数。
疑问:直接resize得到结果不可以吗,同样都是双线性插值
线性插值使用连接两个已知量的直线来确定在这个两个已知量之间的一个未知量的值的方法,如图1
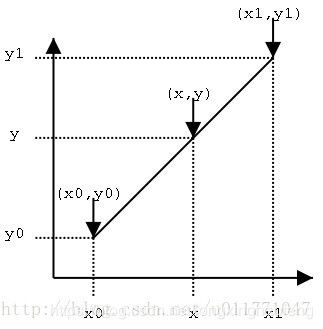
双线性插值是线性插值的扩展。利用原图像中目标点四周的四个真实存在的像素值来共同决定目标图中的一个像素值,其核心思想是在两个方向分别进行一次线性插值。如图2所示,由 Q 12 Q_{12} Q12和 Q 22 Q_{22} Q22确定点 R 2 R_2 R2, 由 Q 11 Q_{11} Q11和 Q 21 Q_{21} Q21确定点 R 1 R_1 R1,最终由点 R 2 R_2 R2和 R 1 R_1 R1确定点 p p p 。
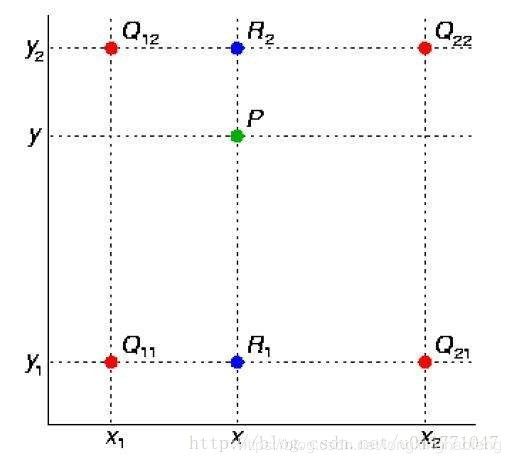
而在实际应用中呢,首先设置参数 α \alpha α,已知 k e r n e l s i z e = 64 kernel size=64 kernelsize=64,根据某种规则生成 64 × 64 64 \times 64 64×64大小的矩阵。若原始图片大小是 16 × 16 16 \times 16 16×16,那么就需要 16 × 16 16 \times 16 16×16个 64 × 64 64 \times 64 64×64的 α \alpha α 矩阵,原始图像的每一个像素放置在 α \alpha α 矩阵中央,这样每两个像素之间都可以进行双线性插值,相邻元素之间插入 32 32 32个像素,周边补充 32 32 32个像素。不同元素对插入值有着不同的影响,则互相叠加,最后将原始图像的 16 × 16 16 \times 16 16×16个像素移除,也就形成了 32 × 17 32\times17 32×17(周边补充 16 + 1 16+1 16+1) = 544 =544 =544 ,最终上采样大小为 ( 544 , 544 ) (544, 544) (544,544)。
2、超列
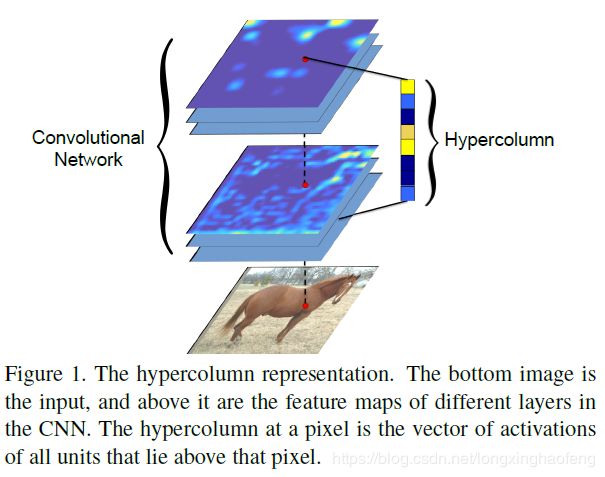
在卷积网络的各个层中,我们称接近输入层的卷积层为底层卷积层,接近输出层的卷积层为高层卷积层。那么底层卷积层得到的feature map中包含的低级信息,如姿势,照明,清晰度,空间位置等信息越多,高层卷积层得到的feature map得到的特征越抽象、语意信息越多。卷积网络(CNN)的识别算法通常使用最后一层的输出作为特征表示。然而,该层中的信息在空间上可能太粗糙导致不能精确定位。为了更好的利用这两种信息,对于原始图像 i i i 位置的像素,我们同时利用部分或全部与 i i i 位置对应的的feature map。那么对于 i i i 位置的像素,我们就会得到一个特征向量,这个特征向量称为 i i i 的超列。
对于分割任务,我们resize边界框至 50 ∗ 50 50*50 50∗50 ,并预测一个相应的heatmap,heatmap编码的是对应位置在物体内部的概率。那么问题转化为对 50 ∗ 50 50*50 50∗50 个位置进行分类,文章使用超列进行分类。
由于卷积、池化的存在,feature map大小与原始图像大小并不相同,将各层feature map中的像素与原始图像 i i i 位置处的像素对应起来,就需要使用上采样(双线性插值),统一feature map大小至与原始图像大小相同。文章中对于检测分割任务,将边界框统一调整到 50 × 50 50\times 50 50×50 ,所以,原始图像的参考大小是 50 × 50 50\times 50 50×50 。如图3 所示:
文章中公式1为,
f i = ∑ k α i k F k f_i = \sum_k \alpha_{ik}F_k fi=k∑αikFk
可以写成
f k = α k F k f_{k} = \alpha_k F_k fk=αkFk
f = ∑ k f k f = \sum_k f_k f=k∑fk
F k F_k Fk 表示第 k k k个feature map , f k f_k fk表示第 k k k个feature map上采样后的feature map。超列 i i i位置的特征向量为 f i f_i fi。 α i k \alpha_{ik} αik取决于box和feature map中i和k的位置。
这里的累加符号表示将不同feature map的通道叠加在一起,而非将数值相加,最后输出还是 50 × 50 × c 50\times50\times c 50×50×c,即将网络中部分或全部feature map连接到一个长向量,我们称之为超列。例如,使用来自pool2(256个通道),conv4(384个通道)和fc7(4096个通道)将导致4736维向量。
为方便解释,上式中将公式1的 f i f_i fi替换成 f f f,但实际中超列只是针对某一位置而言,并非整个feature map,对于 i i i 位置的像素, f i f_i fi 才是 i i i 位置的超列。
3、网格分类器
由上一章节我们已知 f i f_i fi 是 i i i 位置的超列。
针对 50 × 50 50\times 50 50×50 的特征,最简单的办法是训练 50 × 50 50\times 50 50×50个分类器。但是考虑到训练速度及相邻像素点之间的相关关系,文章训练了 K × K K\times K K×K 个分类器, K = 5 o r 10 K = 5\,or\, 10 K=5or10 。每一个分类器实际上是一个函数 g k ( ⋅ ) g_k(\cdot) gk(⋅),它接受一个特征向量并输出 0-1之间的概率。
h i ( . ) = ∑ k α i k g k ( . ) h_i(.) = \sum_k \alpha_{ik}g_k(.) hi(.)=k∑αikgk(.)
如果第 i i i个像素的特征向量是 f i f_i fi ,则得分是
p i = ∑ k α i k g k ( f i ) = ∑ k α i k p i k p_i = \sum_k \alpha_{ik}g_k(f_i) = \sum_k \alpha_{ik}p_{ik} pi=k∑αikgk(fi)=k∑αikpik
其中 p i k p_{ik} pik 是第k个分类器为第i个像素输出的概率。因此,在测试时,我们在所有像素上运行所有 K 2 K^2 K2分类器。然后,在每个像素处,我们使用上面的等式线性组合该像素处的所有分类器的输出以产生最终预测。 注意,线性组合的系数( α \alpha α)取决于位置。
下图所示,是整个计算流程:
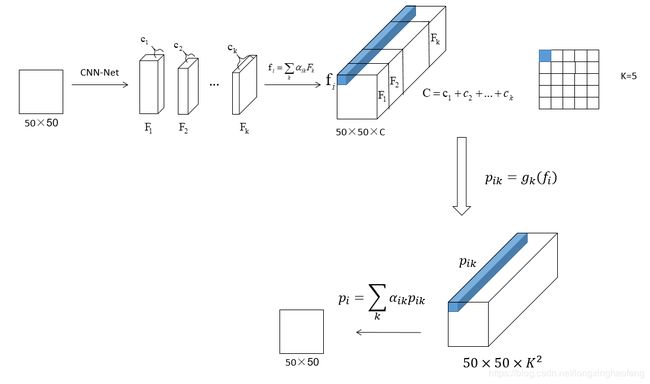
4、分块分类
上述过程是将所有的feature map大小调整到 50 × 50 50\times 50 50×50 ,然后对每个位置进行分类。但是以此计算成百上千的feature map的计算量太大,因此我们可以在相关位置将超列拆分,再进行计算。
每个具有c通道的feature map 将在超列中产生c维特征块位置的表示,并且该块将在分类器中具有相应的权重块。因此在线性组合 p i k p_{ik} pik 之前,各个feature map的相对位置在计算中一直不变。
因此,如果 f i f_i fi是位置 i i i处的特征向量,则 f i f_i fi将由对应于第 j j j个特征映射的块 f ( j ) f^{(j)} f(j)组成。线性分类器 w w w将类似地分解。 w w w和 f i f_i fi之间的点积可以写成:
w T f i = ∑ w ( j ) T f i ( j ) w^Tf_i = \sum w^{(j)T}f_i^{(j)} wTfi=∑w(j)Tfi(j)
分解中的第 j j j项对应于上采样第 j j j个feature map之上的线性分类器。 但是,由于上采样是线性运算,我们可以先应用分类器,然后使用公式1进行上采样:
f i ( j ) = ∑ k α i k ( j ) F k ( j ) f_i^{(j)} = \sum_k \alpha_{ik}^{(j)}F_k^{(j)} fi(j)=k∑αik(j)Fk(j)
w ( j ) f i ( j ) = ∑ k α i k ( j ) w ( j ) T F k ( j ) w^{(j)}f_i^{(j)} = \sum_k \alpha_{ik}^{(j)}w^{(j)T}F_k^{(j)} w(j)fi(j)=k∑αik(j)w(j)TFk(j)
观察到将分类器应用于feature map 中的每个位置与1×1卷积相同。因此,要在超列特征之上运行线性分类器,我们将其分解为与每个feature map相对应的块,在每feature map 上运行1×1卷积以生成分数图,将所有分数图上采样到目标分辨率,以及求和。
关于图2中,经过网格分类器后概率图是 50 × 50 × K 2 50\times 50 \times K^2 50×50×K2 的解释:
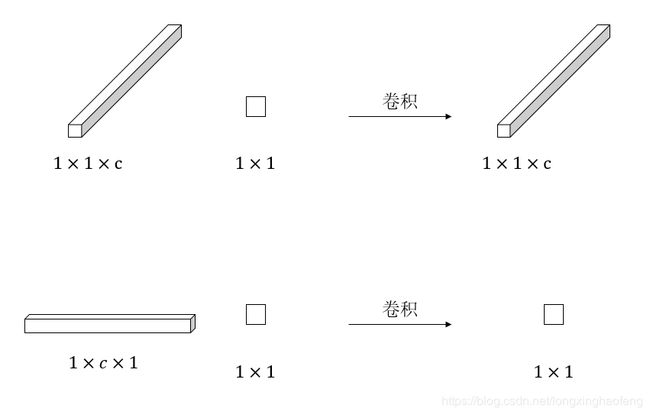
每一个网格分类器的作用类似 1 × 1 1 \times 1 1×1 的卷积,那么 f i f_i fi 是 1 × 1 1\times 1 1×1 ,经过卷积后是 1 × 1 × c 1\times 1\times c 1×1×c ,而论文中提到,网格中的每个分类器是一个函数 g k ( ⋅ ) g_k(·) gk(⋅),它接收一个特征向量并输出0到1之间的概率。所以针对 f i f_i fi 的分类器,计算过程应该是 1 × c × 1 1 \times c \times 1 1×c×1,经过卷积后结果是个标量。
考虑对该流水线的进一步修改,其中我们用一般的n×n卷积替换1×1卷积。
5、神经网络
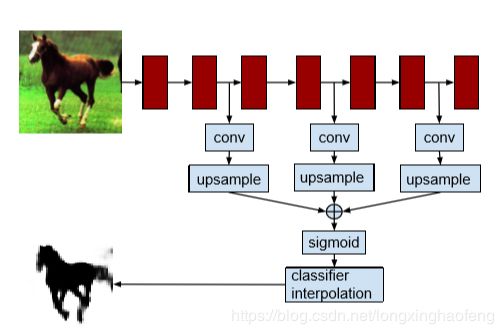
如图2所示。对于每个feature map,我们堆叠在一个额外的卷积层上。每个这样的卷积层都有 K 2 K^2 K2 个通道,对应我们想要训练的 K 2 K^2 K2 分类器。如上所述,我们可以为卷积选择任何内核大小,但对于生成1×1特征映射的完全连接的层,我们仅限于1×1卷积。我们获取所有这些层的输出,使用双线性插值对它们进行上采样并求它们。最后,我们通过sigmoid传递这些输出,并使用等式3组合 K 2 K^2 K2 feature map 以给出我们的最终输出。