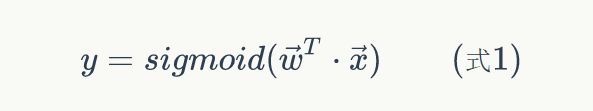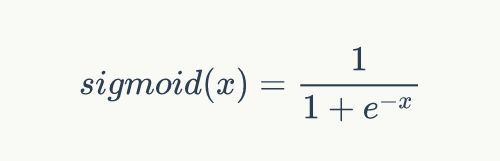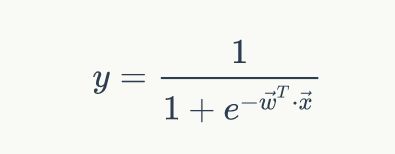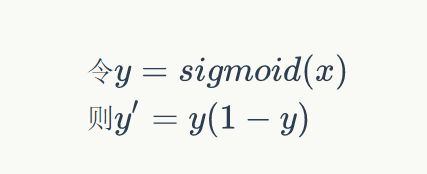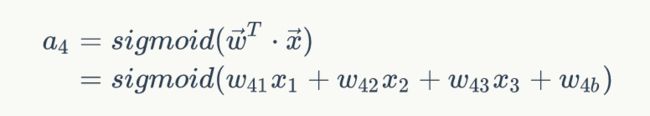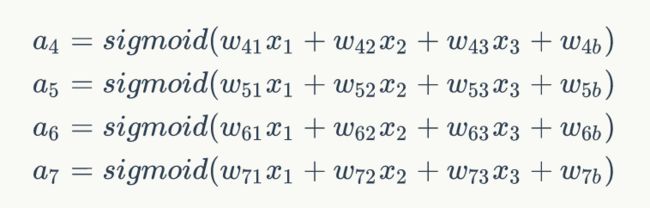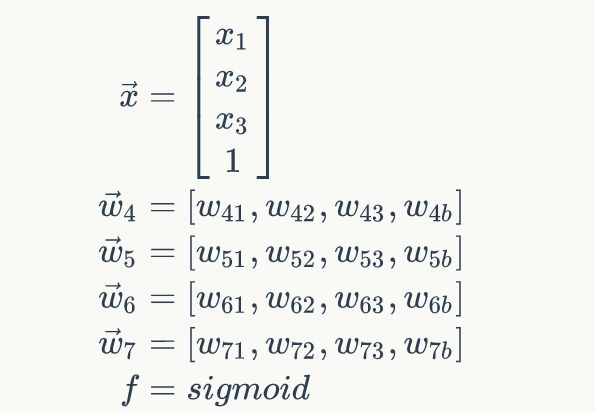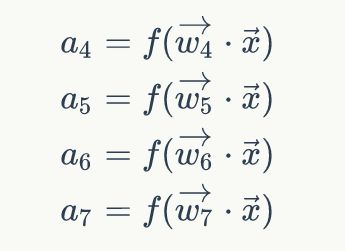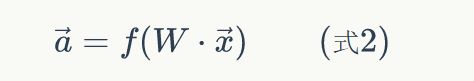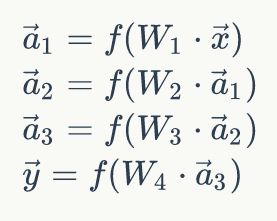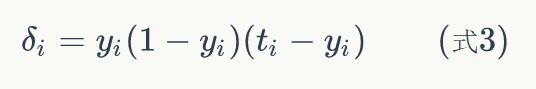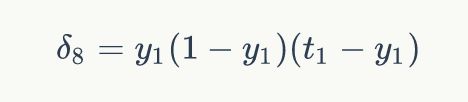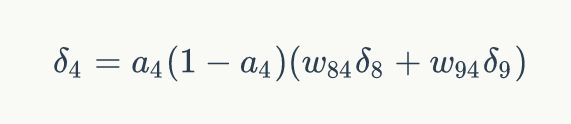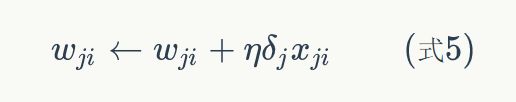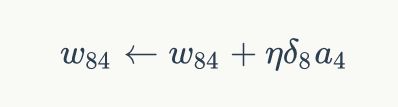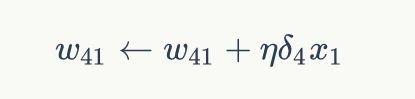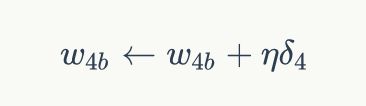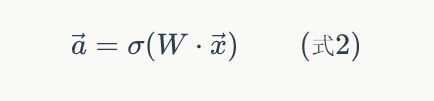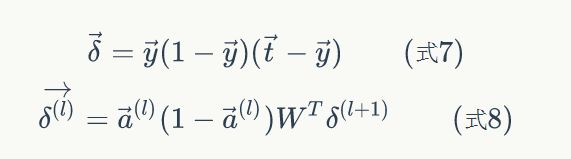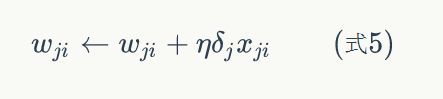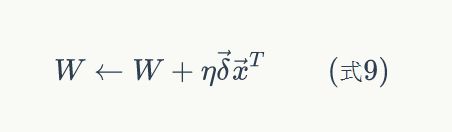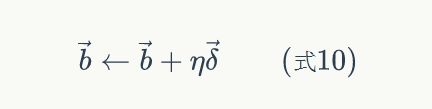零基础入门深度学习(3) - 神经网络和反向传播算法
python深度学习大全
原文地址:https://www.zybuluo.com/hanbingtao/note/476663
往期回顾
在上一篇文章中,我们已经掌握了机器学习的基本套路,对模型、目标函数、优化算法这些概念有了一定程度的理解,而且已经会训练单个的感知器或者线性单元了。在这篇文章中,我们将把这些单独的单元按照一定的规则相互连接在一起形成神经网络,从而奇迹般的获得了强大的学习能力。我们还将介绍这种网络的训练算法:反向传播算法。最后,我们依然用代码实现一个神经网络。如果您能坚持到本文的结尾,将会看到我们用自己实现的神经网络去识别手写数字。现在请做好准备,您即将双手触及到深度学习的大门。
神经元
神经元和感知器本质上是一样的,只不过我们说感知器的时候,它的激活函数是阶跃函数;而当我们说神经元时,激活函数往往选择为sigmoid函数或tanh函数。如下图所示:
计算一个神经元的输出的方法和计算一个感知器的输出是一样的。假设神经元的输入是向量![]() ,权重向量是
,权重向量是![]() (偏置项是w0),激活函数是sigmoid函数,则其输出y:
(偏置项是w0),激活函数是sigmoid函数,则其输出y:
sigmoid函数的定义如下:
将其带入前面的式子,得到
sigmoid函数是一个非线性函数,值域是(0,1)。函数图像如下图所示
sigmoid函数的导数是:
可以看到,sigmoid函数的导数非常有趣,它可以用sigmoid函数自身来表示。这样,一旦计算出sigmoid函数的值,计算它的导数的值就非常方便。
神经网络是啥
神经网络其实就是按照一定规则连接起来的多个神经元。上图展示了一个全连接(full connected, FC)神经网络,通过观察上面的图,我们可以发现它的规则包括:
- 神经元按照层来布局。最左边的层叫做输入层,负责接收输入数据;最右边的层叫输出层,我们可以从这层获取神经网络输出数据。输入层和输出层之间的层叫做隐藏层,因为它们对于外部来说是不可见的。
- 同一层的神经元之间没有连接。
- 第N层的每个神经元和第N-1层的所有神经元相连(这就是full connected的含义),第N-1层神经元的输出就是第N层神经元的输入。
- 每个连接都有一个权值。
上面这些规则定义了全连接神经网络的结构。事实上还存在很多其它结构的神经网络,比如卷积神经网络(CNN)、循环神经网络(RNN),他们都具有不同的连接规则。
计算神经网络的输出
神经网络实际上就是一个输入向量![]() 到输出向量
到输出向量![]() 的函数,即:
的函数,即:
根据输入计算神经网络的输出,需要首先将输入向量![]() 的每个元素xi的值赋给神经网络的输入层的对应神经元,然后根据式1依次向前计算每一层的每个神经元的值,直到最后一层输出层的所有神经元的值计算完毕。最后,将输出层每个神经元的值串在一起就得到了输出向量
的每个元素xi的值赋给神经网络的输入层的对应神经元,然后根据式1依次向前计算每一层的每个神经元的值,直到最后一层输出层的所有神经元的值计算完毕。最后,将输出层每个神经元的值串在一起就得到了输出向量![]() 。
。
接下来举一个例子来说明这个过程,我们先给神经网络的每个单元写上编号。
如上图,输入层有三个节点,我们将其依次编号为1、2、3;隐藏层的4个节点,编号依次为4、5、6、7;最后输出层的两个节点编号为8、9。因为我们这个神经网络是全连接网络,所以可以看到每个节点都和上一层的所有节点有连接。比如,我们可以看到隐藏层的节点4,它和输入层的三个节点1、2、3之间都有连接,其连接上的权重分别为w41,w42,w43。那么,我们怎样计算节点4的输出值a4呢?
为了计算节点4的输出值,我们必须先得到其所有上游节点(也就是节点1、2、3)的输出值。节点1、2、3是输入层的节点,所以,他们的输出值就是输入向量![]() 本身。按照上图画出的对应关系,可以看到节点1、2、3的输出值分别是x1,x2,x3。我们要求输入向量的维度和输入层神经元个数相同,而输入向量的某个元素对应到哪个输入节点是可以自由决定的,你偏非要把x1赋值给节点2也是完全没有问题的,但这样除了把自己弄晕之外,并没有什么价值。
本身。按照上图画出的对应关系,可以看到节点1、2、3的输出值分别是x1,x2,x3。我们要求输入向量的维度和输入层神经元个数相同,而输入向量的某个元素对应到哪个输入节点是可以自由决定的,你偏非要把x1赋值给节点2也是完全没有问题的,但这样除了把自己弄晕之外,并没有什么价值。
一旦我们有了节点1、2、3的输出值,我们就可以根据式1计算节点a4的输出值:
上式的是节点w4b的偏置项,图中没有画出来。而w41,w42,w43分别为节点1、2、3到节点4连接的权重,在给权重wji编号时,我们把目标节点的编号j放在前面,把源节点的编号i放在后面。
同样,我们可以继续计算出节点5、6、7的输出值a5,a6,a7。这样,隐藏层的4个节点的输出值就计算完成了,我们就可以接着计算输出层的节点8的输出值y1:
同理,我们还可以计算出y2的值。这样输出层所有节点的输出值计算完毕,我们就得到了在输入向量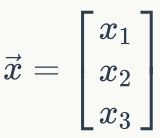 时,神经网络的输出向量
时,神经网络的输出向量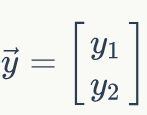 。这里我们也看到,输出向量的维度和输出层神经元个数相同。
。这里我们也看到,输出向量的维度和输出层神经元个数相同。
神经网络的矩阵表示
神经网络的计算如果用矩阵来表示会很方便(当然逼格也更高),我们先来看看隐藏层的矩阵表示。
首先我们把隐藏层4个节点的计算依次排列出来:
接着,定义网络的输入向量![]() 和隐藏层每个节点的权重向量
和隐藏层每个节点的权重向量![]() 。令
。令
代入到前面的一组式子,得到:
现在,我们把上述计算a1,a2,a3,a4的四个式子写到一个矩阵里面,每个式子作为矩阵的一行,就可以利用矩阵来表示它们的计算了。令
带入前面的一组式子,得到
在式2中,f是激活函数,在本例中是sigmoid函数;W是某一层的权重矩阵;![]() 是某层的输入向量;
是某层的输入向量;![]() 是某层的输出向量。式2说明神经网络的每一层的作用实际上就是先将输入向量左乘一个数组进行线性变换,得到一个新的向量,然后再对这个向量逐元素应用一个激活函数。
是某层的输出向量。式2说明神经网络的每一层的作用实际上就是先将输入向量左乘一个数组进行线性变换,得到一个新的向量,然后再对这个向量逐元素应用一个激活函数。
每一层的算法都是一样的。比如,对于包含一个输入层,一个输出层和三个隐藏层的神经网络,我们假设其权重矩阵分别为W1,W2,W3,W4,每个隐藏层的输出分别是![]() ,神经网络的输入为
,神经网络的输入为![]() ,神经网络的输入为
,神经网络的输入为![]() ,如下图所示:
,如下图所示:
则每一层的输出向量的计算可以表示为:
这就是神经网络输出值的计算方法。
神经网络的训练
现在,我们需要知道一个神经网络的每个连接上的权值是如何得到的。我们可以说神经网络是一个模型,那么这些权值就是模型的参数,也就是模型要学习的东西。然而,一个神经网络的连接方式、网络的层数、每层的节点数这些参数,则不是学习出来的,而是人为事先设置的。对于这些人为设置的参数,我们称之为超参数(Hyper-Parameters)。
接下来,我们将要介绍神经网络的训练算法:反向传播算法。
反向传播算法(Back Propagation)
我们首先直观的介绍反向传播算法,最后再来介绍这个算法的推导。当然读者也可以完全跳过推导部分,因为即使不知道如何推导,也不影响你写出来一个神经网络的训练代码。事实上,现在神经网络成熟的开源实现多如牛毛,除了练手之外,你可能都没有机会需要去写一个神经网络。
我们以监督学习为例来解释反向传播算法。在零基础入门深度学习(2) - 线性单元和梯度下降一文中我们介绍了什么是监督学习,如果忘记了可以再看一下。另外,我们设神经元的激活函数f为sigmoid函数(不同激活函数的计算公式不同)。
我们假设每个训练样本为![]() ,其中向量
,其中向量![]() 是训练样本的特征,而
是训练样本的特征,而![]() 是样本的目标值。
是样本的目标值。
首先,我们根据上一节介绍的算法,用样本的特征![]() ,计算出神经网络中每个隐藏层节点的输出ai,以及输出层每个节点的输出yi。
,计算出神经网络中每个隐藏层节点的输出ai,以及输出层每个节点的输出yi。
然后,我们按照下面的方法计算出每个节点的误差项![]() :
:
- 对于输出层节点i,
其中,![]() 是节点i的误差项,yi是节点i的输出值,ti是样本对应于节点i的目标值。举个例子,根据上图,对于输出层节点8来说,它的输出值是y1,而样本的目标值是t1,带入上面的公式得到节点8的误差项应该是
是节点i的误差项,yi是节点i的输出值,ti是样本对应于节点i的目标值。举个例子,根据上图,对于输出层节点8来说,它的输出值是y1,而样本的目标值是t1,带入上面的公式得到节点8的误差项应该是![]() :
:
- 对于隐藏层节点,
其中,ai是节点i的输出值,wki是节点i到它的下一层节点k的连接的权重,![]() 是节点i的下一层节点k的误差项。例如,对于隐藏层节点4来说,计算方法如下:
是节点i的下一层节点k的误差项。例如,对于隐藏层节点4来说,计算方法如下:
最后,更新每个连接上的权值:
其中,wji是节点i到节点j的权重,![]() 是一个成为学习速率的常数,
是一个成为学习速率的常数,![]() 是节点j的误差项,xji是节点i传递给节点j的输入。例如,权重w84的更新方法如下:
是节点j的误差项,xji是节点i传递给节点j的输入。例如,权重w84的更新方法如下:
类似的,权重w41的更新方法如下:
偏置项的输入值永远为1。例如,节点w4b的偏置项应该按照下面的方法计算:
我们已经介绍了神经网络每个节点误差项的计算和权重更新方法。显然,计算一个节点的误差项,需要先计算每个与其相连的下一层节点的误差项。这就要求误差项的计算顺序必须是从输出层开始,然后反向依次计算每个隐藏层的误差项,直到与输入层相连的那个隐藏层。这就是反向传播算法的名字的含义。当所有节点的误差项计算完毕后,我们就可以根据式5来更新所有的权重。
以上就是基本的反向传播算法,并不是很复杂,您弄清楚了么?
反向传播算法的推导
反向传播算法其实就是链式求导法则的应用。具体不再详述,有兴趣可以参考https://www.zybuluo.com/hanbingtao/note/476663#an1
超参数的确定
在实现网络模型训练前,我们首先需要确定网络的层数和每层的节点数。关于第一个问题,实际上并没有什么理论化的方法,大家都是根据经验来拍,如果没有经验的话就随便拍一个。然后,你可以多试几个值,训练不同层数的神经网络,看看哪个效果最好就用哪个。嗯,现在你可能明白为什么说深度学习是个手艺活了,有些手艺很让人无语,而有些手艺还是很有技术含量的。
不过,有些基本道理我们还是明白的,我们知道网络层数越多越好,也知道层数越多训练难度越大。对于全连接网络,隐藏层最好不要超过三层。那么,我们可以先试试仅有一个隐藏层的神经网络效果怎么样。毕竟模型小的话,训练起来也快些(刚开始玩模型的时候,都希望快点看到结果)。
输入层节点数一般是确定的,它是我们能提供的特征数目。输出层节点数也是确定的,也就是我们所区分的分类数目。输出节点,每个节点对应一个分类。输出最大值的那个节点对应的分类,就是模型的预测结果。
隐藏层节点数量是不好确定的,从1到100万都可以。下面有几个经验公式:
向量化编程
我们用向量化编程的方法,实现前面的全连接神经网络。
首先,我们需要把所有的计算都表达为向量的形式。对于全连接神经网络来说,主要有三个计算公式。
前向计算,我们发现式2已经是向量化的表达了:
上式中的![]() 表示sigmoid函数。
表示sigmoid函数。
反向计算,我们需要把式3和式4使用向量来表示:
我们还需要权重数组W和偏置项b的梯度计算的向量化表示。也就是需要把式5使用向量化表示:
其对应的向量化表示为:
更新偏置项的向量化表示为:
在使用向量化编程中最重要的库莫过于numpy库。
1. 当为array的时候,默认d*f就是对应元素的乘积,multiply也是对应元素的乘积,dot(d,f)会转化为矩阵的乘积。
2. 当为mat的时候,默认d*f就是矩阵的乘积,multiply转化为对应元素的乘积,dot(d,f)为矩阵的乘积。
现在,我们根据上面几个公式,重新实现一个类:FullConnectedLayer。它实现了全连接层的前向和后向计算:
# 全连接每层的实现类。输入对象x、神经层输出a、输出y均为列向量
class FullConnectedLayer(object):
# 构造函数。input_size: 本层输入向量的维度。output_size: 本层输出向量的维度。activator: 激活函数
def __init__(self, input_size, output_size,activator):
self.input_size = input_size
self.output_size = output_size
self.activator = activator
# 权重数组W
self.W = np.random.uniform(-0.1, 0.1,(output_size, input_size)) #初始化为-0.1~0.1之间的数。权重的大小。行数=输出个数,列数=输入个数。a=w*x,a和x都是列向量
# 偏置项b
self.b = np.zeros((output_size, 1)) # 全0列向量偏重项
# 输出向量
self.output = np.zeros((output_size, 1)) #初始化为全0列向量
# 前向计算,预测输出。input_array: 输入向量,维度必须等于input_size
def forward(self, input_array): # 式2
self.input = input_array
self.output = self.activator.forward(np.dot(self.W, input_array) + self.b)
# 反向计算W和b的梯度。delta_array: 从上一层传递过来的误差项。列向量
def backward(self, delta_array):
# 式8
self.delta = np.multiply(self.activator.backward(self.input),np.dot(self.W.T, delta_array)) #计算当前层的误差,已被上一层使用
self.W_grad = np.dot(delta_array, self.input.T) # 计算w的梯度。梯度=误差.*输入
self.b_grad = delta_array #计算b的梯度
# 使用梯度下降算法更新权重
def update(self, learning_rate):
self.W += learning_rate * self.W_grad
self.b += learning_rate * self.b_grad现在,我们再实验Network类,使之用到FullConnectedLayer:
# Sigmoid激活函数类
class SigmoidActivator(object):
def forward(self, weighted_input): #前向传播计算输出
return 1.0 / (1.0 + np.exp(-weighted_input))
def backward(self, output): #后向传播计算w和b的梯度
return np.multiply(output,(1 - output)) # 对应元素相乘
# 神经网络类
class Network(object):
# 初始化一个全连接神经网络。layers:数组,描述神经网络每层节点数。包含输入层节点个数、隐藏层节点个数、输出层节点个数
def __init__(self, layers):
self.layers = []
for i in range(len(layers) - 1):
self.layers.append(FullConnectedLayer(layers[i], layers[i+1],SigmoidActivator())) # 创建全连接层,并添加到layers中
# 训练函数。labels: 样本标签矩阵。data_set: 输入样本矩阵。rate: 学习速率。epoch: 训练轮数
def train(self, labels, data_set, rate, epoch):
for i in range(epoch):
for d in range(len(data_set)):
self.train_one_sample(labels[d].reshape(-1,1),data_set[d].reshape(-1,1), rate) #将输入对象和输出标签转化为列向量
# 内部函数,用一个样本训练网络
def train_one_sample(self, label, sample, rate):
# print('样本:\n',sample)
self.predict(sample) # 根据样本对象预测值
self.calc_gradient(label) # 计算梯度
self.update_weight(rate) # 更新权重
# 使用神经网络实现预测。sample: 输入样本
def predict(self, sample):
sample = sample.reshape(-1,1) #将样本转换为列向量
output = sample # 输入样本作为输入层的输出
for layer in self.layers:
# print('权值:',layer.W,layer.b)
layer.forward(output) # 逐层向后计算预测值。因为每层都是线性回归
output = layer.output
# print('预测输出:', output)
return output
# 内部函数,计算每个节点的误差。label为一个样本的输出向量,也就对应了最后一个所有输出节点输出的值
def calc_gradient(self, label):
# print('计算梯度:',self.layers[-1].activator.backward(self.layers[-1].output).shape)
delta = np.multiply(self.layers[-1].activator.backward(self.layers[-1].output),(label - self.layers[-1].output)) #计算输出误差
# print('输出误差:', delta.shape)
for layer in self.layers[::-1]:
layer.backward(delta) # 逐层向前计算误差。计算神经网络层和输入层误差
delta = layer.delta
# print('当前层误差:', delta.shape)
return delta
# 内部函数,更新每个连接权重
def update_weight(self, rate):
for layer in self.layers: # 逐层更新权重
layer.update(rate)
现在,我们来实现一个and运算。
#由于使用了逻辑回归函数,所以只能进行分类识别。识别ont-hot编码的结果
if __name__ == '__main__':
# 使用神经网络实现and运算
data_set = np.array([[0,0],[0,1],[1,0],[1,1]])
labels = np.array([[1,0],[1,0],[1,0],[0,1]])
# print(data_set)
# print(labels)
net = Network([2,1,2]) # 输入节点2个(偏量b会自动加上),神经元1个,输出节点2个。
net.train(labels, data_set, 2, 100)
for layer in net.layers: # 网络层总不包含输出层
print('W:',layer.W)
print('b:',layer.b)
# 对结果进行预测
sample = np.mat([[0,1]])
y = net.predict(sample)
print(y)小结
至此,你已经完成了又一次漫长的学习之旅。你现在应该已经明白了神经网络的基本原理,高兴的话,你甚至有能力去动手实现一个,并用它解决一些问题。如果感到困难也不要气馁,这篇文章是一个重要的分水岭,如果你完全弄明白了的话,在真正的『小白』和装腔作势的『大牛』面前吹吹牛是完全没有问题的。
作为深度学习入门的系列文章,本文也是上半场的结束。在这个半场,你掌握了机器学习、神经网络的基本概念,并且有能力去动手解决一些简单的问题(例如手写数字识别,如果用传统的观点来看,其实这些问题也不简单)。而且,一旦掌握基本概念,后面的学习就容易多了。
在下半场,我们讲介绍更多『深度』学习的内容,我们已经讲了神经网络(Neutrol Network),但是并没有讲深度神经网络(Deep Neutrol Network)。Deep会带来更加强大的能力,同时也带来更多的问题。如果不理解这些问题和它们的解决方案,也不能说你入门了『深度』学习。
目前业界有很多开源的神经网络实现,它们的功能也要强大的多,因此你并不需要事必躬亲的去实现自己的神经网络。我们在上半场不断的从头发明轮子,是为了让你明白神经网络的基本原理,这样你就能非常迅速的掌握这些工具。在下半场的文章中,我们改变了策略:不会再去从头开始去实现,而是尽可能应用现有的工具。
下一篇文章,我们介绍不同结构的神经网络,比如鼎鼎大名的卷积神经网络,它在图像和语音领域已然创造了诸多奇迹,在自然语言处理领域的研究也如火如荼。某种意义上说,它的成功大大提升了人们对于深度学习的信心。