波士顿房价问题——多元线性回归+TensorFlow

波士顿房价问题——多元线性回归+Tensorflow

决定房价的因素有很多，所以采用多元线性回归模型


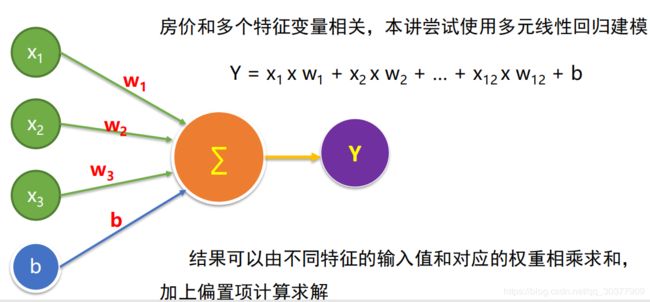
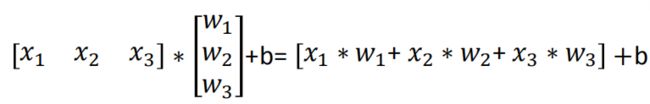
官方提供的波士顿房价项目数据集

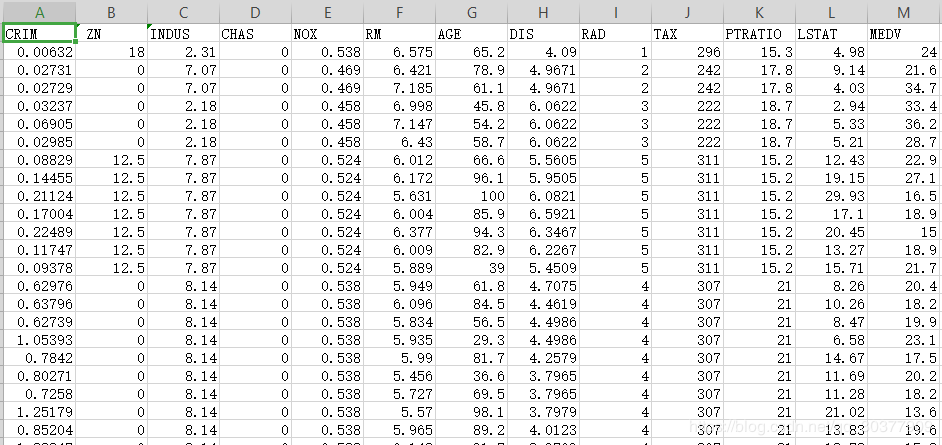
其中，
载入数据

df = pd.read_csv('boston.csv', header=0)

观察数据摘要描述信息

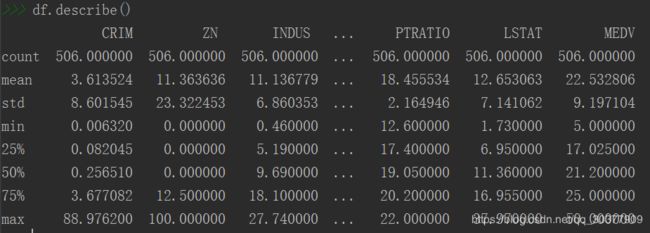
将df转换为np的数组格式,并做归一化
归一化：（特征值-特征最小值）/(特征最大值-特征最小值）
如果缺少归一化步骤，不同特征值的取值范围大小不同，可能会导致利用梯度下降法训练的结果异常，可能返回的值都是缺失值。

#获取df的值
df = df.values
#转换为np的数组格式
df = np.array(df)
#对特征数据【0到11】列做（0-1）归一化
for i in range(12):
    df[:, i] = df[:, i]/(df[:, i].max() - df[:, i].min())

前11列数据为特征数据，最后一列平均房价为标签数据

x_data = df[:, :12]
y_data = df[:, 12]

开始建模

#定义一个命名空间
with tf.name_scope('Model'):
    #w 初始化值为shape=（12,1）的随机数
    w = tf.Variable(tf.random_normal([12, 1], stddev=0.01, name='W'))
    #b 初始化值为1.0
    b = tf.Variable(1.0, name='b')
    #w和x是矩阵相乘，用matmul，不能用mutiply或*
    def model(x, w, b):
        return tf.matmul(x, w) + b
    #预测计算操作，前向计算节点
    pred = model(x, w, b)

设置训练超参数

train_epochs = 50
learning_rate = 0.01
#定义均方差损失函数
with tf.name_scope('LossFunction'):
    loss_function = tf.reduce_mean(tf.pow(y-pred, 2))
#定义优化器
optimizer = tf.train.GradientDescentOptimizer(learning_rate).minimize(loss_function)

声明会话

sess = tf.Session()
#初始化变量
init = tf.global_variables_initializer()

启动会话

sess.run(init)

模型训练

for epoch in range(train_epochs):
    loss_sum = 0.0
    for xs, ys in zip(x_data, y_data):
        #数据变形，要和placeholder的shape保持一致
        xs = xs.reshape(1, 12)
        ys = ys.reshape(1, 1)
        _, loss = sess.run([optimizer, loss_function], feed_dict={x:xs, y:ys})
        #_, summary_str, loss = sess.run([optimizer, sum_loss_op, loss_function], feed_dict={x: xs, y: ys})
        writer.add_summary(summary_str, epoch)
        #计算本轮loss值得和
        loss_sum = loss_sum + loss
    #打乱数据顺序
    xvalues, yvalues = shuffle(x_data, y_data)

    b0temp = b.eval(session=sess)
    w0temp = w.eval(session=sess)
    loss_average = loss_sum/len(y_data)

    #loss_list.append(loss_average)#每轮添加一次
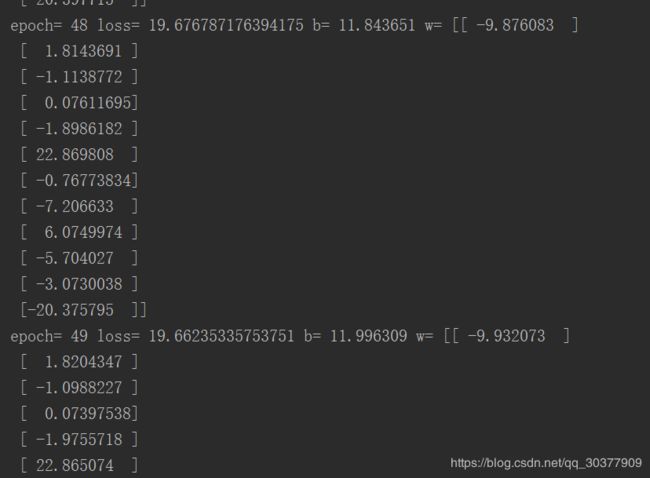
    print('epoch=', epoch+1, 'loss=', loss_average, 'b=', b0temp, 'w=', w0temp)

注：zip:接受任意多个（包括0个和1个）序列作为参数，返回一个tuple列表。
shuffle() :将序列的所有元素随机排序
eval():将字符串string对象转化为有效的表达式参与求值运算返回计算结果

观察结果

验证：

n = np.random.randint(506)#一共506条数据
print(n)
x_test = x_data[n]
x_test = x_test.reshape(1, 12)
predict = sess.run(pred, feed_dict={x: x_test})
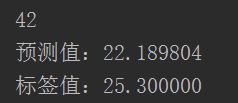
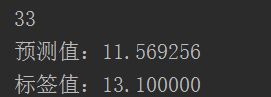
print('预测值：%f' % predict)
target = y_data[n]
print('标签值：%f' % target)

至此，波士顿房价预测问题的代码完成。

完善：可视化过程

为tensorboard可视化准备数据

给每步训练后添加一个该步的Loss值

可视化损失值

plt.plot(loss_list)
plt.show()

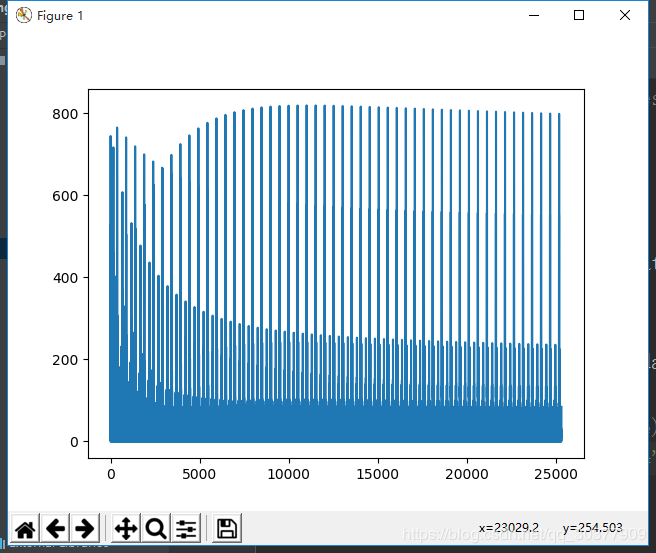
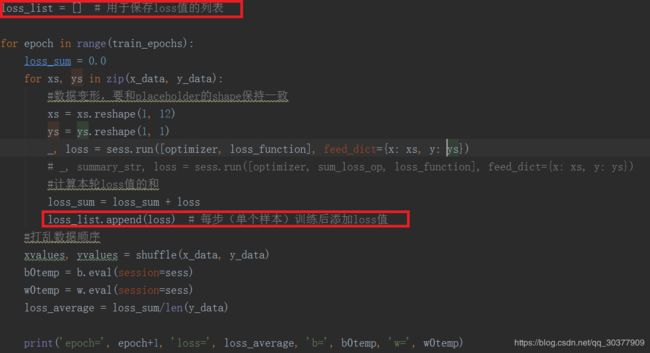
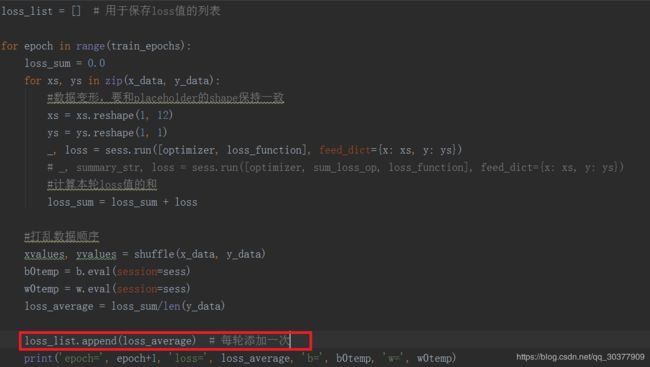
或者将loss设置为每轮添加一次Loss的平均值，而不是每一步


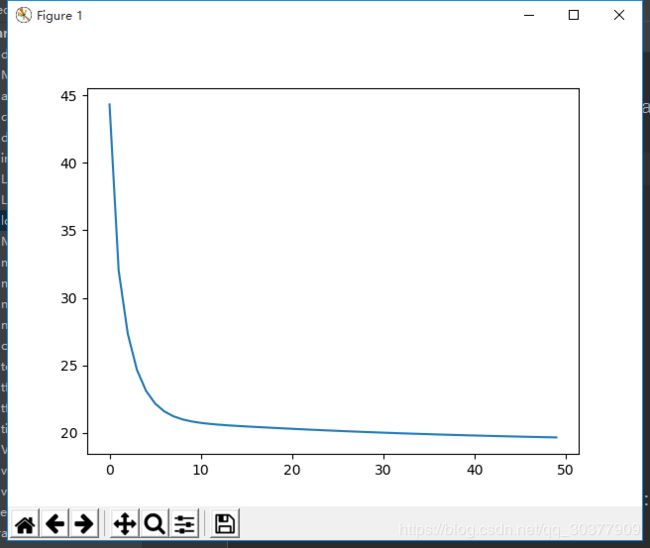
加上tensorboard可视化代码
原先声明会话的代码修改为：

sess = tf.Session()
#定义初始化变量
init = tf.global_variables_initializer()

#设置日志存储目录
logdir='#自己的存储目录'
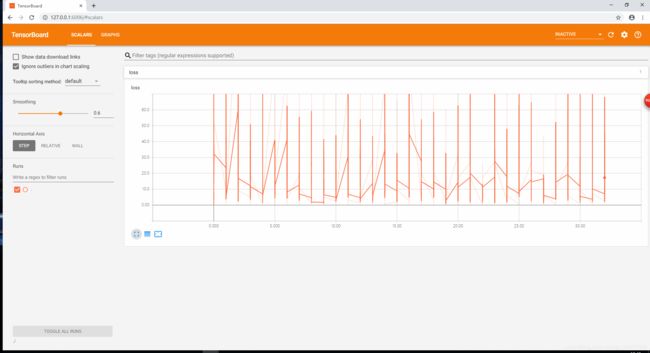
#创建一个操作，记录损失值loss，后面在tensorboard中SCALARS栏可见
sum_loss_op = tf.summary.scalar('loss', loss_function)
#把所有需要记录摘要日志文件的合并，方便一次性写入
merged = tf.summary.merge_all()

sess.run(init)
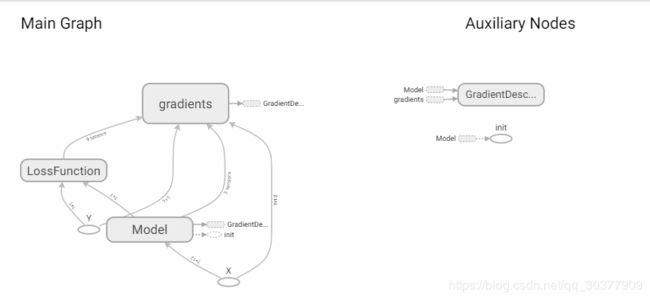
# 创建摘要writer，将计算图写入摘要文件，后面在tensorboard中GRAPHS栏可见
writer = tf.summary.FileWriter(logdir, sess.graph)

训练过程的代码做一些修改

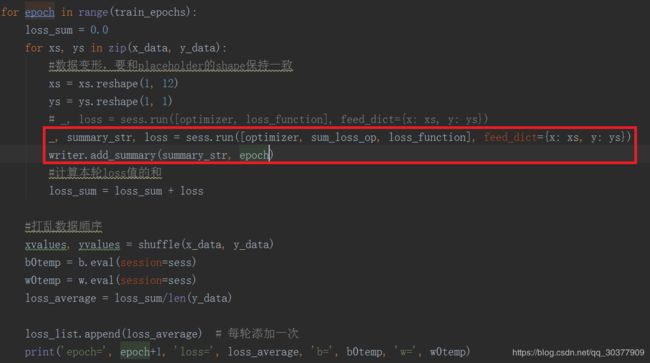
如何打开tensorboard观察可以参考这篇博客：
https://blog.csdn.net/qq_30377909/article/details/89946818


结束