动态规划5：编辑距离算法（Edit Distance）

#概念

编辑距离的作用主要是用来比较两个字符串的相似度的

基本的定义如下所示：

编辑距离，又称Levenshtein距离（莱文斯坦距离也叫做Edit Distance），是指两个字串之间，由一个转成另一个所需的最少编辑操作次数，如果它们的距离越大，说明它们越是不同。许可的编辑操作包括将一个字符替换成另一个字符，插入一个字符，删除一个字符。

这个概念是由俄罗斯科学家Vladimir Levenshtein在1965年提出来的，所以也叫 Levenshtein 距离。它可以用来做DNA分析，拼字检测，抄袭识别等等。总是比较相似的，或多或少我们可以考虑编辑距离。

在概念中，我们可以看出一些重点那就是，编辑操作只有三种。插入，删除，替换这三种操作，我们有两个字符串，将其中一个字符串经过上面的这三种操作之后，得到两个完全相同的字符串付出的代价是什么就是我们要讨论和计算的。

例如：
我们有两个字符串： kitten 和 sitting:
现在我们要将kitten转换成sitting
我们可以做如下的一些操作；

k i t t e n --> s i t t e n 将K替换成S

sitten --> sittin 将 e 替换成i

sittin --> sitting 添加g

在这里我们设置每经过一次编辑，也就是变化（插入，删除，替换）我们花费的代价都是1。

例如：

• 如果str1=“ivan”，str2=“ivan”，那么经过计算后等于 0。没有经过转换。相似度=1-0/Math.Max(str1.length,str2.length)=1

• 如果str1=“ivan1”，str2=“ivan2”，那么经过计算后等于1。str1的"1"转换"2"，转换了一个字符，所以距离是1，相似度=1-1/Math.Max(str1.length,str2.length)=0.8

---

---

#算法过程

1.str1或str2的长度为0返回另一个字符串的长度。 if(str1.length0) return str2.length; if(str2.length0) return str1.length;

2.初始化(n+1)(m+1)的矩阵d，并让第一行和列的值从0开始增长。扫描两字符串（nm级的），如果：str1[i] == str2[j]，用temp记录它，为0。否则temp记为1。然后在矩阵d[i,j]赋于d[i-1,j]+1 、d[i,j-1]+1、d[i-1,j-1]+temp三者的最小值。

3.扫描完后，返回矩阵的最后一个值d[n][m]即是它们的距离。

计算相似度公式：1-它们的距离/两个字符串长度的最大值。

---

其实这个算法并不难实现
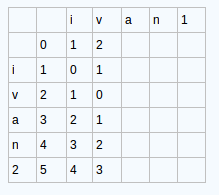
我们用字符串“ivan1”和“ivan2”举例来看看矩阵中值的状况：

1、第一行和第一列的值从0开始增长

图一

首先我们先创建一个矩阵，或者说是我们的二维数列，假设有两个字符串，我们的字符串的长度分别是m和n，那么，我们矩阵的维度就应该是(m+1)*(n+1).

注意，我们先给数列的第一行第一列赋值，从0开始递增赋值。我们就得到了图一的这个样子

之后我们计算第一列，第二列，依次类推，算完整个矩阵。

我们的计算规则就是：
d[i,j]=min(d[i-1,j]+1 、d[i,j-1]+1、d[i-1,j-1]+temp) 这三个当中的最小值。

其中：str1[i] == str2[j]，用temp记录它，为0。否则temp记为1

我们用d[i-1,j]+1表示增加操作
d[i,j-1]+1 表示我们的删除操作
d[i-1,j-1]+temp表示我们的替换操作

2、举证元素的产生 Matrix[i - 1, j] + 1 ; Matrix[i, j - 1] + 1 ; Matrix[i - 1, j - 1] + t 三者当中的最小值

3.依次类推直到矩阵全部生成

这个就得到了我们的整个完整的矩阵。

算法分析：

也就是说，就是将一个字符串变成另外一个字符串所用的最少操作数，每次只能增加、删除或者替换一个字符。
首先我们令word1和word2分别为：michaelab和michaelxy（为了理解简单，我们假设word1和word2字符长度是一样的），dis[i][j]作为word1和word2之间的Edit Distance，我们要做的就是求出michaelx到michaely的最小steps。

首先解释下dis[i][j]：它是指word1[i]和word2[j]的Edit Distance。dis[0][0]表示word1和word2都为空的时候，此时他们的Edit Distance为0。很明显可以得出的，dis[0][j]就是word1为空，word2长度为j的情况，此时他们的Edit Distance为j，也就是从空，添加j个字符转换成word2的最小Edit Distance为j；同理dis[i][0]就是，word1长度为i，word2为空时，word1需要删除i个字符才能转换成空，所以转换成word2的最小Edit Distance为i。下面及时初始化代码：

下面来分析下题目规定的三个操作：添加，删除，替换。
假设word1[i]和word2[j](此处i = j)分别为：michaelab和michaelxy
如果b == y,
那么：dis[i][j] = dis[i-1][j-1]。
如果b!=y，
那么：添加：也就是在michaelab后面添加一个y，那么word1就变成了michaelaby，
此时 dis[i][j] = 1 + dis[i][j-1]；
上式中，1代表刚刚的添加操作，添加操作后，word1变成michaelaby，word2为michaelxy。
dis[i][j-1]代表从word1[i]转换成word2[j-1]的最小Edit Distance，也就是michaelab转换成michaelx的最小
Edit Distance，由于两个字符串尾部的y==y，所以只需要将michaelab变成michaelx就可以了，而他们之间的最
小Edit Distance就是dis[i][j-1]。

删除：也就是将michaelab后面的b删除，那么word1就变成了michaela，此时dis[i][j] = 1 + dis[i-1][j]；
上式中，1代表刚刚的删除操作，删除操作后，word1变成michaela，word2为michaelxy。dis[i-1][j]代表从
word[i-1]转换成word[j]的最小Edit Distance，也就是michaela转换成michaelxy的最小Edit Distance，所以
只需要将michaela变成michaelxy就可以了，而他们之间的最小Edit Distance就是dis[i-1][j]。

替换：也就是将michaelab后面的b替换成y，那么word1就变成了michaelay，此时dis[i][j] = 1 + dis[i-1][j-1]；
上式中，1代表刚刚的替换操作，替换操作后，word1变成michaelay，word2为michaelxy。dis[i-1][j-1]代表从
word[i-1]转换成word[j-1]的最小Edit Distance，也即是michaelay转换成michaelxy的最小Edit Distance，由
于两个字符串尾部的y==y，所以只需要将michaela变成michaelx就可以了，而他们之间的最小Edit Distance就是
dis[i-1][j-1]。

下面我们来看下代码：

public class LevenshteinDistance{
	private static int LowerOfThree(int first, int second, int third) {
		int min = Math.min(first, second);
        return Math.min(min, third);
    }

    private static int Levenshtein_Distance(String str1, String str2){
        int n = str1.length();
        int m = str2.length();
        int[][] Matrix = new int[n+1][m+1];
        int temp = 0;
        char ch1,ch2;
        int i,j;
        if(n == 0 || m == 0)  {
            return m;
        }
        for (i=0; i<=n; i++) {
            Matrix[i][0] = i; //初始化第一列
        }
        for (j=0; j <= m; j++){
            Matrix[0][j] = j; //初始化第一行
        }
        for (i=1; i <= n; i++){
            ch1 = str1.charAt(i-1);
            for (j=1; j <= m; j++){
               ch2 = str2.charAt(j-1);
               if (ch1 == ch2){
                    temp = 0;
                } else {
                    temp = 1;
                }
                Matrix[i][j] = LowerOfThree(Matrix[i-1][j]+1,Matrix[i][j-1]+1,Matrix[i-1][j-1]+temp);
            }
        }
        System.out.println(Matrix[n][m]);
        return Matrix[n][m];
    }
    public static void main(String[] args) {
		String str1 = "ivan1";
        String str2 = "ivan2";
        new LevenshteinDistance().Levenshtein_Distance(str1, str2);          
	}  
}

参考文献：

http://www.cnblogs.com/ivanyb/archive/2011/11/25/2263356.html

https://blog.csdn.net/Grace_0642/article/details/53944188

https://blog.csdn.net/baodream/article/details/80417695