模式匹配算法KMP
KMP算法对BF算法做了很大改进,是由克努特(Knuth),莫里斯(Morris),普拉特(Pratt)同时发现。
BF算法:
简单的模式匹配方法简称为BF算法。
假设m,n是两个串,m为主串,n为子串。在m中找到等于n的子串,则匹配成功,函数返回子串在主串首次出现的存储位置,否则匹配失败。(申明:本算法中字符串采用定长顺序存储,串的长度参数存放在0单元,串值从单元1开始存储,字符序号与存储位置一致)
简单实例如下:
m:aacbcbaadbcbba
n:cbaa
用子串n的第一个字符与主串m中的字符挨个对比,直到找到相同的字符,之后挨个比较是否相同,如果全都相同,那么匹配成功,如果出现不相同的字符那么再循环以上过程。
实例步骤如下:
第一趟:aacbcbaadbcbba(子串首字符在主串中挨个比较)了l
cbaa
第二趟:aacbcbaadbcbba(上一趟比较不成功,则比较后一个字符)
cbaa
第三趟:aacbcbaadbcbba(比较成功,挨个比较后面的字符是否也相同)
cbaa
第四趟:aacbcbaadbcbba
cbaa
第五趟:aacbcbaadbcbba(后面的字符出现不行同的,则再次用子串首字符在主串中比较)
cbaa
第六趟:aacbcbaadbcbba
cbaa
第七趟:aacbcbaadbcbba
cbaa
第八趟:aacbcbaadbcbba
cbaa
第九趟:aacbcbaadbcbba
cbaa
第十趟:aacbcbaadbcbba(循环以上过程,最终找到匹配的子串)
cbaa
C语言实现如下:
int Search_Chuan(char m[],char n[])//模式匹配BF算法,主串m,子串n
{
int i,j,k;
for (i=1;i<=m[0];i++)
{
j=1;//在找到相同字符之前,一直是子串的首字符与主串比较
if (m[i]==n[j])
{
for (k=i;k<=m[0],j<=n[0];k++,j++)
{
if (m[k]!=n[j])
{
break;
}
}
if (j==n[0]+1)//两种出循环的状态,正常循环结束j指向子串末尾,非正常出循环j不会指向子串末尾
{
return i;
}
}
}
return 0;
}例如:在上面的实例中
第四趟:aacbcbaadbcbba
cbaa
第五趟:aacbcbaadbcbba
cbaa
第六趟:aacbcbaadbcbba
cbaa
第五趟匹配失败后,回溯到首字符匹配成功位置的下一位置,第五趟表明子串前半部分cb是匹配的,所以回溯后首字符c必定再次与已知不匹配的b再比较一次,所以第六趟是不必要的,KMP算法最大程度的避免了这样的回溯,提高了运行效率。
KMP算法:
综上所述,在上述实例中我们希望在匹配失败之后,不回溯,子串首字符比较的位置向后划,跳过已知不会匹配成功的b字符。观察上述实例可以发现,当子串中有相同字符段或相同字符时,若这一段字符已经匹配成功,那我们就知道主串上的相同位置的字符,我们希望利用这个已知信息来避免回溯。
现在解决问题的关键在于比较的位置向后移动多少,在用实例进行推导时可以发现(这里不再引入实例,有兴趣可以自行研究),子串向后划动的长度与子串有关,这个算法的关键就是确定上述关系,问题的数学模型建立如下。
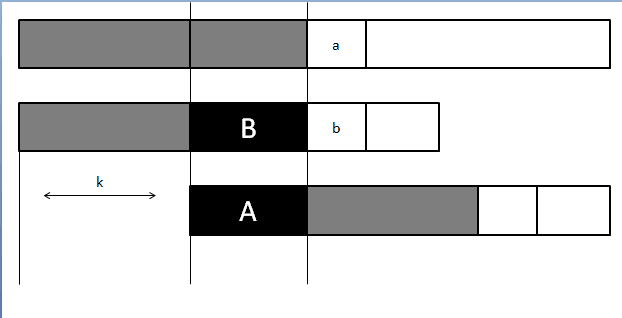
设主串下标为i,子串下标为j,子串划动的最终位置为k,那么k位置之前的字符段是相匹配的,所以有以下关系式成立
“n1,n2,n3,n4......nk-1”=“mi-k+1,mi-k+2,mi-k+3......mi-1”①
等号左边是子串在主串中相匹配的字符段,等号右边是匹配字符段在主串中的位置。
匹配失败是在nj和mi处,所以得到的部分匹配结果为:
“n1,n2,n3,n4......nj-1”=“mi-j+1,mi-j+2,mi-j+3......mi-1”②
因为k “nj-k+1,nj-k+2,nj-k+3......nj-1”=“mi-k+1,mi-k+2,mi-k+3......mi-1”③ 等号左边为子串的前k-1项,等号右边为主串的前k-1项 由①和③得: “n1,n2,n3,n4......nk-1”=“nj-k+1,nj-k+2,nj-k+3......nj-1”④ 结论:当在mi,nj时匹配失败,如果子串满足④式,那么子串n可以向右划动至nk位置与主串对准,再继续匹配。 上述过程实在太过于晦涩难懂了(我自己也是用实例推导了很多遍才勉强理解),并且很难理清(子串向后划动的长度与子串有关)这个关系,下面我引入另一个研究过程和方法。 下面先解释几个词汇: 字符串前缀:一个字符串除了最后一个字符以外,其前面所有字符组成的字符串的所有子字符串的集合 字符串:btboay 字符串前缀:“[b],[bt],[btb],[btbo],[btboa]” 字符串后缀:一个字符串除了第一个字符以外,其后面所有字符组成的字符串的所有子字符串的集合 字符串:btboay 字符串后缀:“[t],[tb],[tbo],[tboa],[tboay]” 部分匹配字符段:主串与子串相匹配的一段字符 主字符串:btboay 子字符串:boy 部分匹配字符段:bo btboay boy 部分匹配值:字符串的前缀和后缀最长的共有元素长度 字符串:btboay,其子字符串的部分匹配值为 ——“b”的前缀和后缀都为空集,共有元素长度为0 ——“bt”的前缀为[b],后缀为[t],共有元素长度为0 ——“btb”的前缀为[b,bt],后缀为[tb,b],共有元素长度为1 ——“btbo”的前缀为[b,bt,btb],后缀为[tbo,bo,o],共有元素长度为0 ——“btboa”的前缀为[b,bt,btb,btbo],后缀为[tboa,boa,oa,a],共有元素长度为0 ——“btboay”的前缀为[b,bt,btb,btbo,btboa],后缀为[tboay,boay,oay,ay,y],共有元素长度为0 移动位数=已匹配字符数-对应的部分匹配值 了解以上的基本概念后,下面列举几个实例来解释上面的计算式的由来: 实例一: 主串m:abcdeabcdf 子串n :abcdf 我们知道按照BF算法的思想,在比较到f处中断: abcdeabcdf abcdf 子串后移一位: abcdeabcdf abcdf 但实际上我们可以将子串直接移到这里: abcdeabcdf abcdf 为什么我们敢确定前面的字符不会出现匹配的情况:在第一轮的匹配中前面的abcd字符是匹配的,很明显这中间不可能有字符与首字符a相匹配,那是不是我们直接将子串移到下一个出现首字符a的地方就可以呢? 请看下面的例子: 实例二: 主串m:abadeabadf 子串n :abadf 第一轮失败: abadeabadf abadf 子串移到下一个出现a(与子串首字符相同)的地方: abadeabadf abadf 这样是可以的,简化了BF算法,但这样是最佳吗?在首轮匹配失败后,已知匹配成功的字符为abad,在上述移动后,我们发现,其实我们已经知道第二个a后面是d,与b是不匹配的。 可以直接移动到这里: abadeababf ababf 看完这两个例子,有人会想是不是直接移到匹配失败的位置就好了?(呵呵,不要犯傻) 再看下面的例子: 实例三: 主串m:ababeababf 子串n: ababf 在字符f处匹配失败后,子串可以直接移到这里: ababeababf ababf 主串m:abababf 子串n: ababf 在字符f处匹配失败后,子串可以直接移到这里: abababf ababf 实例三的结果可以发现移动后有一些规律,可以用下图来表示: 可以看到在已匹配的字符中A,B段是相同的,而这是已匹配字符段的后缀和前缀的最长共有元素(也就是部分匹配段),而子字符串移动位数k=已匹配字符长度-部分匹配值,这就是子字符串移动位数计算式的由来。 如果我们提前将所有子字符串的部分匹配值计算出来,就可以知道匹配失败后的移动位数,所以在KMP算法中我们建立NEXT值表来存储这些值(next值就是部分匹配值加1)。 下面我们利用实例详细介绍求NEXT值表的算法: 子串(模式串):ababf ①:在字符a之前没有字符,所以默认为0 ②:在字符b之前只有字符a,无前缀和后缀,所以next值为1 ③:在字符a之前有字符ab,前缀为a,后缀为b,无公共子串,所以next值为1 ④:在字符b之前有字符aba,在步骤③中做了a和b的比较,所以不再需要比较,此时只需要比较新字符a和首字符a是否相同,在此时的实例中是相同的,所以next值为上一个字符的next值加1,所以现在的next值为2 ⑤:在字符f之前有字符abab,在步骤④已知有一个相同的字符,此时移位与新字符b比较,发现依然相等,所以next值为3 依次类推 计算NEXT值的函数C语言实现如下:部分匹配和部分匹配值
NEXT值表:
void NEXT(char s[],int next[])
{
int i,j;
i=1;
j=0;
next[1]=-1;
while(iKMP算法C语言实现代码如下:
希望本文对大家理解KMP算法有帮助,next函数的算法讲解的不够清晰,我会考虑再写一篇针对next函数的博文,大家可以依照实例逐步推导,可能有所帮助。
int Search_KMP(char m[],char n[],int next[])//消除在后续匹配失败后的回溯,已知next值表
{
int i,j,k;
for (i=1; i<=m[0]; i++)
{
j=1;//在找到相同字符之前,一直是子串的首字符与主串比较
if (m[i]==n[j])
{
for (k=i; k<=m[0],j<=n[0]; k++,j++)
{
if (m[k]!=n[j])
{
break;
}
}
if (j==n[0]+1)//两种出循环的状态,正常循环结束j指向子串末尾,非正常出循环j不会指向子串末尾
{
return i;
}
else
{
i=j-next[j]+1;
}
}
}
return 0;
}