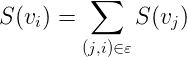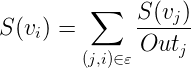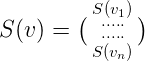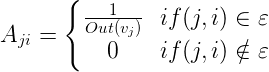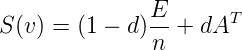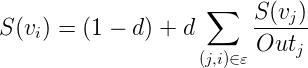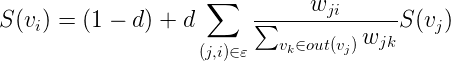【TextRank】关键词提取 算法原理 公式推导 源码分析

1.前言

    在介绍TextRank前，我想先给大家介绍下PageRank，实质上个人认为可以把TextRank当做PageRank2.0。

    谷歌的两位创始人的佩奇和布林，借鉴了学术界评判学术论文重要性的通用方法，“那就是看论文的引用次数”。由此想到网页的重要性也可以根据这种方法来评价。于是PageRank的核心思想就诞生了：

• 如果一个网页被很多其他网页链接到的话说明这个网页比较重要，也就是PageRank值会相对较高
• 如果一个PageRank值很高的网页链接到一个其他的网页，那么被链接到的网页的PageRank值会相应地因此而提高

 2.PageRank算法原理

      从PageRank的核心思想出发，我们

• 用定义这个页面的PageRank值
• 用来表示所有其他可以链接到这个页面的集合
• 那么便可以用来定义集合中的其中一个（由页面 链接到页面）

      我们可以给一个页面的PageRank值做这样的定义：

                                                      

    

以上图为例，PangRank的值就可以表示为：

                                                         

这样的计算有个很明显的漏洞，可以看到除了C点，其他三个点都外链了2个节点，那么对于B,D来说，是可以选择不去A的而去另外一个链接。所以外链进入A是有一定概率的。针对这点修整PangRank的表示方法：

                                                        

用矩阵的思想处理这个公式，设定：

• 为一个N维的PangRank值向量，
• 为所有页面的集合，且A有这样定义:
• 

那么对于大量PageRank，我们便可以转化为这样的形式：

                                                             

这样看似优化了很多，但是还存在一定的问题，我们得事先知道其他相关网站的PageRank值，才能得到指定网站的PageRank值。而其他网站的PageRank值还得从一些具有其链接的网站的PageRank值求得。这就变成了一个先有鸡还是先有蛋的问题。

PageRank采用power iteration来解决这个问题:

我们给定一个初始值假定为，然后通过下式子不断的迭代求解：

                                                             

 直到最后收敛于，即差别小于某个阈值。

于是计算PageRank值的过程就变成了一个 Markov 过程，那么PageRank算法的证明也就转为证明 Markov 过程的收敛性证明，

若一个 Markov 过程收敛，那么它的状态转移矩阵需要满足：

• stochastic matrix：则行至少存在一个非零值，即必须存在一个外链接（没有外链接的网页被称为dangling pages）；
• 不可约（irreducible）：即矩阵所对应的有向图必须是强连通的，对于任意两个节点，存在一个从到的路径；
• 非周期性（aperiodic）：即每个节点存在自回路。

显然，在一般情况下，这样的情况都是不满足的，为了满足性质stochastic matrix，可以把全为0的行替换为，其中为单位向量；同时为了满足性质不可约、非周期，需要做平滑处理：     

（个人觉得算法领域很多公式的可解释性不强，大多是为了解决某些限定条件，而人为选择的比较好的优化方式，比如下面公式，把的矩阵乘以的一个阻尼系数,(这个通常取0.85实践出来的，好像没什么数学解释)，实质上是为了给数据做一个平滑处理，都加上一个实质是为了替代为零项）

                                                                        

于是

                                                                        

就被改写为：

                                                                        

3.TextRank算法原理

     用TextRank提取来提取关键词，用PageRank的思想来解释它：

• 如果一个单词出现在很多单词后面的话，那么说明这个单词比较重要
• 一个TextRank值很高的单词后面跟着的一个单词，那么这个单词的TextRank值会相应地因此而提高

这样TextRank的公式就可以由PageRank公式改写为：

                                                      

公式的意思很明显：

     TextRank中一个单词的权重取决于与在前面的各个点组成的这条边的权重，以及这个点到其他其他边的权重之和。

 

4.python编程实现

   因为在了解textrank的时候，参考了jieba分词和TextRank4zh这2个开源库的写法。但是两者无论写法和运算规则都有很大出入，结合公式来说本人觉得jieba做的更符合公式，TextRank4zh更具有准确性，因为TextRank4zh在公式上面做了一定的优化。

Jieba分词TextRank：

• 对每个句子进行分词和词性标注处理
• 过滤掉除指定词性外的其他单词，过滤掉出现在停用词表的单词，过滤掉长度小于2的单词
• 将剩下的单词中循环选择一个单词，将其与其后面4个单词分别组合成4条边。

例如：         ['有','媒体', '曝光','高圆圆', '和', '赵又廷','现身', '台北', '桃园','机场','的', '照片']
        对于‘媒体‘这个单词，就有（'媒体', '曝光'）、（'媒体', '圆'）、（'媒体', '和'）、（'媒体', '赵又廷'）4条边，且每条边权值为1，当这条边在之后再次出现时，权值再在基础上加1.

• 有了这些数据后，我们就可以构建出候选关键词图，图的概念有基础的人可能会很好理解，不理解其实也没关系，按上面例子，你只用知道这一步我们把2个单词组成的边，和其权值记录了下来。
• 这样我们就可以套用TextRank的公式，迭代传播各节点的权值，直至收敛。
• 对结果中的Rank值进行倒序排序，筛选出前面的几个单词，就是我们需要的关键词了。

def textrank(self, sentence, topK=20, withWeight=False, allowPOS=('ns', 'n', 'vn', 'v'), withFlag=False):

    self.pos_filt = frozenset(allowPOS)
    # 定义无向有权图
    g = UndirectWeightedGraph()
    # 定义共现词典
    cm = defaultdict(int)
    # 分词
    words = tuple(self.tokenizer.cut(sentence))
    # 依次遍历每个词
    for i, wp in enumerate(words):
        # 词i 满足过滤条件
        if self.pairfilter(wp):
            # 依次遍历词i 之后窗口范围内的词
            for j in xrange(i + 1, i + self.span):
                # 词j 不能超出整个句子
                if j >= len(words):
                    break
                # 词j不满足过滤条件，则跳过
                if not self.pairfilter(words[j]):
                    continue
                # 将词i和词j作为key，出现的次数作为value，添加到共现词典中
                if allowPOS and withFlag:
                    cm[(wp, words[j])] += 1
                else:
                    cm[(wp.word, words[j].word)] += 1
    # 依次遍历共现词典的每个元素，将词i，词j作为一条边起始点和终止点，共现的次数作为边的权重
    for terms, w in cm.items():
        g.addEdge(terms[0], terms[1], w)
    
    # 运行textrank算法
    nodes_rank = g.rank()
    
    # 根据指标值进行排序
    if withWeight:
        tags = sorted(nodes_rank.items(), key=itemgetter(1), reverse=True)
    else:
        tags = sorted(nodes_rank, key=nodes_rank.__getitem__, reverse=True)

    # 输出topK个词作为关键词
    if topK:
        return tags[:topK]
    else:
        return tags

 关于有向图的数据结构：

def addEdge(self, start, end, weight):
    # use a tuple (start, end, weight) instead of a Edge object
    self.graph[start].append((start, end, weight))
    self.graph[end].append((end, start, weight))

关于TextRank的手写：

def rank(self):
    ws = defaultdict(float)
    outSum = defaultdict(float)

    wsdef = 1.0 / (len(self.graph) or 1.0)
    # 初始化各个结点的权值
    # 统计各个结点的出度的次数之和
    for n, out in self.graph.items():
        ws[n] = wsdef
        outSum[n] = sum((e[2] for e in out), 0.0)

    # this line for build stable iteration
    sorted_keys = sorted(self.graph.keys())
    # 遍历若干次
    for x in xrange(10):  # 10 iters
        # 遍历各个结点
        for n in sorted_keys:
            s = 0
            # 遍历结点的入度结点
            for e in self.graph[n]:
                # 将这些入度结点贡献后的权值相加
                # 贡献率 = 入度结点与结点n的共现次数 / 入度结点的所有出度的次数
                s += e[2] / outSum[e[1]] * ws[e[1]]
            # 更新结点n的权值
            ws[n] = (1 - self.d) + self.d * s

    (min_rank, max_rank) = (sys.float_info[0], sys.float_info[3])

    # 获取权值的最大值和最小值
    for w in itervalues(ws):
        if w < min_rank:
            min_rank = w
        if w > max_rank:
            max_rank = w

    # 对权值进行归一化
    for n, w in ws.items():
        # to unify the weights, don't *100.
        ws[n] = (w - min_rank / 10.0) / (max_rank - min_rank / 10.0)

    return ws

jieba.analyse.textrank完整源码如下：

#!/usr/bin/env python
# -*- coding: utf-8 -*-

from __future__ import absolute_import, unicode_literals
import sys
from operator import itemgetter
from collections import defaultdict
import jieba.posseg
from .tfidf import KeywordExtractor
from .._compat import *


class UndirectWeightedGraph:
    d = 0.85

    def __init__(self):
        self.graph = defaultdict(list)

    def addEdge(self, start, end, weight):
        # use a tuple (start, end, weight) instead of a Edge object
        self.graph[start].append((start, end, weight))
        self.graph[end].append((end, start, weight))

    def rank(self):
        ws = defaultdict(float)
        outSum = defaultdict(float)

        wsdef = 1.0 / (len(self.graph) or 1.0)
        for n, out in self.graph.items():
            ws[n] = wsdef
            outSum[n] = sum((e[2] for e in out), 0.0)

        # this line for build stable iteration
        sorted_keys = sorted(self.graph.keys())
        for x in xrange(10):  # 10 iters
            for n in sorted_keys:
                s = 0
                for e in self.graph[n]:
                    s += e[2] / outSum[e[1]] * ws[e[1]]
                ws[n] = (1 - self.d) + self.d * s

        (min_rank, max_rank) = (sys.float_info[0], sys.float_info[3])

        for w in itervalues(ws):
            if w < min_rank:
                min_rank = w
            if w > max_rank:
                max_rank = w

        for n, w in ws.items():
            # to unify the weights, don't *100.
            ws[n] = (w - min_rank / 10.0) / (max_rank - min_rank / 10.0)

        return ws


class TextRank(KeywordExtractor):

    def __init__(self):
        self.tokenizer = self.postokenizer = jieba.posseg.dt
        self.stop_words = self.STOP_WORDS.copy()
        self.pos_filt = frozenset(('ns', 'n', 'vn', 'v'))
        self.span = 5

    def pairfilter(self, wp):
        return (wp.flag in self.pos_filt and len(wp.word.strip()) >= 2
                and wp.word.lower() not in self.stop_words)

    def textrank(self, sentence, topK=20, withWeight=False, allowPOS=('ns', 'n', 'vn', 'v'), withFlag=False):
        """
        Extract keywords from sentence using TextRank algorithm.
        Parameter:
            - topK: return how many top keywords. `None` for all possible words.
            - withWeight: if True, return a list of (word, weight);
                          if False, return a list of words.
            - allowPOS: the allowed POS list eg. ['ns', 'n', 'vn', 'v'].
                        if the POS of w is not in this list, it will be filtered.
            - withFlag: if True, return a list of pair(word, weight) like posseg.cut
                        if False, return a list of words
        """
        self.pos_filt = frozenset(allowPOS)
        g = UndirectWeightedGraph()
        cm = defaultdict(int)
        words = tuple(self.tokenizer.cut(sentence))
        for i, wp in enumerate(words):
            if self.pairfilter(wp):
                for j in xrange(i + 1, i + self.span):
                    if j >= len(words):
                        break
                    if not self.pairfilter(words[j]):
                        continue
                    if allowPOS and withFlag:
                        cm[(wp, words[j])] += 1
                    else:
                        cm[(wp.word, words[j].word)] += 1

        for terms, w in cm.items():
            g.addEdge(terms[0], terms[1], w)
        nodes_rank = g.rank()
        if withWeight:
            tags = sorted(nodes_rank.items(), key=itemgetter(1), reverse=True)
        else:
            tags = sorted(nodes_rank, key=nodes_rank.__getitem__, reverse=True)

        if topK:
            return tags[:topK]
        else:
            return tags

    extract_tags = textrank

 

打赏一下作者：