动态规划经典例题汇总

动态规划经典例题汇总

0-1背包问题

[动态规划，回溯有何区别] https://www.cnblogs.com/genialx/p/10191366.html
[什么是动态规划，动态规划的意义？]https://www.zhihu.com/question/23995189

选或不选这类问题：
例1：给定一组数据，相邻两个数不能同时选择，求如何选择使得所选数之和最大？
$arr=[1,2,4,1,7,8,3]$ 直接看最后一个数，它有两种方案，选或不选。
$dp[6]=max(dp[4]+arr[6],dp[5])$
递推公式： $dp[i]=max(dp[i-2]+arr[i],dp[i-1])$
递推出口： $dp[0]=arr[0]，dp[1]=max(arr[0],arr[1])$

例2：给定一数组，和一个目标数tar，问有没有几个数相加之和等于tar?
$arr=[3,34,4,12,5,2]$ 每个数有两种方案，选或者不选
$subset(arr,i,s)=subset(arr,i-1,s)||subset(arr,i-1,s-arr[i])$
其中s为目标数，当i=5时，s=tar 。 看递推公式||左侧，为不选该数的情况，右侧为选择该数的情况，若选择了，则目标数发生变化
递推出口： if $s==0$: return $true$
                   if $i==0$: return $arr[0]==s$
                  if $arr[i]>s$: return $subset(arr,i-1,s)$ 即只有不选这种情况
非递归需要用二维数组来保存，此题类似0-1背包问题

int backpack(vector<int>&w, vector<int>&v, int capacity){
	vector<int>temp(capacity + 1, 0);
	vector<vector<int>>dp(w.size(), temp);

	for (int j = 0; j < capacity; ++j){   //初始化第一行
		if (j >= w[0])
		{
			dp[0][j] = v[0];
		}
	}
	for (int i = 1; i < w.size(); ++i){
		for (int j = 1; j <= capacity; ++j){
			if (j < w[i])//包装不进了
			{
				dp[i][j] = dp[i - 1][j];
			}
			else{
				dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - w[i]] + v[i]);
			}
		}
	}
	return dp[w.size() - 1][capacity - 1];
}

空间优化

• 上述二维数组相当于从上向下填表，可以看到填下一行时只需用到上一行的信息，因此可用一维数组来优化.
• 此时dp[j]等于第i次循环结束后dp[i][j]的值，即前i个物体在容量为j时的最大价值。
• dp[i][j] 由 dp[i-1][j] 和 dp[i-1][j-w[i]] 两个状态得到。 在第i次循环之前， dp[i]就是dp[i-1][j] ，那怎么得到dp[i-1][j-w[i]]？
• 内层从右往左循环，就可保证dp[j-w[i]]存储的是dp[i-1][j-w[i]]。如果正序的话，会用更新后的dp[j-w[i]]来计算此时的dp[j]

int backpack_better(vector<int>&w, vector<int>&v, int capacity){
	vector<int>dp(capacity + 1);
	for (int i = 0; i < w.size(); i++)    //里面的循环包含了初始化第一行的步骤
	{
		for (int j = capacity; j >= 0; j--)
		{
			if (j - w[i] >= 0)
				dp[j] = max(dp[j - w[i]] + v[i], dp[j]);
		}
	}
	return dp[capacity];
}

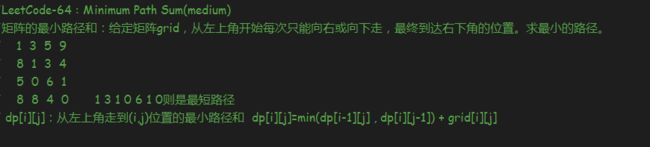
矩阵的最小路径和

int minPathSum(vector<vector<int>>& grid) {
	int row = grid.size(), col = grid[0].size();
	if (row == 0 || col == 0) return -1;
	vector<int>temp(col, 0);
	vector<vector<int>>dp(row, temp);
	dp[0][0] = grid[0][0];
	for (int j = 1; j < col; ++j)  //初始化第一行
		dp[0][j] = dp[0][j - 1] + grid[0][j];
	for (int i = 1; i < row; ++i)  //初始化第一列
		dp[i][0] += dp[i - 1][0] + grid[i][0];

	for (int i = 1; i < row; ++i)
	for (int j = 1; j < col; ++j){
		dp[i][j] = min(dp[i - 1][j], dp[i][j - 1]) + grid[i][j];
	}
	return dp[row - 1][col - 1];
}

从递推公式可以看出，当前行只会依赖于上方和左侧的值，只开一个一维数组也可解决。问题是开多大？
所以要么开辟row大小的数组从左向右滚，要么开col大小的数组从上向下滚。row跟col哪个小用哪个的值开辟数组会省空间

int minPathSum_better(vector<vector<int>>& grid) {
	int row = grid.size(), col = grid[0].size();
	if (row == 0 || col == 0) return -1;
	int more = max(row, col);
	int less = min(row, col);
	bool flag = row > col;  //flag为true，从上向下滚
	vector<int>dp(less, 0);
	dp[0] = grid[0][0];
	for (int i = 1; i < less; ++i)
		dp[i] = dp[i - 1] + (flag ? grid[0][i] : grid[i][0]);
	for (int j = 1; j < more; ++j)
	{
		dp[0] += flag ? grid[j][0] : grid[0][j];
		for (int i = 1; i < less; ++i)
			dp[i] = min(dp[i], dp[i - 1]) + (flag ? grid[j][i] : grid[i][j]);
	}
	return dp[less - 1];
}

硬币找零

int coinChange(vector<int>& coins, int amount)
{
	if (coins.size() == 0 || amount <= 0)   return 0;
	vector<int>temp(amount + 1, 0);
	vector<vector<int>>dp(coins.size(), temp);
	for (int j = 1; j <= amount; ++j){
		if (j%coins[0] == 0)
		{
			dp[0][j] = j / coins[0];  //初始化第一行，注意该dp矩阵建立大小跟01背包一样
		}
		else dp[0][j] = INT_MAX;
	}
	for (int i = 1; i < coins.size(); ++i)
	for (int j = 1; j <= amount; ++j)
	{
		int help = INT_MAX;
		for (int k = 0; j - coins[i] * k >= 0; ++k)
		{
			if (dp[i - 1][j - k*coins[i]] != INT_MAX)
			{
				help = min(help, dp[i - 1][j - k*coins[i]] + k);
			}
		}
		dp[i][j] = help;
	}
	return dp[coins.size() - 1][amount] == INT_MAX ? -1 : dp[coins.size() - 1][amount];
}

注意到，以例1为例，dp[1][6]用到上排的元素有：dp[0][6],dp[0][4],dp[0][2],dp[0][0] 考虑到在计算dp[1][4]时已经用到了dp[0][4],dp[0][2],dp[0][0]
递推公式可改为： dp[i][j]=min( dp[i-1][j], dp[i][j-coins[i]]+1)

int coinChange_better(vector<int>& coins, int amount)
{
	if (coins.size() == 0 || amount <= 0)   return 0;
	vector<int>temp(amount + 1, 0);
	vector<vector<int>>dp(coins.size(), temp);
	for (int j = 1; j <= amount; ++j){
		if (j%coins[0] == 0)
		{
			dp[0][j] = j / coins[0];
		}
		else dp[0][j] = INT_MAX;
	}
	for (int i = 1; i < coins.size(); ++i)
	for (int j = 1; j <= amount; ++j)
	{
		/*******************改动*********************/
		int help = INT_MAX;
		if (j - coins[i] >= 0 && dp[i][j - coins[i]] != INT_MAX)
			help = dp[i][j - coins[i]] + 1;
		dp[i][j] = min(help, dp[i - 1][j]);
		/*******************************************/
	}
	return dp[coins.size() - 1][amount] == INT_MAX ? -1 : dp[coins.size() - 1][amount];
}

从coinChange_better可以看出，只用到了本行元素和正上方元素， 类似LeetCode-64 : Minimum Path Sum ，使用一维数组进行优化

int coinChange_best(vector<int>& coins, int amount)
{
	if (coins.size() == 0 || amount < 0) {
		return 0;
	}
	vector<int>dp(amount + 1, INT_MAX);
	dp[0] = 0;
	for (int j = 1; j <= amount; ++j){
		if (j%coins[0] == 0)
		{
			dp[j] = j / coins[0];
		}
	}
	for (int i = 0; i < coins.size(); ++i)
	for (int j = 0; j <= amount; ++j)
	{
		int help = INT_MAX;
		if (j - coins[i] >= 0 && dp[j - coins[i]] != INT_MAX)
			help = dp[j - coins[i]] + 1;
		dp[j] = min(help, dp[j]);
	}
	return dp[amount] == INT_MAX ? -1 : dp[amount];
}

最长递增子序列

给定未排序的整数数组，找到最长的递增子序列的长度。
Input:[10, 9, 2, 5, 3, 7, 101, 18] Output : 4 Explanation : The longest increasing subsequence is[2, 3, 7, 101], therefore the length is 4.
dp[i]：遍历到第i个数时的最长递增子序列长度 $dp[i]=max(1,(dp[i-k]+1)|nums[i]>nums[i-k])$

int lengthOfLIS(vector<int>& nums) {
	if (nums.empty()) return 0;
	vector<int>dp(nums.size(), 1);
	for (int i = 1; i < nums.size(); ++i)
	for (int j = i - 1; j >= 0; --j)
	{
		if (nums[i]>nums[j])
			dp[i] = max(dp[i], dp[j] + 1);
	}
	//	return dp[nums.size()-1];  这里不正确，例如nums = {1,3,6,7,9,4,10,5,6};  dp[nums.size()-1]=5;  应返回dp数组中最大那个值
	int res = 0;
	for (auto c : dp){
		res = max(res, c);
	}
	return res;
}

如果我们另开一个数组，记录连续的子序列中的最大值，如长度为1的递增子序列最大值为 MaxV[1] ，长度为2的递增子序列最大值为MaxV[2]
这样只需比较当前数nums[i]与MaxV[nMaxLIS]，MaxV[nMaxLIS-1]…只要大于其中一个，则找到当前数应该加入的位置

int lengthOfLIS_better(vector<int>& nums) {
	if (nums.empty()) return 0;
	vector<int>dp(nums.size(), 1);
	vector<int>MaxV(nums.size() + 1, -1);
	MaxV[1] = nums[0];
	MaxV[0] = INT_MIN;   //这项是为了更新长度为1的子序列
	//如序列为10 2 3，进入内层for循环后小于当前MaxV[1]=10，如果到此就break肯定是不对的，我们要替换MaxV[1]为2 
	int nMaxLIS = 1;  //当前数组最长递增子序列的长度

	for (int i = 1; i < nums.size(); ++i)
	{
		int j;
		for (j = nMaxLIS; j >= 0; --j){
			if (nums[i]>MaxV[j])
			{
				dp[i] = j + 1;  break;
			}
		}
		//更新信息  
		if (dp[i] > nMaxLIS)
		{
			nMaxLIS = dp[i];     MaxV[nMaxLIS] = nums[i];
		}
		else if (MaxV[j] < nums[i] && nums[i] < MaxV[j + 1])
		{
			MaxV[j + 1] = nums[i];  //例如  1 2 3 4  和 1 2 3 5都是长度为4的递增序列，但我们肯定选择1 2 3 4因为这样有助长度的增长
		}
	}
	return nMaxLIS;
}

上述时间复杂度依然为O(N^2)，利用二分查找优化dp数组生成过程，将时间复杂度降为O(NlogN)

• dp[i]代表以i为结尾的最长递增序列的长度，ends数组则是存放递增的序列的具体值，right为ends数组的分割点，right左侧为有效区
• nums=[2,1,5,3,6,4] 初始：dp[0]=1，right=0，ends[0]=2 有效区为[0,0]
• 遍历至nums[1]=1 : 在有效区找到最左边大于等于nums[1]的数，发现是nums[right]=2，则将该位置替换成nums[1] 此时，ends=[1]，有效区为[0,0]
• 遍历至nums[2]=5 : 有效区没有比5大的，则将5加入ends，right右移 dp[2]=2
• 遍历至nums[3]=3 :有效区最左侧大于3的是5，替换 dp[3]=2 ends=[1,3]
• 遍历至nums[4]=6: 有效区无大于6的，ends=[1,3,6] right=2
• 遍历至nums[5]=4 :替换掉6 ends=[1,3,4]
• 在有效区中可用二分查找找到最左侧大于当前数的数
• ends数组并不是最终的最长递增序列的元素，如[1,5,3,4,2] 最后ends=[1,2,4]

int lengthOfLIS_best(vector<int>& nums) {
   if (nums.empty()) return 0;
   vector<int>dp(nums.size(), 1);
   vector<int>ends(nums.size(), 0);
   int right = 0;
   ends[0] = nums[0];
   int l = 0, r = 0, m = 0;
   for (int i = 1; i < nums.size();++i)
   {
   	l = 0; r = right;
   	while (l<=r)
   	{
   		m = l + (r - l) / 2; 
   		if (nums[i]>ends[m])
   			l = m + 1;
   		else r = m - 1;
   	}
   	right = max(right, l);
   	ends[l] = nums[i];
   	dp[i] = l + 1;
   }

   int res = 0;
   for (auto c : dp){
   	res = max(res, c);
   }
   return res;
}

最长公共子序列

string LCSE(string str1, string str2){
	if (str1.empty() || str2.empty())  return "";
	vector<vector<int> > dp(str1.size(), vector<int>(str2.size(), 0));
	dp[0][0] = (str1[0] == str2[0]) ? 1 : 0;
	for (int i=1; i < str1.size();++i)
	{
		dp[i][0] = max(dp[i - 1][0], (str1[i]==str2[0])?1:0);  //初始化第一列
	}
	for (int j = 1; j < str2.size();++j)
	{
		dp[0][j] = max(dp[0][j - 1], (str1[0]==str2[j]  ) ? 1 : 0);  //初始化第一行
	}
	for (int i = 1; i < str1.size();++i)
	for (int j = 1; j < str2.size();++j)
	{
		dp[i][j] = max(dp[i - 1][j], dp[i][j - 1]);
		if (str1[i] == str2[j]) 
			dp[i][j] = max(dp[i][j], dp[i - 1][j - 1] + 1);
	}
	//dp数组右下角的点就是最长公共子序列的长度，如果只需要知道长度，可用一维数组来优化
	//但是我们要得到这个子序列，就需要从右下角开始移动至左上角 ,判断这个dp是怎么来的
	string res ="";
	int m = str1.size() - 1, n = str2.size() - 1;
	int index = dp[m][n] - 1;
	while (index>=0)
	{
		if (n > 0 && dp[m][n] == dp[m][n - 1])  //如果dp[i][j]==dp[i-1][j]，说明dp[i - 1][j - 1] + 1不是必须的选择，向上移动
			--n;
		else if (m > 0 && dp[m][n] == dp[m - 1][n])
			--m;
		else{
			res= str1[m]+res;   //如果dp[i][j]>dp[i-1][j] 且dp[i][j]>dp[i][j-1]，说明在计算dp[i][j]一定是选择了dp[i - 1][j - 1] + 1，此时str1[i]==str2[j]
			--index;
			--m;
			--n;
		}
	}
	return res;
}