浮点数表示
-
- 浮点数表示
- 浮点数的规格化表示
- 浮点数的表示范围
- 浮点数的表示精度
- 参考资料
之前的一些工作当中碰到了很多有关浮点数的问题,比如浮点数的表达范围、表达精度、浮点数的存储方式、浮点数的强制类型转换等等,因此感觉有必要系统了解一下有关浮点数的问题。
—————————— 浮点数表示 ——————————
浮点数是一种 公式化 的表达方式,用来近似表示实数,并且可以在表达范围和表示精度之间进行权衡(因此被称为浮点数)。
浮点数通常被表示为:
\(N = M\times R^E\)
比如: \(12.345 = 1.2345\times 10^1\)
其中,M(Mantissa)被称为浮点数的 尾数 ,R(Radix)被称为阶码的 基数 ,E(Exponent)被称为阶的 阶码 。计算机中一般规定R为2、8或16,是一个确定的常数,不需要在浮点数中明确表示出来。
因此,在已知标准下,要表示浮点数,
一是要给出尾数M的值,通常用定点小数形式表示,它决定了浮点数的表示精度,即可以给出的有效数字的位数。
二是要给出阶码,通常用定点整数形式表示,它指出的是小数点在数据中的位置,决定了浮点数的表示范围。因此,在计算机中,浮点数通常被表示成如下格式:(假定为32位浮点数,基为2,其中最高位为符号位)
—————————— 浮点数的规格化表示 ——————————
按照上面的指数表示方法,一个浮点数会有不同的表示:
\(0.3\times10^0\);\(0.03\times10^1\);\(0.003\times10^2\);\(0.0003\times10^3\);
为了提高数据的表示精度同时保证数据表示的唯一性,需要对浮点数做规格化处理。
在计算机内,对非0值的浮点数,要求尾数的绝对值必须大于基数的倒数,即\(|M|\ge \frac{1}{R}\)。
即要求尾数域的最高有效位应为1,称满足这种表示要求的浮点数为规格化表示:把不满足这一表示要求的尾数,变成满足这一要求的尾数的操作过程,叫作浮点数的规格化处理,通过尾数移位和修改阶码实现。
比如,二进制原码的规格化数的表现形式:(0正1负)
正数 0.1xxxxxx
负数 1.1xxxxxx
注意,尾数的最高位始终是1,因此我们完全可以省略掉该位。
至此,我们引入IEEE754 标准,该标准约束了浮点数的大部分使用设置:(尾数用原码;阶码用“移码”;基为2)
(1) 尾数用原码,且隐藏尾数最高位。
原码非0值浮点数的尾数数值最高位必定为 1,因此可以忽略掉该位,这样用同样多的位数就能多存一位二进制数,有利于提高数据表示精度,称这种处理方案使用了隐藏位技术。当然,在取回这样的浮点数到运算器执行运算时,必须先恢复该隐藏位。
(2) 阶码使用“移码”,基固定为2
如下图的32bit浮点数和64bit浮点数,从最高位依次是符号位、阶码和尾数
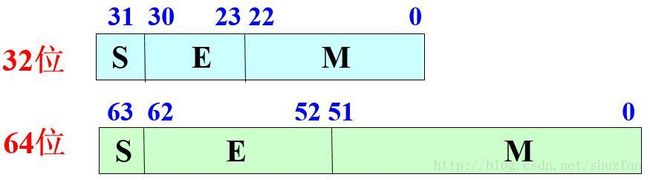
于是,
一个规格化的32位浮点数x的真值为:
\(x = (-1)^s\times(1.M)\times2^{E-127}\)
一个规格化的64位浮点数x的真值为:
\(x = (-1)^s\times(1.M)\times2^{E-1023}\)
下面举一个32位单精度浮点数-3.75表示的例子帮助理解:
(1) 首先转化为2进制表示
\(-3.75 = -(2+1+1/2+1/4) = -1.111\times2^1\)
(2) 整理符号位并进行规格化表示
\(-1.111\times2^1 = (-1)^{(1)}\times(1+0.1110\ 0000\ 0000\ 0000\ 0000\ 000)\times2^1\)
(3) 进行阶码的移码处理
\((-1)^{(1)}\times(1+0.1110\ 0000\ 0000\ 0000\ 0000\ 000)\times2^1\)
\(=(-1)^{(1)}\times(1+0.1110\ 0000\ 0000\ 0000\ 0000\ 000)\times2^{128-127}\)
于是,符号位S=1,尾数M为\(1110\ 0000\ 0000\ 0000\ 0000\ 000\)阶码E为\(128_{10}=1000\ 0000_2\),则最终的32位单精度浮点数为
\(1\ 1110\ 0000\ 0000\ 0000\ 0000\ 000\ 1000\ 0000\)
—————————— 浮点数的表示范围 ——————————
通过上面的规格化表示,我们可以很容易确定浮点数的表示范围:
既然有表示范围,那肯定也有不能表示的数值:
首先来说明溢出值,如下图:
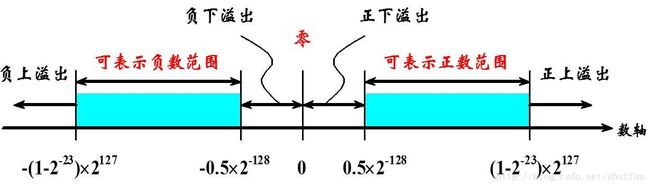
(1)无穷值:
如果指数\(E=11111111_2=255_{10}\)且尾数\(M=0\),则根据符号位S分别表示\(+\infty\)和\(-\infty\)。因此,一个有效的32位浮点数其指数最大只能为254。
此外,无穷具有传递性,比如
(+∞) + (+7) = (+∞)
(+∞) × (−2) = (−∞)
(+∞) × 0 = NaN
(2)零值:
如果指数\(E=0\)且尾数\(M=0\)时,表示机器0.需要注意的是,这里的0也是有符号的,在数值比较的时候 \(+0=-0\); 但在一些特殊操作下,二者并不显相等,比如\(\log(x)\), \(\frac{1}{+0} \neq \frac{1}{-0}\)。
此外,处于负下溢出和负上溢出之间的数值会被直接归为0。
(3)NAN:
如果\(E=0\)且尾数\(M\neq 0\),则表示这个值不是一个真正的值(Not A Number)。NAN又分成两类:QNAN(Quiet NAN)和SNAN(Singaling NAN)。QNAN与SNAN的不同之处在于,QNAN的尾数部分最高位定义为1,SNAN最高位定义为0;QNAN一般表示未定义的算术运算结果,如\(\frac{0}{0}\), \(\infty \times 0\), \(sqrt(-1)\);SNAN一般被用于标记未初始化的值,以此来捕获异常。
—————————— 浮点数的表示精度 ——————
一般提到浮点数的精度(有效位数)的时候,总是会出现 float的有效位为6~7位, double的有效位为15~16位 。
下面以float为例,解释一下有效位数是怎样来的。
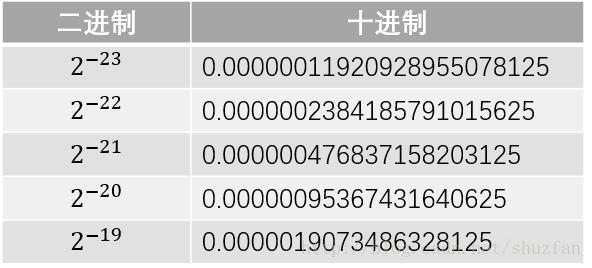
有效位数只和规格化浮点数的尾数部分有关,而尾数部分的位数是23位,因此我们首先列出下表
由上面的表格可以看出:
\(2^{-23}\) 和 \(2^{-22}\) 之间是存在间隔的,即0.0000001和0.0000002之间的小数我们是没有办法描述的,因此23位尾数最多只能描述到小数点后第7位;此外,我们通过四舍五入可以很容易发现\(0.0000003 = 0.0000004 = 2^{-23}+2^{-22}\), 这表明第7位有效数字只是部分准确。而第6位及之前的都是可以准确描述的,因此我们说float的有效位为6~7位。
—————————— 参考资料 ——————————
(1) WIKI 词条 “Floating Point”: https://en.wikipedia.org/wiki/Floating_point
(2) WIKI 词条 “IEEE floating point”: https://en.wikipedia.org/wiki/IEEE_floating_point
(2) 浮点异常值:NAN,QNAN,SNAN:
http://www.cnblogs.com/konlil/archive/2011/07/06/2099646.html