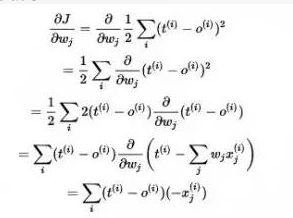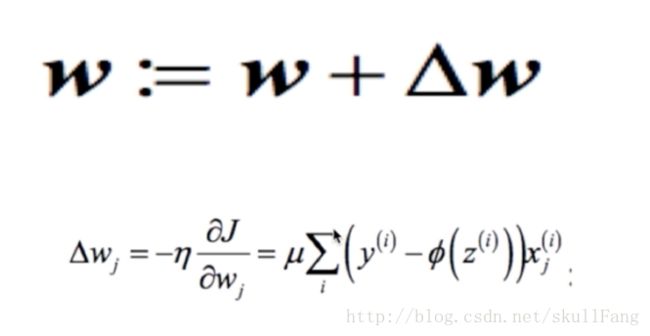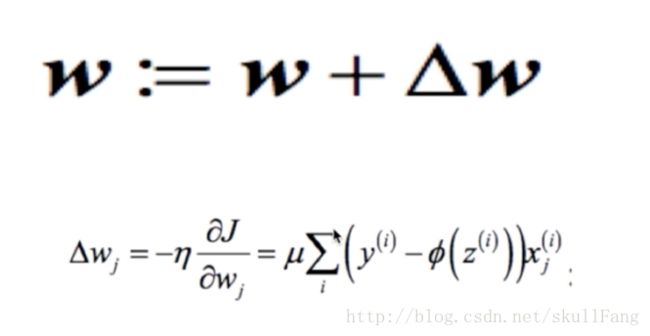神经网络-自适应神经元

自适应神经元

前言

本博客讲解的是自适应性神经元，为以后的深度学习打下基础。
本文章是阅览技术文档加以实现和理解。
原文地址：http://www.ranling.com/category/it/689240.html
这篇博客是继上一篇博客写下的。
神经网络-感知器：http://blog.csdn.net/skullfang/article/details/78564490#

感知机存在的问题

根据上一篇博客的算法来看 收敛就是感知机存在的最大问题。
如果有一个两个数据每一次迭代都不能达到正确，那么算法就会不停的更新权重，就是“学不停”！
另外一个缺陷就是学习效果有一定局限性，什么意思呢？就是一旦分类正确他就会停止更新权重，这会导致它只正对样本数据有正确结果，对其他的样本有很大的误差。

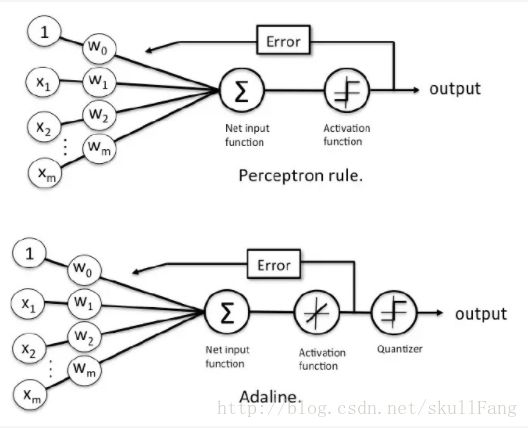
自适应神经元

前面的原理还是一样的，由“树突“刺激超过阈值就能激活。

这里使用的激活函数是一个线性激活函数，不再是单元阶跃函数。这个 函数最大的好处就是能够可微，既然可微就可以找到最小代价函数。这里定义一个和方差公式

注意这里后面那个小尾巴output(i)只是一个定义域，不要认为它是公式的一部分。

使用梯度下降算法，来找过系统的局部最优

既然梯度下降，我们的权重更新就是按照j(w)进行下降。
（△是大写希腊字母Delta表示变量的分量，▽读Nabla,奈不拉,也可以读作“Del”求偏导）

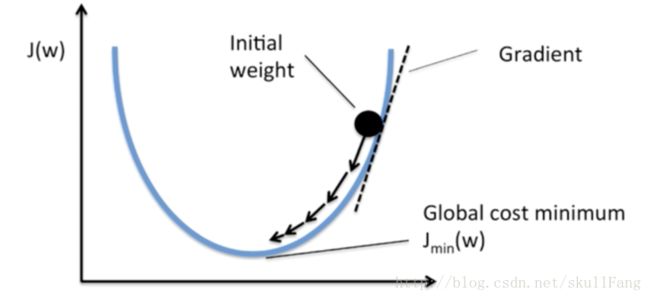
这里会有疑问为什么W的增量要加上损失函数的偏导数，我们仔细观察上面的梯度下降的图，w如果想要按照理想的方向走，那么损失函数的偏导是正数就说明w在jmin(w)右边，我们只需要用w减去那个偏导即可。同理如果ww在jmin(w)左边，偏导就是负数，我们只需要减去它，w就在往右边跑。

求偏导

整合一下

算法步骤

这个算法步骤跟上一篇博客感知器的步骤基本相同，不同的就是更新权重和更新阈值这里。感知器更新就是反复左右推，而这里使用了梯度下降的算法，理论上可以达到局部最优。
1、权重初始化
2、计算预测值
3、更新权重
4、更新阈值

权重初始化

与感知机一样把权重初始化为0或者比较小的随机数。

计算预测值

z=dot(W,X) W为权重向量，X为输入向量。
与感知器不同的是这里不需要转换为标签值。只需要一个z这个实数就可以。

更新权重

如上一章所示，W的增量是根据损失函数的偏导数。进行调整。

更新阈值

这里的阈值还是作为W向量的第0号元素（不明白怎么来的可以参考感知机那篇博文）那么更新方法也是一样的。只不过w0 没有Xj对应那么。
W（0）等于上图的公式不要后面Xj（i）那个尾巴。

代码部分

可以参考感知器的代码看，不一样的就是阈值和权重更新方面。看不懂的可以私信。

# -*- coding: utf-8 -*-
# @Time    : 2017/11/17 上午10:10
# @Author  : SkullFang
# @Email   : [email protected]
# @File    : main.py
# @Software: PyCharm
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from matplotlib.colors import ListedColormap
class AdalineGD(object):
    """
    eta : 学习率
    n_iter: 学习次数
    w_: 权重向量
    error_:错误判断次数
    """
    def __init__(self,eta=0.01,n_iter=50):
        """
        :param eta: 学习率
        :param n_iter: 次数
        """
        self.eta=eta
        self.n_iter=n_iter

    def fit(self,x,y):
        """
        :param x: 二维数组[向量，条数]
        :param y: 每一条的正确分类
        :return: 
        """
        self.w_=np.zeros(1+x.shape[1])
        self.cost_=[]

        for i in range(self.n_iter):
            output=self.net_input(x)
            error=(y-output)#对应公式
            self.w_[1:]+=self.eta * x.T.dot(error)
            self.w_[0]+=self.eta*error.sum()
            #损失函数 就是图中的J（W）
            cost=(error ** 2).sum()/2.0
            self.cost_.append(cost)

        return self



    def net_input(self,x):
        """
        这个是为了输入向量和权重向量做一下点积
        :param x: 输入向量
        :return: 
        """
        return np.dot(x,self.w_[1:]+self.w_[0])
        pass

    def predict(self, x):
        """
        算出分类结果
        :param x: 
        :return: 
        """
        return np.where(self.activation(x) >= 0.0, 1, -1)

    def activation(self,x):
        """
        激活函数
        :param x: 
        :return: 
        """
        return self.net_input(x)

函数调用部分

if __name__ == '__main__':
    file = "data/irisdata.csv"
    df=pd.read_csv(file,header=None)
    #前10行
    # print(df.head(10))
    #加载0到100行第4列
    y=df.loc[0:100,4].values
    y=np.where(y=='Iris-setosa',-1,1)
    #x要第0列和2列
    x=df.loc[0:100,[0,2]].values

    plt.scatter(x[:50, 0], x[:50, 1], color='red', marker='o', label='setosa')
    plt.scatter(x[50:100, 0], x[50:100, 1], color='blue', marker='x', label='versicolor')
    plt.legend(loc='upper left')



    ada=AdalineGD(eta=0.0001,n_iter=100)
    ada.fit(x,y)
    plot_decision_regions(x,y,classifier=ada,resolution=0.2)

画图函数

def plot_decision_regions(x,y,classifier,resolution=0.02):
    """
    用于结果展示
    :param x: 
    :param y: 
    :param classifier: 
    :param resolution: 
    :return: 
    """
    makers=('s','x','o','v')
    colors=('red','blue','lightgreen','gray','cyan')
    cmap=ListedColormap(colors[:len(np.unique(y))])

    x1_min,x1_max=x[:,0].min()-1,x[:,0].max()
    x2_min,x2_max=x[:,1].min()-1,x[:,1].max()

    print(x1_min,x1_max)
    print(x2_min,x2_max)

    xx1,xx2=np.meshgrid(np.arange(x1_min,x1_max,resolution),np.arange(x2_min,x2_max,resolution))

    #预测结果
    z=classifier.predict(np.array([xx1.ravel(), xx2.ravel()]).T)

    #画分界线
    z=z.reshape(xx1.shape)
    plt.contourf(xx1, xx2, z, alpha=0.4, cmap=cmap)
    plt.xlim(x1_min, x1_max)
    plt.ylim(xx2.min(), xx2.max())
    for idx, cl in enumerate(np.unique(y)):
        plt.scatter(x=x[y==cl,0],y=x[y==cl,1],alpha=0.0,c=cmap(idx),marker=makers[idx],label=cl)


    plt.show()

数据来源于比较经典的莺尾花数据。
数据地址为：
https://archive.ics.uci.edu/ml/machine-learning-databases/iris/iris.data
打开复制在本地创建csv数据即可。
大家可以自己跑一下看看效果。这里就不贴效果图了。有什么不明白的地方欢迎留言。