Siamese Network理解(附代码)
author:DivinerShi
文章地址:http://blog.csdn.net/sxf1061926959/article/details/54836696
提起siamese network一般都会引用这两篇文章:
《Learning a similarity metric discriminatively, with application to face verification》和《 Hamming Distance Metric Learning》。
本文主要通过论文《Learning a Similarity Metric Discriminatively, with Application to Face Verification》来理解siamese网络。
介绍
Siamese网络是一种相似性度量方法,当类别数多,但每个类别的样本数量少的情况下可用于类别的识别、分类等。传统的用于区分的分类方法是需要确切的知道每个样本属于哪个类,需要针对每个样本有确切的标签。而且相对来说标签的数量是不会太多的。当类别数量过多,每个类别的样本数量又相对较少的情况下,这些方法就不那么适用了。其实也很好理解,对于整个数据集来说,我们的数据量是有的,但是对于每个类别来说,可以只有几个样本,那么用分类算法去做的话,由于每个类别的样本太少,我们根本训练不出什么好的结果,所以只能去找个新的方法来对这种数据集进行训练,从而提出了siamese网络。siamese网络从数据中去学习一个相似性度量,用这个学习出来的度量去比较和匹配新的未知类别的样本。这个方法能被应用于那些类别数多或者整个训练样本无法用于之前方法训练的分类问题。
主要思想
主要思想是通过一个函数将输入映射到目标空间,在目标空间使用简单的距离(欧式距离等)进行对比相似度。在训练阶段去最小化来自相同类别的一对样本的损失函数值,最大化来自不同类别的一堆样本的损失函数值。给定一组映射函数![]() ,其中参数为W,我们的目的就是去找一组参数W。使得当
,其中参数为W,我们的目的就是去找一组参数W。使得当![]() 和
和![]() 属于同一个类别的时候,相似性度量
属于同一个类别的时候,相似性度量![]() 是一个较小的值,当
是一个较小的值,当![]() 和
和![]() 属于不同的类别的时候,相似性度量
属于不同的类别的时候,相似性度量![]() 较大。这个系统是用训练集中的成对样本进行训练。当
较大。这个系统是用训练集中的成对样本进行训练。当![]() 和
和![]() 来自相同类别的时候,最小化损失函数
来自相同类别的时候,最小化损失函数![]() ,当
,当![]() 和
和![]() 来自不同类别的时候,最大化
来自不同类别的时候,最大化![]() 。这里的
。这里的![]() 除了需要可微外不需要任何的前提假设,因为针对成对样本输入,这里两个相同的函数G,拥有一份相同的参数W,即这个结构是对称的,我们将它叫做siamese architecture。
除了需要可微外不需要任何的前提假设,因为针对成对样本输入,这里两个相同的函数G,拥有一份相同的参数W,即这个结构是对称的,我们将它叫做siamese architecture。
在这篇论文中,作者用这个网络去做面部识别,比较两幅图片是不是同一个人,而且这个网络的一个优势是可以去区分那些新的没有经过训练的类别的样本。
Siamese也算是降维方法的一种。常见的降维方法有PCA、LDA、Kernel-PCA、MDS、LLE、LB、ISOmap、FA等不做具体介绍。
网络结构
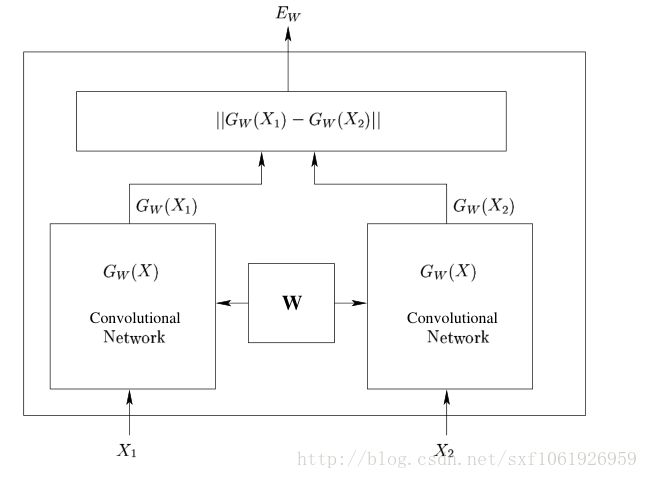
上图是论文中的网络结构图,左右两边两个网络是完全相同的网络结构,它们共享相同的权值W,输入数据为一对图片(X1,X2,Y),其中Y=0表示X1和X2属于同一个人的脸,Y=1则表示不为同一个人。即相同对为(X1,X2,0),欺骗对为(X1,X2’,1)针对两个不同的输入X1和X2,分别输出低维空间结果为 和
和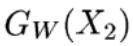 ,它们是由
,它们是由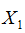 和
和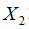 经过网络映射得到的。然后将得到的这两个输出结果使用能量函数
经过网络映射得到的。然后将得到的这两个输出结果使用能量函数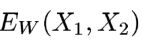 进行比较。
进行比较。
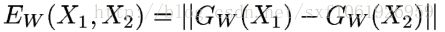
损失函数定义
我们假设损失函数只和输入和参数有关,那么我们损失函数的形式为:
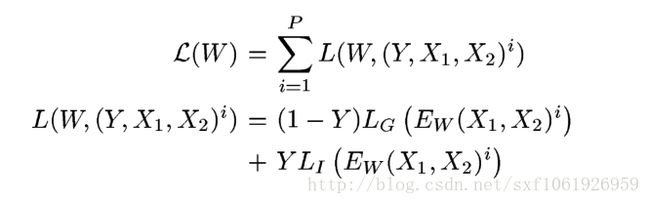
其中 是第i个样本,是由一对图片和一个标签组成的,其中LG是只计算相同类别对图片的损失函数,LI是只计算不相同类别对图片的损失函数。P是训练的样本数。通过这样分开设计,可以达到当我们要最小化损失函数的时候,可以减少相同类别对的能量,增加不相同对的能量。很简单直观的方法是实现这个的话,我们只要将LG设计成单调增加,让LI单调递减就可以了,但是我们要保证一个前提就是,不相同的图片对(image pairs)距离肯定要比相同图片对的距离大,那么就是要满足:
是第i个样本,是由一对图片和一个标签组成的,其中LG是只计算相同类别对图片的损失函数,LI是只计算不相同类别对图片的损失函数。P是训练的样本数。通过这样分开设计,可以达到当我们要最小化损失函数的时候,可以减少相同类别对的能量,增加不相同对的能量。很简单直观的方法是实现这个的话,我们只要将LG设计成单调增加,让LI单调递减就可以了,但是我们要保证一个前提就是,不相同的图片对(image pairs)距离肯定要比相同图片对的距离大,那么就是要满足:

所以论文中用了一个
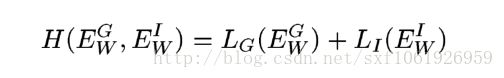
作为总的损失函数,可以满足这个condition1。论文中进行了各种假设的证明已经单调性的证明,这里不再重复。
最后给出一个精确的对单个样本的损失函数:
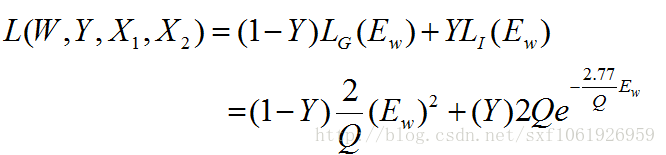
其中
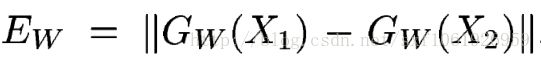
,Q是一个常量。
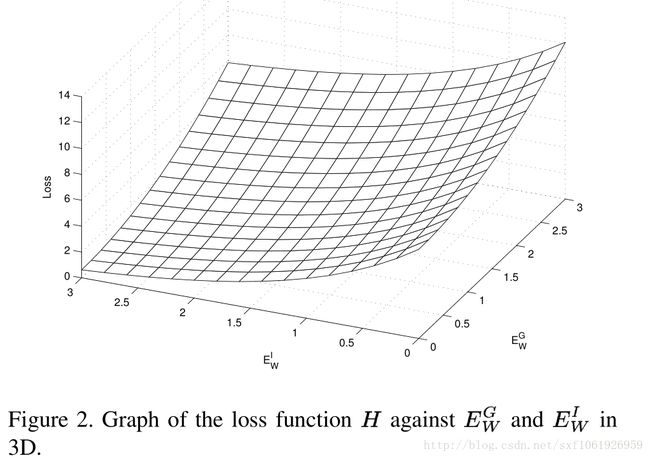
上图说明了收敛性。
总结思想
其实讲了这么多,主要思想就是三点:
1、输入不再是单个样本,而是一对样本,不再给单个的样本确切的标签,而且给定一对样本是否来自同一个类的标签,是就是0,不是就是1
2、设计了两个一模一样的网络,网络共享权值W,对输出进行了距离度量,可以说l1、l2等。
3、针对输入的样本对是否来自同一个类别设计了损失函数,损失函数形式有点类似交叉熵损失:
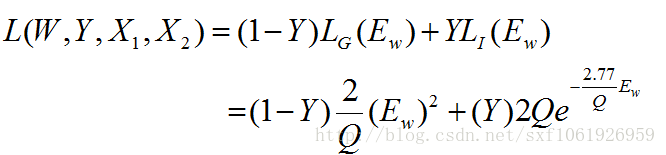
最后使用获得的损失函数,使用梯度反传去更新两个网络共享的权值W。
优点
这个网络主要的优点是淡化了标签,使得网络具有很好的扩展性,可以对那些没有训练过的类别进行分类,这点是优于很多算法的。而且这个算法对一些小数据量的数据集也适用,变相的增加了整个数据集的大小,使得数据量相对较小的数据集也能用深度网络训练出不错的效果。
实验设计
实验的时候要注意,输入数据最好打乱,由于这样去设计数据集后,相同类的样本对肯定比不相同的样本对数量少,在进行训练的时候最后将两者的数据量设置成相同数量。
总结
本文解释的只是最早提出的siamese网络结构,提出的是一种网络结构思想,具体的使用的网络形式完全可以自己定义。包括损失函数,相似度距离的定义等。比如将损失函数的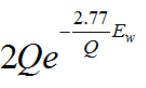 用hige loss代替等。
用hige loss代替等。
《Hamming Distance Metric Learning》这篇论文对siamese进一步改进,提出了一个triple net,主要贡献是将成对样本改成了三个样本,输入由(X1,X2,Y)变成了(X1,X2,X1’),表示X1和X1’是相同类别的样本,X1和x2是不同样本的类别。
《Learning to Compare Image Patches via Convolutional Neural Networks》这篇论文写得也很好,将两个网络进行合并,输入的成对标签直接同时输入同一个网络。
代码
使用tensorflow在mnist上实现的siamese net
参考文献2的官方code
参考文献
[1] S. Chopra, R. Hadsell, and Y. LeCun. Learning a similarity metric discriminatively, with application to face verification. In Computer Vision and Pattern Recognition, 2005. CVPR 2005. IEEE Computer Society Conference on, volume 1, pages 539–546. IEEE, 2005.
[2] Mohammad Norouzi, David J. Fleet, Ruslan Salakhutdinov, Hamming Distance Metric Learning, Neural Information Processing Systems (NIPS), 2012.
完