二、《Hands-On Machine Learning with Scikit-Learn and TensorFlow》一个完整的机器学习项目

 

本章中，你会假装作为被一家地产公司刚刚雇佣的数据科学家，完整地学习一个案例项目。
下面是主要步骤：
1. 项目概述。
2. 获取数据。
3. 发现并可视化数据，发现规律。
4. 为机器学习算法准备数据。
5. 选择模型，进行训练。
6. 微调模型。
7. 给出解决方案。
8. 部署、监控、维护系统。

---

2.1 使用真实数据集练手

本章选择了加州房价数据集，代码可以从https://github.com/ageron/handson-ml获取。

2.2 分析整体情况

我们的目的是使用加州的人口普查数据，建立模型，预测加州各区域的房价中位数。

训练数据的特征包括加州各区域的人口、收入中位数、房价中位数等。

2.2.1 问题构建（Frame the Problem，提出问题，给出框架，提出假设）

首先问清楚老板的商业目的，以及当前的解决方案（如果有的话）。比如，了解到了当前方案的错误率大概15%，我们就要奋斗目标了。

接下来就可以分析，这是一个有监督学习、无监督学习、还是增强学习？分类任务还是回归任务，或者别的什么？应该使用批量学习（batch learning）还是在线学习（online learning）？

如果数据量巨大，可以使用MapReduce技术，将数据分给多个服务器处理。也可是使用在线学习。

2.2.2 选择性能衡量指标（Select a Performance Measure） 

回归问题典型的衡量指标选择均方根误差（Root Mean Square Error，RMSE），它揭示了预测值的标准偏差（standard deviation）。例如，RMSE 等于 50000，意味着，68% 的系统预测值位于实际值的 50000 美元以内，95% 的预测值位于实际的 100000 美元以内（一个特征通常都符合高斯分布，即满足 “68-95-99.7”规则：大约68%的值落在 1σ  内，95% 的值落在 2σ  内，99.7%的值落在 3σ  内，这里的 σ  等于50000）。公式 2-1 展示了计算 RMSE 的方法。

 

有时候样本中存在很多离群点（outlier） ，我们可能就会使用绝对误差（Mean Absolute Error，MAE）。

 

RMSE和MAE都是向量距离的度量方式（预测值向量和目标值向量）。向量的距离，也可以为称为向量的模（norm），有以下性质：

• RMSE对应于欧氏距离，也被称作l2l2距离，记做∥⋅∥2‖⋅‖2（或∥⋅∥‖⋅‖）。
• MAE对应于l1l1距离，记做∥⋅∥1‖⋅‖1。
• 一般的，具有nn的元素的向量vv，lklk距离定义为∥v∥k=(|v1|k+|v2|k+⋯+|vn|k)1k‖v‖k=(|v1|k+|v2|k+⋯+|vn|k)1k。l0l0仅仅给出向量的基数（比如非零元素的个数），l∞l∞给出向量中最大元素的绝对值。
• 指数k最大，向量中最大元素的贡献就越大。这就是为什么相对于MAE，RMSE对离群点更敏感。但如果误差是指数级稀少（exponentially rare）的，例如钟形曲线（bell-shaped curve），RMSE的表现很好，也是通常的选择。

2.2.3 检查假设（Check the Assumptions） 

我们最好跟同事确认一下假设。例如，我们的房价预测值是给下游系统使用的。如果下游系统要把价格转换为类别（例如高、中、低），那么我们的问题就成了分类。

2.3 获取数据（Get the Data）

下面就开始动手操作了，代码位于https://github.com/ageron/handson-ml。

2.3.1 创建工作空间（Create the Workspace）

安装Python、安装Jupyter Notebook

2.3.2 下载数据

fetch_housing_data函数负责，代码里面有。

2.3.3 浏览数据（Take a Quick Look at the Data Structure）

介绍了pandas DataFrame里面的一些函数：

head()

可以查看数据是否成功导入，并可以查看数据包含哪些特征以及特征的形式大概是怎么样的。

 

info()输出每个特征的元素总个数以及类型信息等

info()可以查看每个特征的元素总个数，因此可以查看某个特征是否存在缺失值。还可以查看数据的类型以及内存占用情况。

可以看到total_bedrooms特征总个数为20433，而不是20640，所以存在缺失值。除了ocean_proximity为object类型（一般为一些文字label）以外，其余特征都为浮点型(float64)

 

value_counts()统计特征中每个元素的总个数，value_counts()一般用在统计有有限个元素的特征（如标签label，地区等）

describe()可以看实数特征的统计信息，describe()可以看实数特征的最大值、最小值、平均值、方差、总个数、25%，50%，75%小值。

 

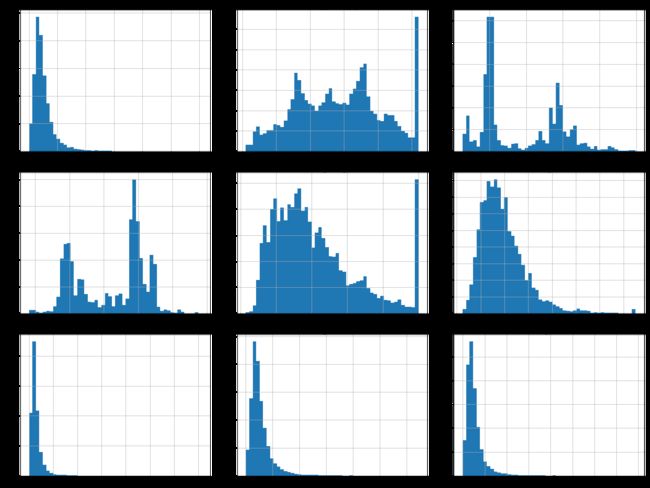
Matplotlib里面的hist()函数绘制直方图。

我们可以从直方图中发现以下几点：

1. 收入中位数（median income）并不是以美元为单位的，而是经过了预处理。最高一致被设置为了大概15（高于某一值的数据，都被设置为了15，即使它可能是25），最低值被设置为0.5（低于某一值的都被设置为0.5）。这在机器学习中很常见，也没什么问题。
2. 房龄中位数（housing median age）和房价中位数（median house value）也被处理过了。例如后者，房价高于500,000的，都被设置为500,000，即使真实房价800,000。这就是为什么它们所对应的直方图，最右列突然增高。但由于房价中位数是我们的目标属性，如果我们需要预测真实的房价，可能会高于500,000，这就存在问题了。那么有两种主要的解决方案：a、收集真实的房价。b、丢掉房价高于500,000的样本。
3. 这些属性具有不同的取值范围。这将在下文探索特征缩放是进行讨论。
4. 本多直方图呈现重尾分布（tail heavy）：左侧距离中位数要远于右侧。这不利于一些机器学习算法进行模式识别（tail heavy）。后面将进行转换，使这些属性更符合钟形分布（bell-shaped distributions）。

 

2.3.4 创建测试集

为了最终验证模型是否具有推广泛化能力，需要分开训练集于测试集，假设将数据集分为80%训练，20%测试。下面为一种普遍的分开数据集的代码：

import numpy as np
def split_train_test(data, test_ratio):
    shuffled_indices = np.random.permutation(len(data))
    test_set_size = int(len(data) * test_ratio)
    test_indices = shuffled_indices[:test_set_size]
    train_indices = shuffled_indices[test_set_size:]
    return data.iloc[train_indices], data.iloc[test_indices]
 
train_set, test_set = split_train_test(housing, 0.2)
print(len(train_set), "train +", len(test_set), "test")

这虽然能正确的分开训练、测试集，但是如果重新运行程序，训练和测试集会不一样。假设在原来模型的基础上继续训练，则不能保证测试集没有被模型训练过，因此不能验证模型效果。下面有两种方案：

  方案一：使用在shuffle之前（即permutation），调用np.random.seed(42)，则每次运行shuffle的结果一样（即训练、测试集一样）。但是如果新增加了一些数据集，则这个方案将不可用。

    方案二：为了解决方案一的问题，采用每个样本的识别码（可以是ID，可以是行号）来决定是否放入测试集，例如计算识别码的hash值，取hash值得最后一个字节（0~255），如果该值小于一个数（20% * 256）则放入测试集。这样，这20%的数据不会包含训练过的样本。

 

---

 

交叉验证(Cross-validation) 
交叉验证是指在给定的建模样本中，拿出其中的大部分样本进行模型训练，生成模型，留小部分样本用刚建立的模型进行预测，并求这小部分样本的预测误差，记录它们的平方加和。这个过程一直进行，直到所有的样本都被预测了一次而且仅被预测一次，比较每组的预测误差，选取误差最小的那一组作为训练模型。

StratifiedShuffleSplit函数的使用 
用法：

from  sklearn.model_selection import StratifiedShuffleSplit
StratifiedShuffleSplit(n_splits=10,test_size=None,train_size=None, random_state=None)

2.1 参数说明

参数 n_splits是将训练数据分成train/test对的组数，可根据需要进行设置，默认为10

参数test_size和train_size是用来设置train/test对中train和test所占的比例。例如： 
1.提供10个数据num进行训练和测试集划分 
2.设置train_size=0.8 test_size=0.2 
3.train_num=num*train_size=8 test_num=num*test_size=2 
4.即10个数据，进行划分以后8个是训练数据，2个是测试数据

注*：train_num≥2，test_num≥2 ;test_size+train_size可以小于1*

参数 random_state控制是将样本随机打乱

2.2 函数作用描述 
1.其产生指定数量的独立的train/test数据集划分数据集划分成n组。 
2.首先将样本随机打乱，然后根据设置参数划分出train/test对。 
3.其创建的每一组划分将保证每组类比比例相同。即第一组训练数据类别比例为2:1，则后面每组类别都满足这个比例

2.3 具体实现

from sklearn.model_selection import StratifiedShuffleSplit
import numpy as np
X = np.array([[1, 2], [3, 4], [1, 2], [3, 4],
              [1, 2],[3, 4], [1, 2], [3, 4]])#训练数据集8*2
y = np.array([0, 0, 1, 1,0,0,1,1])#类别数据集8*1

ss=StratifiedShuffleSplit(n_splits=5,test_size=0.25,train_size=0.75,random_state=0)#分成5组，测试比例为0.25，训练比例是0.75

for train_index, test_index in ss.split(X, y):
   print("TRAIN:", train_index, "TEST:", test_index)#获得索引值
   X_train, X_test = X[train_index], X[test_index]#训练集对应的值
   y_train, y_test = y[train_index], y[test_index]#类别集对应的值

运行结果： 

TRAIN: [5 2 6 4 1 3] TEST: [7 0]
TRAIN: [4 3 5 2 7 1] TEST: [6 0]
TRAIN: [7 1 6 2 0 4] TEST: [5 3]
TRAIN: [3 6 4 7 0 5] TEST: [1 2]
TRAIN: [3 4 1 7 2 0] TEST: [6 5]

简洁、方便的Scikit-Learn 也提供了相关的分开训练和测试集的函数。

---

当然，这种简单的划分方式并没有考虑到一些深层次的问题，如果数据集是分层抽样获取的，那么这样划分会打乱数据集原有的分层结构。下面我们新建一个特征，来帮助描述这个问题

#将收入除以1.5以避免收入跨度太大，再取上值
housing['income_cat'] = np.ceil(housing['median_income'] / 1.5)

#将income_cat中大于5的值全部转换成5
housing['income_cat'].where(housing['income_cat'] < 5, 5.0, inplace = True

from sklearn.model_selection import StratifiedShuffleSplit

split = StratifiedShuffleSplit(n_splits = 1, test_size = 0.2, random_state = 42)
for train_index, test_index in split.split(housing, housing['income_cat']):
    strat_train_set = housing.loc[train_index]
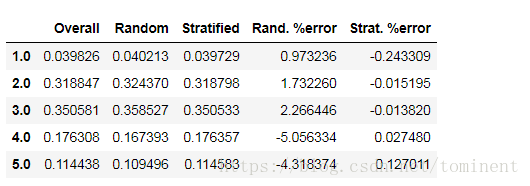
    strat_test_set = housing.loc[test_index]

对比了总数据集、分层采样的测试集、纯随机采样测试集的收入分类比例。可以看到，分层采样测试集的收入分类比例与总数据集几乎相同，而随机采样数据集偏差严重。

由于income_cat特征只是我们用于划分的特征，对训练没有任何作用，所以最后需要将加入的income_cat删除

for set in (strat_train_set, strat_test_set):
    set.drop(["income_cat"], axis=1, inplace=True)

 

---