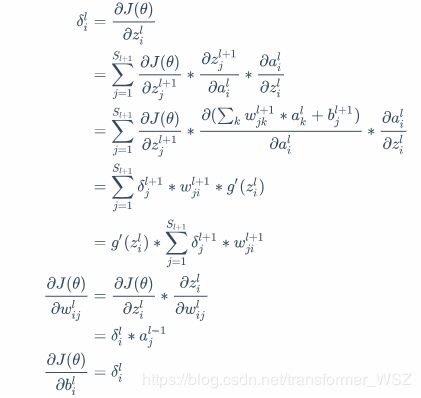反向传播
简介
误差反向传播算法简称反向传播算法(Back Propagation)。使用反向传播算法的多层感知器又称为BP神经网络。
BP算法是一个迭代算法,它的基本思想如下:
- 将训练集数据输入到神经网络的输入层,经过隐藏层,最后达到输出层并输出结果,这就是前向传播过程。
- 由于神经网络的输出结果与实际结果有误差,则计算估计值与实际值之间的误差,并将该误差从输出层向隐藏层反向传播,直至传播到输入层;
- 在反向传播的过程中,根据误差调整各种参数的值(相连神经元的权重),使得总损失函数减小。
- 迭代上述三个步骤(即对数据进行反复训练),直到满足停止准则。
示例
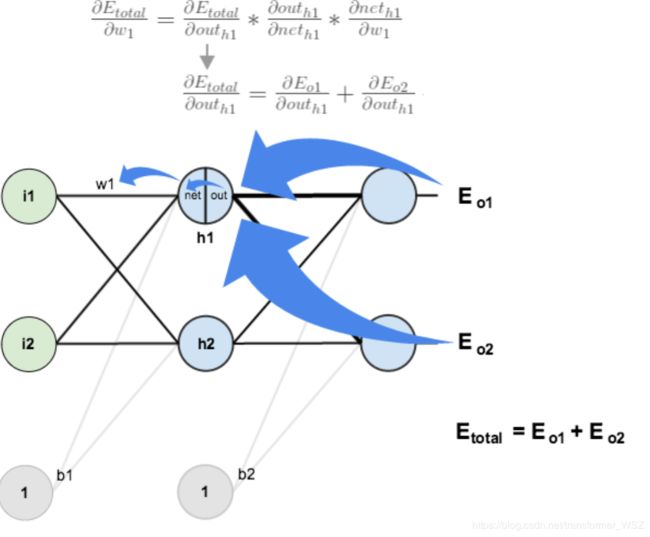
有如下一个神经网络:
第一层是输入层,包含两个神经元 i 1 i_1 i1, i 2 i_2 i2 和偏置项 b 1 b_1 b1;第二层是隐藏层,包含两个神经元 h 1 h_1 h1, h 2 h_2 h2 和偏置项 b 2 b_2 b2;第三层是输出 o 1 o_1 o1, o 2 o_2 o2。每条线上标的 w i w_i wi 是层与层之间连接的权重。激活函数是 s i g m o d sigmod sigmod 函数。我们用 z z z 表示某神经元的加权输入和;用 a a a 表示某神经元的输出。
上述各参数赋值如下:
| 参数 | 值 |
|---|---|
| i 1 i_1 i1 | 0.05 |
| i 2 i_2 i2 | 0.10 |
| w 1 w_1 w1 | 0.15 |
| w 2 w_2 w2 | 0.20 |
| w 3 w_3 w3 | 0.25 |
| w 4 w_4 w4 | 0.30 |
| w 5 w_5 w5 | 0.40 |
| w 6 w_6 w6 | 0.45 |
| w 7 w_7 w7 | 0.50 |
| w 8 w_8 w8 | 0.55 |
| b 1 b_1 b1 | 0.35 |
| b 2 b_2 b2 | 0.60 |
| o 1 o_1 o1 | 0.01 |
| o 2 o_2 o2 | 0.99 |
Step 1 前向传播
输入层 —> 隐藏层
神经元 h 1 h_1 h1 的输入加权和:
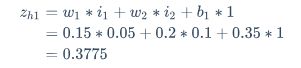
神经元 h 1 h_1 h1 的输出 a h 1 a_{h1} ah1 :
a h 1 = 1 1 + e − z h 1 = 1 1 + e − 0.3775 = 0.593269992 a_{h1} = \frac{1}{1+e^{-z_{h1}}} = \frac{1}{1+e^{-0.3775}} = 0.593269992 ah1=1+e−zh11=1+e−0.37751=0.593269992
同理可得,神经元 h 2 h_2 h2 的输出 a h 2 a_{h2} ah2 :
a h 2 = 0.596884378 a_{h2} = 0.596884378 ah2=0.596884378
隐藏层 —> 输出层
计算输出层神经元 o 1 o1 o1 和 o 2 o2 o2 的值:

前向传播的过程就结束了,我们得到的输出值是 [ 0.751365069 , 0.772928465 ] [0.751365069, 0.772928465] [0.751365069,0.772928465] ,与实际值 [ 0.01 , 0.99 ] [0.01, 0.99] [0.01,0.99] 相差还很远。接下来我们对误差进行反向传播,更新权值,重新计算输出。
Step 2 反向传播
- 计算损失函数:
E t o t a l = ∑ 1 2 ( t a r g e t − o u t p u t ) 2 E_{total} = \sum\frac{1}{2}(target - output)^2 Etotal=∑21(target−output)2
但是有两个输出,所以分别计算 o 1 o_1 o1 和 o 2 o_2 o2 的损失值,总误差为两者之和:
E o 1 = 1 2 ( 0.01 − 0.751365069 ) 2 = 0.274811083 E o 2 = 1 2 ( 0.99 − 0.772928465 ) 2 = 0.023560026 E t o t a l = E o 1 + E o 2 = 0.274811083 + 0.023560026 = 0.298371109 E_{o_1} = \frac {1}{2}(0.01 - 0.751365069)^2 = 0.274811083 \\ E_{o_2} = \frac {1}{2}(0.99 - 0.772928465)^2 = 0.023560026 \\ E_{total} = E_{o_1} + E_{o_2} = 0.274811083 + 0.023560026 = 0.298371109 Eo1=21(0.01−0.751365069)2=0.274811083Eo2=21(0.99−0.772928465)2=0.023560026Etotal=Eo1+Eo2=0.274811083+0.023560026=0.298371109
- 隐藏层 —> 输出层的权值更新
以权重参数 w 5 w_5 w5 为例,如果我们想知道 w 5 w_5 w5 对整体损失产生了多少影响,可以用整体损失对 w 5 w_5 w5 求偏导:
∂ E t o t a l ∂ w 5 = ∂ E t o t a l ∂ a o 1 ∗ ∂ a o 1 ∂ z o 1 ∗ ∂ z o 1 ∂ w 5 \frac{\partial E_{total}}{\partial w_5} = {\frac {\partial E_{total}}{\partial a_{o_1}}}*{\frac {\partial a_{o_1}}{\partial z_{o_1}} }*{ \frac {\partial z_{o_1}} {\partial w_5} } ∂w5∂Etotal=∂ao1∂Etotal∗∂zo1∂ao1∗∂w5∂zo1
下面的图可以更直观了解误差是如何反向传播的:
我们现在分别来计算每个式子的值:
计算 ∂ E t o t a l ∂ a o 1 \frac {\partial E_{total}} {\partial a_{o_1}} ∂ao1∂Etotal :
E t o t a l = 1 2 ( t a r g e t o 1 − a o 1 ) 2 + 1 2 ( t a r g e t o 2 − a o 1 ) 2 ∂ E t o t a l ∂ a o 1 = 2 ∗ 1 2 ( t a r g e t o 1 − a o 1 ) ∗ − 1 ∂ E t o t a l ∂ a o 1 = − ( t a r g e t o 1 − a o 1 ) = 0.751365069 − 0.01 = 0.741365069 E_{total} = \frac {1}{2}(target_{o_1} - a_{o_1})^2 + \frac {1}{2}(target_{o_2} - a_{o_1})^2 \\ \frac {\partial E_{total}} {\partial a_{o_1}} = 2 * \frac {1}{2} (target_{o_1} - a_{o_1})*-1 \\ \frac {\partial E_{total}} {\partial a_{o_1}} = -(target_{o_1} - a_{o_1}) = 0.751365069-0.01=0.741365069 \\ Etotal=21(targeto1−ao1)2+21(targeto2−ao1)2∂ao1∂Etotal=2∗21(targeto1−ao1)∗−1∂ao1∂Etotal=−(targeto1−ao1)=0.751365069−0.01=0.741365069
计算 ∂ E t o t a l ∂ a o 1 \frac {\partial E_{total}} {\partial a_{o_1}} ∂ao1∂Etotal :
a o 1 = 1 1 + e − z o 1 ∂ a o 1 ∂ z o 1 = a o 1 ∗ ( 1 − a o 1 ) = 0.751365069 ∗ ( 1 − 0.751365069 ) = 0.186815602 a_{o_1} = \frac {1}{1+e^{-z_{o_1}}} \\ \frac {\partial a_{o_1}} {\partial z_{o_1}} = a_{o_1}*(1-a_{o_1}) = 0.751365069*(1-0.751365069) = 0.186815602 ao1=1+e−zo11∂zo1∂ao1=ao1∗(1−ao1)=0.751365069∗(1−0.751365069)=0.186815602
计算 ∂ z o 1 ∂ w 5 \frac {\partial z_{o_1}} {\partial w_5} ∂w5∂zo1 :
z o 1 = w 5 ∗ a h 1 + w 6 ∗ a h 2 + b 2 ∗ 1 ∂ z o 1 ∂ w 5 = a h 1 = 0.593269992 z_{o_1} = w_5*a_{h1} + w_6*a_{h2} + b_2*1 \\ \frac {\partial z_{o_1}} {\partial w_5} = a_{h_1} = 0.593269992 zo1=w5∗ah1+w6∗ah2+b2∗1∂w5∂zo1=ah1=0.593269992
最后三者相乘:
∂ E t o t a l ∂ w 5 = 0.741365069 ∗ 0.186815602 ∗ 0.593269992 = 0.082167041 \frac {\partial E_{total}} {\partial w_5} = 0.741365069*0.186815602*0.593269992 = 0.082167041 ∂w5∂Etotal=0.741365069∗0.186815602∗0.593269992=0.082167041
这样我们就算出整体损失 E t o t a l E_{total} Etotal 对 w 5 w_5 w5 的偏导值。
∂ E t o t a l ∂ w 5 = − ( t a r g e t o 1 − a o 1 ) ∗ a o 1 ∗ ( 1 − a o 1 ) ∗ a h 1 \frac {\partial E_{total}} {\partial w_5} = -(target_{o_1} - a_{o_1}) * a_{o_1}*(1-a_{o_1}) * a_{h_1} ∂w5∂Etotal=−(targeto1−ao1)∗ao1∗(1−ao1)∗ah1
针对上述公式,为了表达方便,使用 δ o 1 \delta_{o_1} δo1 来表示输出层的误差:
δ o 1 = ∂ E t o t a l ∂ a o 1 ∗ ∂ a o 1 ∂ z o 1 = ∂ E t o t a l ∂ z o 1 δ o 1 = − ( t a r g e t o 1 − a o 1 ) ∗ a o 1 ∗ ( 1 − a o 1 ) \delta_{o_1} = {\frac {\partial E_{total}}{\partial a_{o_1}}}*{\frac {\partial a_{o_1}}{\partial z_{o_1}} } = \frac {\partial E_{total}} {\partial z_{o_1}} \\ \delta_{o_1} = -(target_{o_1} - a_{o_1}) * a_{o_1}*(1-a_{o_1}) δo1=∂ao1∂Etotal∗∂zo1∂ao1=∂zo1∂Etotalδo1=−(targeto1−ao1)∗ao1∗(1−ao1)
因此整体损失 E t o t a l E_{total} Etotal 对 w 5 w_5 w5 的偏导值可以表示为:
∂ E t o t a l ∂ w 5 = δ o 1 ∗ a h 1 \frac {\partial E_{total}}{\partial w_5} = \delta_{o_1}*a_{h_1} ∂w5∂Etotal=δo1∗ah1
最后我们来更新 w 5 w_5 w5 的值:
w 5 + = w 5 − η ∗ ∂ E t o t a l ∂ w 5 = 0.4 − 0.5 ∗ 0.082167041 = 0.35891648 η : 学 习 率 w_5^+ = w_5 - \eta * \frac {\partial E_{total}} {\partial w_5} = 0.4 - 0.5*0.082167041 = 0.35891648 \qquad \eta: 学习率 w5+=w5−η∗∂w5∂Etotal=0.4−0.5∗0.082167041=0.35891648η:学习率
同理可更新 w 6 , w 7 , w 8 w_6, w_7, w_8 w6,w7,w8 :
w 6 + = 0.408666186 w 7 + = 0.511301270 w 8 + = 0.561370121 w_6^+ = 0.408666186 \\ w_7^+ = 0.511301270 \\ w_8^+ = 0.561370121 w6+=0.408666186w7+=0.511301270w8+=0.561370121
- 隐藏层 —> 隐藏层的权值更新:
计算 ∂ E t o t a l ∂ w 1 \frac {\partial E_{total}} {\partial w_1} ∂w1∂Etotal 与上述方法类似,但需要注意下图:
计算 ∂ E t o t a l ∂ a h 1 \frac {\partial E_{total}} {\partial a_{h_1}} ∂ah1∂Etotal :
∂ E t o t a l ∂ a h 1 = ∂ E o 1 ∂ a h 1 + ∂ E o 2 ∂ a h 1 \frac {\partial E_{total}} {\partial a_{h_1}} = \frac {\partial E_{o_1}} {\partial a_{h_1}} + \frac {\partial E_{o_2}} {\partial a_{h_1}} ∂ah1∂Etotal=∂ah1∂Eo1+∂ah1∂Eo2
先计算 ∂ E o 1 ∂ a h 1 \frac {\partial E_{o_1}} {\partial a_{h_1}} ∂ah1∂Eo1 :
同理可得:
∂ E o 2 ∂ a h 1 = − 0.019049119 \frac {\partial E_{o_2}} {\partial a_{h_1}} = -0.019049119 ∂ah1∂Eo2=−0.019049119
两者相加得:
∂ E t o t a l ∂ a h 1 = 0.055399425 − 0.019049119 = 0.036350306 \frac {\partial E_{total}} {\partial a_{h_1}} = 0.055399425 - 0.019049119 = 0.036350306 ∂ah1∂Etotal=0.055399425−0.019049119=0.036350306
计算 a h 1 z h 1 \frac {a_{h_1}} {z_{h_1}} zh1ah1 :
a h 1 z h 1 = a h 1 ∗ ( 1 − a h 1 ) = 0.593269992 ∗ ( 1 − 0.593269992 ) = 0.2413007086 \frac {a_{h_1}} {z_{h_1}} = a_{h_1} * (1-a_{h_1}) = 0.593269992*(1-0.593269992) = 0.2413007086 zh1ah1=ah1∗(1−ah1)=0.593269992∗(1−0.593269992)=0.2413007086
计算 ∂ z h 1 ∂ w 1 \frac {\partial z_{h_1}} {\partial w_1} ∂w1∂zh1
∂ z h 1 ∂ w 1 = i 1 = 0.05 \frac {\partial z_{h_1}} {\partial w_1} = i_1 = 0.05 ∂w1∂zh1=i1=0.05
最后三者相互乘:
∂ E t o t a l ∂ w 1 = 0.036350306 ∗ 0.2413007086 ∗ 0.05 = 0.000438568 \frac {\partial E_{total}} {\partial w_1} = 0.036350306 * 0.2413007086 * 0.05 = 0.000438568 ∂w1∂Etotal=0.036350306∗0.2413007086∗0.05=0.000438568
为了简化公式,用 δ h 1 \delta_{h_1} δh1 表示隐藏层单元 h 1 h_1 h1 的误差:
最后更新 w 1 w_1 w1 的权值:
w 1 + = w 1 − η ∗ ∂ E t o t a l ∂ w 1 = 0.15 − 0.5 ∗ 0.000438568 = 0.149780716 w_1^+ = w_1 - \eta * \frac {\partial E_{total}} {\partial w_1} = 0.15 - 0.5*0.000438568 = 0.149780716 w1+=w1−η∗∂w1∂Etotal=0.15−0.5∗0.000438568=0.149780716
同理,更新 w 2 , w 3 , w 4 w_2, w_3, w_4 w2,w3,w4 权值:
w 2 + = 0.19956143 w 3 + = 0.24975114 w 4 + = 0.29950229 w_2^+ = 0.19956143 \\ w_3^+ = 0.24975114 \\ w_4^+ = 0.29950229 w2+=0.19956143w3+=0.24975114w4+=0.29950229
这样,反向传播算法就完成了,最后我们再把更新的权值重新计算,不停地迭代。在这个例子中第一次迭代之后,总误差 E t o t a l E_{total} Etotal 由0.298371109下降至0.291027924。迭代10000次后,总误差为0.000035085,输出为 [ 0.015912196 , 0.984065734 ] ( 原 输 入 为 [ 0.01 , 0.99 ] [0.015912196,0.984065734](原输入为[0.01,0.99] [0.015912196,0.984065734](原输入为[0.01,0.99] ,证明效果还是不错的。
公式推导
符号说明
| 符号 | 说明 |
|---|---|
| n l n_l nl | 网络层数 |
| y j y_j yj | 输出层第 j j j 类标签 |
| S l S_l Sl | 第 l l l 层神经元个数(不包括偏置项) |
| g ( x ) g(x) g(x) | 激活函数 |
| w i j l w_{ij}^{l} wijl | 第 l − 1 l-1 l−1 层的第 j j j 个神经元连接到第 l l l 层第 i i i 个神经元的权重 |
| b i l b_i^{l} bil | 第 l l l 层的第 i i i 个神经元的偏置 |
| z i l z_i^{l} zil | 第 l l l 层的第 i i i 个神经元的输入加权和 |
| a i l a_i^{l} ail | 第 l l l 层的第 i i i 个神经元的输出(激活值) |
| δ i l \delta_i^{l} δil | 第 l l l 层的第 i i i 个神经元产生的错误 |
推导过程
基本公式
梯度方向传播公式推导
初始条件
递推公式
反向传播伪代码
- 输入训练集。
- 对于训练集的每个样本 x ⃗ \vec x x ,设输入层对应的激活值为 a l a^l al :
- 前向传播: z l = w l ∗ a l − 1 + b l , a l = g ( z l ) z^l = w^l*a^{l-1}+b^l, a^l = g(z^l) zl=wl∗al−1+bl,al=g(zl)
- 计算输出层产生的误差: δ L = ∂ J ( θ ) ∂ a L ⊙ g ′ ( z L ) \delta^L = \frac {\partial J(\theta)} {\partial a^L} \odot g'(z^L) δL=∂aL∂J(θ)⊙g′(zL)
- 反向传播错误: δ l = ( ( w l + 1 ) T ∗ δ l + 1 ) ⊙ g ′ ( z l ) \delta^l = ((w^{l+1})^T*\delta^{l+1}) \odot g'(z^l) δl=((wl+1)T∗δl+1)⊙g′(zl)
- 使用梯度下降训练参数:
- w l ⇢ w l − α m ∑ x δ x , l ∗ ( a x , l − 1 ) T w^l \dashrightarrow w^l - \frac {\alpha} {m} \sum_x\delta^{x, l}*(a^{x, l-1})^T wl⇢wl−mα∑xδx,l∗(ax,l−1)T
- b l ⇢ b l − η m ∑ x δ x , l b^l \dashrightarrow b^l - \frac {\eta} {m} \sum_x\delta^{x, l} bl⇢bl−mη∑xδx,l
交叉熵损失函数推导
对于多分类问题, s o f t m a x softmax softmax 函数可以将神经网络的输出变成一个概率分布。它只是一个额外的处理层,下图展示了加上了 s o f t m a x softmax softmax 回归的神经网络结构图:
递推公式仍然和上述递推公式保持一致。初始条件如下:
s o f t m a x softmax softmax 偏导数计算:
∂ y j p ∂ a i n l = { − y i p ∗ y j p i ≠ j y i p ∗ ( 1 − y i p ) i = j \frac {\partial y_j^p} {\partial a_i^{nl}} = \left\{ \begin{aligned} -y_i^p*y_j^p \qquad i \neq j \\ y_i^p*(1-y_i^p) i = j \end{aligned} \right. ∂ainl∂yjp={−yip∗yjpi̸=jyip∗(1−yip)i=j
推导过程
参考自:
- https://www.cnblogs.com/charlotte77/p/5629865.html?tdsourcetag=s_pcqq_aiomsg
- https://blog.csdn.net/u014313009/article/details/51039334
- https://www.cnblogs.com/nowgood/p/backprop2.html?tdsourcetag=s_pcqq_aiomsg