A-02 梯度下降法

更新、更全的《机器学习》的更新网站，更有python、go、数据结构与算法、爬虫、人工智能教学等着你：https://www.cnblogs.com/nickchen121/p/11686958.html

梯度下降法

在求解机器学习算法模型参数的时候，梯度下降法（gradient descent）和最小二乘法（least squares）是最经常使用的方法，由于梯度下降法衍生出的分支较多，所以在这里对梯度下降法单独做一个总结。

一、梯度下降法详解

1.1 梯度

梯度是在微积分中对多元函数的各个参数求偏导数，并且把求得的各个参数的偏导数用向量的形式表达出来。

例如函数\(L(\omega,b)\)，分别对\(\omega\)和\(b\)求偏导数，梯度向量就是\(({\frac{\partial{L}}{\partial{\omega}}},{\frac{\partial{L}}{\partial{b}}})^T\)，简称\(grad{L(\omega,b)}\)或者\(\nabla{L(\omega,b)}\)。对于某个具体的点\((\omega_i,b_i)\)的具体梯度向量就是\(({\frac{\partial{L}}{\partial{\omega_i}}},{\frac{\partial{L}}{\partial{b_i}}})^T\)或者\(\nabla{L(\omega_i,b_i)}\)，如果是多参数的函数则是\(({\frac{\partial{L}}{\partial{x}}},{\frac{\partial{L}}{\partial{y}}},{\frac{\partial{L}}{\partial{z}}})^T\)。

1.2 梯度下降法和梯度上升法

在机器学习算法中，如果需要最小化目标函数时，则可以通过梯度下降法一步一步的迭代求解，得到最小化的目标函数和模型参数值；如果要最大化目标函数时，则可以通过梯度上升法迭代求解。

梯度下降算法和梯度上升法之间也可以互相转化，可以通过梯度下降迭代最小化目标函数，同时也可以反向梯度上升迭代最小化目标函数；同理也可以反向梯度下降迭代最大化目标函数。

1.3 梯度下降

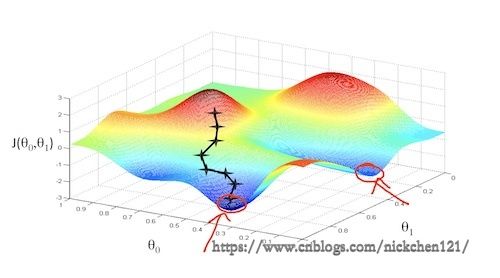
假设我们处在某座不知名的大山上的某处位置，由于我们不知道该怎么下山，于是决定走一步算一步，即每走到一个位置的时候便求解当前位置的梯度，沿着梯度的负方向即当前最陡峭的位置向下走一步，然后继续求解当前位置的梯度……直到我们认为我们已经到了山脚才停下来。从下图可以看出，通过该方法我们有可能走到了这座大山的某一个局部的最低处(山腰处)，而没有走到真正的山脚。

从下山这个实例中可以得出：梯度下降不一定能够找到全局的最优解，有可能会找到局部最优解。

但是如果代价函数为凸函数的时候梯度下降得到的则一定是全局最优解。

1.4 相关概念

1.4.1 步长

步长决定了梯度下降迭代的时候每一步沿梯度负方向前进的长度，下山实例中则表示每一步的长度。

如果步长过长，则可能会错过最优解；如果步长过小，迭代速度会变慢，很长时间算法都不会结束。因此可以从大到小的尝试步长的大小，如果目标函数值在变小，说明取值有效，否则需要增大步长。

1.4.2 假设函数

以线性模型举例，线性模型的假设函数为预测值的预测函数，即通过输入特征\((x_1,x_2,\ldots,x_n)\)输出一个对应的预测值\(\hat{y}\)，线性模型的假设函数为
\[ \hat{y} = f(x) = \omega_1x_1 + \omega_2x_2 + \cdots + \omega_nx_n + b \]

1.4.3 目标函数

目标函数常用来度量模型拟合的程度，以线性模型举例，线性模型一般使用均方误差度量模型性能，线性模型的目标函数为
\[ J(\omega,b) = \sum_{i=1}^m (y_i - \hat{y_{i}})^2 \]

二、梯度下降法流程

2.1 梯度下降法——代数法

假设现有一个目标函数\(J(\omega_0,\omega_1,\ldots,\omega_n)\)。

1. 初始化参数\(\omega_0=0,\omega_1=0,\ldots,\omega_n=0\)，也可以初始化成趋近于\(0\)的较小值；自定义步长\(\alpha=1\)；自定义阈值\(\epsilon\)
2. 计算当前位置的目标函数的梯度\({\frac{\partial}{\partial{\omega_i}}J(\omega_0,\omega_1,\ldots,\omega_n)}\)
3. 使用步长乘以目标函数的梯度得\(\alpha{\frac{\partial}{\partial{\omega_i}}J(\omega_0,\omega_1,\ldots,\omega_n)}\)
4. 如果所有的\(\omega_i\)的梯度下降的距离都小于阈值，则算法停止，当前的\(\omega_0,\omega_1,\ldots,\omega_n\)即为最终结果；否则继续下一步
5. 更新所有的\(\omega\)，更新公式为\(\omega_i = \omega_i - \alpha{\frac{\partial}{\partial{\omega_i}}J(\omega_0,\omega_1,\ldots,\omega_n)}\)更新成功后从步骤2继续开始

2.2 梯度下降法——矩阵法

这一部分主要用到了矩阵的基本计算和求导，首先对假设函数和目标函数矩阵化。

假设现有一个假设函数
\[ \hat{y} = \omega_1x_1 + \omega_2x_2 + \cdots + \omega_nx_n + b = X^T\omega \]
其中\(X^T\omega\)是假设函数的矩阵表达（把\(b\)看做\(\omega_0x_0, \quad x_0=1\)），其中\(X^T\)是\(m*(n+1)\)维的特征矩阵（\(m\)为样本数，\(n\)为特征数），\(\omega\)是\((n+1)*1\)维的向量，则通过矩阵的计算得知\(X^T\omega\)是一个\(m*1\)维的向量。

假设函数的转换即可得矩阵表达的目标函数，即
\[ J(\theta)={\frac{1}{2}}(X\omega-Y)^T(X\omega-Y) \]
其中\(Y\)是\(m*1\)维的样本向量。

1. 初始化向量\(\omega\)的每个元素为0，也可以初始化成趋近于\(0\)的较小值；自定义步长\(\alpha=1\)；自定义阈值\(\epsilon\)
2. 计算当前位置的目标函数的梯度，对于向量\(\omega\)，其梯度表达式为\({\frac{\partial}{\partial\omega}}J(\omega)\)
3. 使用步长乘以目标函数的梯度得\(\alpha{\frac{\partial}{\partial\omega}}J(\omega)\)
4. 如果向量\(\omega\)内的每个元素都梯度下降的距离都小于阈值，则算法停止，当前的\(\omega\)即为最终结果；否则继续下一步
5. 更新所有的\(\omega\)，更新公式为\(\omega = \omega - \alpha{\frac{\partial}{\partial\omega}}J(\omega)\)更新成功后从步骤2继续开始

2.3 三种不同形式的梯度下降法

三种不同形式的梯度下降法步骤都是相同的，只是在更新参数的时候选择的样本数量不同，如果不关心样本数量，梯度下降法的更新公式为
\[ \omega_i = \omega_i - \alpha{\frac{\partial}{\partial{\omega_i}}J(\omega_0,\omega_1,\ldots,\omega_n)} \]
接下来的参数更新公式以均方误差线性回归模型举例，均方误差线性回归模型的目标函数对参数\(\omega\)的求偏导公式为
\[ \nabla{L(\omega_i)}=\sum_{j=0}^m(\hat{y_j}-y_j){x_i}^{(j)} \]
其中\(m\)是样本数，\({x_j}^{i}\)是第\(j\)个样本的第\(i\)个特征。

2.3.1 批量梯度下降法

批量梯度下降法（batch gradient descent）是最常用的做法，它使用所有的样本更新参数，它的参数更新公式为
\[ \omega_i = \omega_i - \alpha\sum_{j=0}^m(\hat{y_j}-y_j){x_i}^{(j)} \]

2.3.2 随机梯度下降法

随机梯度下降法（stochastic gradient descent）类似于批量梯度下降法，但是它随机的使用第\(j\)个样本更新参数，它的参数更新公式为
\[ \omega_i = \omega_i - \alpha(\hat{y_j}-y_j){x_i}^{(j)} \]

2.3.3 小批量梯度下降法

小批量梯度下降法（mini-batch gradient descent）属于批量下降法和随机梯度下降法的折中方法，即对于\(m\)样本，随机选定\(x\)个样本更新参数，一般\(x=10\)。假设这\(x\)样本的集合为\(D\)，它的参数更新公式为
\[ \omega_i = \omega_i - \alpha\sum_{j\in{D}} (\hat{y_j}-y_j){x_i}^{(j)} \]

批量梯度下降法使用所有的样本更新参数，计算量大，准确度高，但是更新速度慢。

随机梯度下降法随机使用一个样本更新参数，计算量小，更新速度快，但是准确度不高，并且由于使用一个样本更新参数，算法收敛速度慢。

小批量梯度下降法属于批量梯度下降法和随机梯度下降法的折中方法，但是采用的错误样本数需要具体问题去分析，否则采用错误的样本数量容易导致更新速度慢而且准确度也不高。

三、梯度下降法优缺点

3.1 优点

1. 如果目标函数是凸函数，可以获得全局最小值
2. 样本量很大的时候可以选择随机梯度下降法或者小批量梯度下降法，相对于最小二乘法灵活
3. 迭代时间相较于牛顿法更快

3.2 缺点

1. 步长需要人为控制，如果步长小了则目标函数收敛速度会变慢；步长大了容易错过最优解
2. 初始值设定不同获得的最小值也有可能不同，即梯度下降法只能获得局部最小值