轻量级网络--MobileNetV2论文解读

MobileNetV2

Inverted Residuals and Linear Bottlenecks: Mobile Networks for Classification, Detection and Segmentation

原文地址：MobileNetV2

非官方代码:

• github-mxnet
• github-PyTorch

---

Abstract

本文提出了一种新的移动架构MobileNetv2,改善了多个任务和基准的State-of-the-art水平。同时我们介绍了一种基于此框架的面向目标检测任务的有效应用模型SSDLite。此外，我们介绍了简化移动语义分割模型DeepLabv3构建新的Mobile DeepLabv3.

MobileNetv2架构是基于倒置残差结构(inverted residual structure)，原本的残差结构的主分支是有三个卷积，两个逐点卷积通道数较多，而倒置的残差结构刚好相反，中间的卷积通道数(依旧使用深度分离卷积结构)较多，旁边的较小。此外，我们发现去除主分支中的非线性变换是有效的，这可以保持模型表现力。论文在ImageNet classification, COCO object detection, VOC image segmentation上做了对比实验，验证了该架构的有效性。

---

Introduction

现代先进网络需要的高计算资源超出了移动和嵌入式设备的能力。本文针对这一资源限制条件设计了一套新的神经网络架构，该架构能在保持类似精度的条件下显著的减少模型参数和计算量。

论文的主要贡献在于提出一种新型层结构： 具有线性瓶颈的倒残差结构(the inverted residual with linear bottleneck)。

该模块首先将输入的低维压缩表示(low-dimensional compressed representation)扩展到高维，使用轻量级深度卷积做过滤；随后用linear bottleneck将特征投影回低维压缩表示。 这个模块可以使用任何现代框架中。此外，该模块特别适用于移动设备设计，它在推理过程不实现大的张量，这减少了需要嵌入式硬件设计对主存储器访问的需求。

---

Related Work

调整深度神经网络在精度和性能之间取得一个最佳平衡，是近几年的热门话题。 许多工作致力于方向可分为：

• 改进先进模型达到更加性能；
• 超参数调优以及各种网络修剪方法和连通性学习；
• 改变内容卷积块的联通结构，例如ShuffleNet引入稀疏性等。
• 最近，也有一个新方向将包括遗传算法和强化学习在内的优化算法引入，这使得得到的模型非常复杂。

我们追求的是找到关于神经网络操作使用的发展方向，这可以更简易的指导网络设计。我们的网络设计基于MobileNetV1的，保留了该模型的简单性，显著的提高了其准确性，达到了针对移动应用的分类和检测应用的先进水平。

---

初步，讨论和直觉(Preliminaries, discussion and intuition)

深度分离卷积(Depthwise Separable Convolutions)

将标准卷积拆分为深度分离卷积在MobileNetv1中详细讲解过了，其基本思想：将标准卷积拆分为两个分卷积：第一层称为深度卷积(depthwise convolution)，对每个输入通道应用单通道的轻量级滤波器；第二层称为逐点卷积(pointwise convolution)，负责计算输入通道的线性组合构建新的特征。

标准卷积$L_i$为$h_i\times w_i\times d_i$，应用标准卷积核$K\in R^{k\times k\times d_i\times d_j}$产生输出$L_j$为$h_i\times w_i\times d_j$.

• 标准卷积的计算消耗为：$h_i\cdot w_i\cdot d_i\cdot d_j\cdot k\cdot k$.
• 拆分后深度分离卷积计算消耗为：$h_i\cdot w_i\cdot d_i(k^2+d_j)$，计算消耗比例因子$\frac{k^2d_j}{k2+d_j} $

MobileNetv2中使用的卷积核大小$k=3$，与标准卷积相比计算量减少了8~9倍，精度上有略微的损失。

Linear Bottlenecks

这部分是论文的主要Insight了,我觉得比较难的理解，这里贴出我自己的看法~

我们认为深度神经网络是由$n$个$L_i$层构成，每层经过激活输出的张量为$h_i\times w_i\times d_i$。我们认为一连串的卷积和激活层形成一个**兴趣流形(manifold of interest，这就是我们感兴趣的数据内容)**，现阶段还无法定量的描述这种流行，这里以经验为主的研究这些流行性质。

长期以来我们认为：在神经网络中兴趣流行可以嵌入到低维子空间，通俗点说，我们查看的卷积层中所有单个d通道像素时，这些值中存在多种编码信息，兴趣流行位于其中的。我们可以通过变换，进一步嵌入到下一个低维子空间中(例如通过$1\times 1$卷积变换维数，转换兴趣流行所在空间维度)。

乍一看，这样的想法比较容易验证，可通过减少层维度从而降低激活空间的维度。MobileNetv1是通过宽度因子(width factor)在计算量和精度之间取折中。用上面的理论来说，宽度因子控制激活空间的维度，直到兴趣流行横跨整个空间。

然而，由于深度卷积神经网络的层是具有非线性激活函数的。以ReLU变换($F(x)=max(0,x)$)为例，会存在以下问题：

• 如果当前激活空间内兴趣流行完整度较高，经过ReLU，可能会让激活空间坍塌，不可避免的会丢失信息。(如下Figure 1的示意图)
• 如果经过ReLU变换输出是非零的，那输入和输出之间是做了一个线性变换的，即将输入空间中的一部分映射到全维输出，换句话来说，ReLU的作用是线性分类器。

下图展现了兴趣流行的变换示例:

Input是一张2维数据，其中兴趣流行是蓝色的螺纹线；本例使用矩阵$T$将数据嵌入到$n$维空间中，后接ReLU，再使用$T^{-1}$将其投影回2D平面。

可以看到设置$n=2,3$时信息丢失严重，中心点坍塌掉了。当$n=15..30$之间，恢复的信息明显多了。

总结一下，我们强调了两个性质:

• 如果兴趣流行经过ReLU变换后得到非零的结果，这时ReLU对应着是一个线性变换
• 只有当输入流行可包含在输入空间的低维子空间中，ReLU才能完整的保持输入流行的信息。

存在的问题： 我们想要兴趣流行存在低维空间中，即想要提升效果，维度是要低一点。但是维度如果低的话，激活变换ReLU函数可能会滤除很多有用信息，而ReLU对于没有滤除的部分，即非零的部分的作用是一个线性分类器。

既然在低维空间中使用ReLU做激活变换会丢失很多信息，论文针对这个问题使用linear bottleneck(即不使用ReLU激活，做了线性变换)的来代替原本的非线性激活变换。到此，优化网络架构的思路也出来了：通过在卷积模块中后插入linear bottleneck来捕获兴趣流行。 实验证明，使用linear bottleneck可以防止非线性破坏太多信息。
(附录中说了一个看法： 如果输入流行可通过激活空间嵌入到显著的低维子空间，那么通常ReLU变换可保留信息，同时为所需的复杂性引入一组可表达的函数.我看的不是很懂，要表达的是ReLU的必要性~)

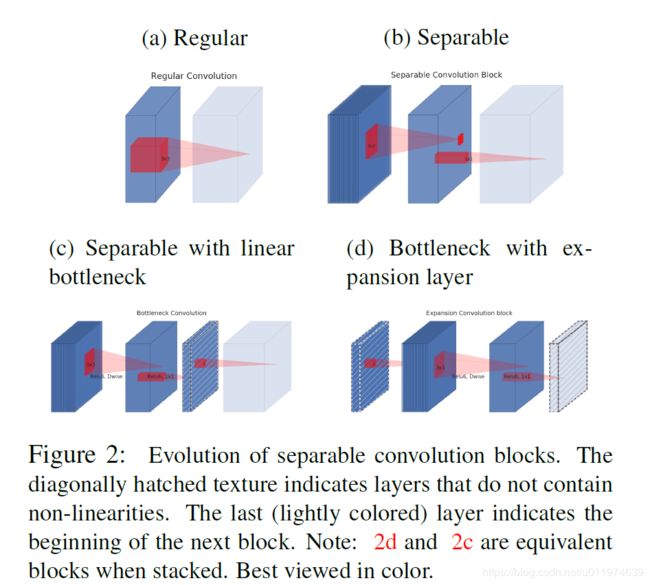
从linear bottleneck到深度卷积之间的的维度比称为Expansion factor(扩展系数),该系数控制了整个block的通道数。 linear bottleneck的使用操作的流程演化图如下：

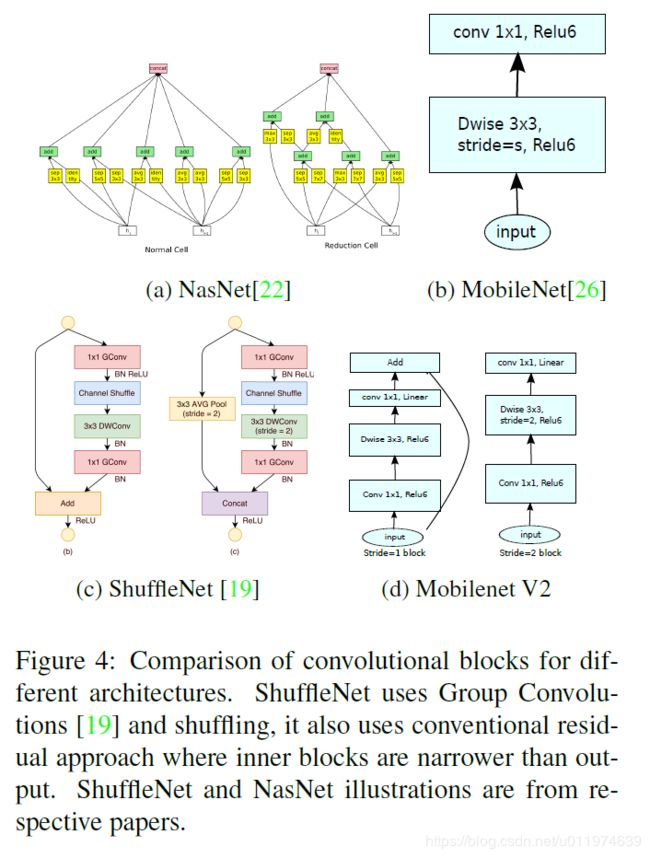
• 图(a)：普通模型架构使用标准卷积将空间和通道信息一起映射到下一层，参数和计算量会比较大
• 图(b)，MobileNetv1中将标准卷积拆分为深度卷积和逐点卷积，深度卷积负责逐通道的过滤空间信息，逐点卷积负责映射通道。将空间和通道分开了
• 图©和图(d)是MobileNetv2的结构(d是c的下一个连接状态)，同样是将标准卷积拆分为深度卷积和逐点卷积，在逐点卷积后使用了接$1\times 1$卷积，该卷积使用线性变换，总称为一层低维linear bottleneck，其作用是将输入映射回低维空间

Inverted residuals

由上面的分析，直觉上我们认为linear bottleneck中包含了所有的必要信息，对于Expansion layer(即linear到深度卷积部分)仅是伴随张量非线性变换的部分实现细节，我们可将shortcuts放在linear bottleneck之间连接。示意图如下：

选择这样的结构，可以提升梯度在乘积层之间的传播能力，有着更好的内存使用效率。

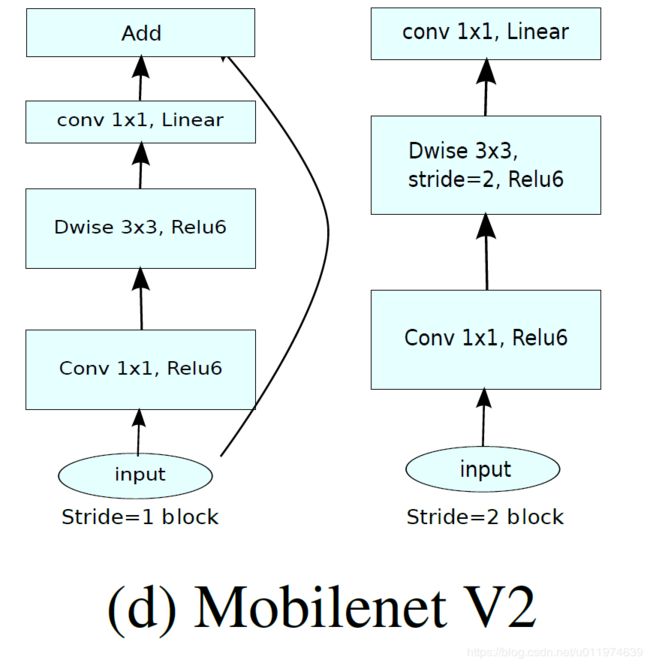
下表是bottleneck convolution的基本实现：

• 首先是1×1 conv2d变换通道，后接ReLU6激活(ReLU6即最高输出为6，超过了会clip下来)
• 中间是深度卷积,后接ReLU
• 最后的1×1 conv2d后面不接ReLU了，而是论文提出的linear bottleneck

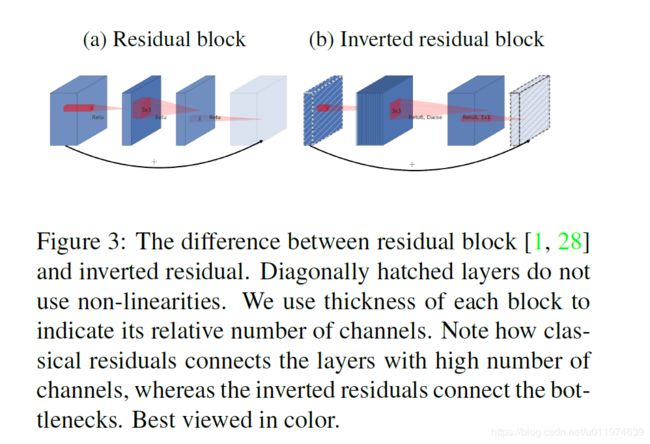
Inverted residuals结构示意图如下(方块的高度即代表通道数)：

可以看到相比与之前的残差模块，中间的深度卷积较宽，除了开始的升维的$1\times 1$卷积，做shortcut的$1\times 1$卷积通道数较少，呈现的是倒立状态，故称为Inverted residuals。

这样的结构在构建block时，自然的将输入和输出分离了。把模型的网络**expressivity (expansion layers，由扩展层决定)和capacity(encoded by bottleneck inputs，由bottleneck通道决定)**分开。

---

Model Architecture

构建的MobileNetv2的基本单元是bottleneck depth-separable convolution,下表给出了MobileNetv2的结构体系($28^2\times 32(s=2)\to 28^2\times 64(s=1)\to 14^2\times 96$这里步长设置应该反了)：

其中初始的全卷积为32个卷积核，后面接了19个 residual bottleneck layers。这里使用ReLU6(即$f(x)=min\{max(0,x),6\}$)作为非线性激活函数，这样在低精度计算下具有更强的鲁棒性。对于我们所有的实验，选择扩展因子(expansion factor)等于6，例如采用64的通道的输入张量产生128通道的输出，则中间的深度卷积的通道数为$6\times 64=384$。

Memory efficient inference

这部分没看懂，简单的翻译了一下

MobileNetv2中的inverted residual bottleneck对于移动设备有非常高效的实现。

对于整个模型计算图$G$，是由表示边的操作运算和表示节点的中间计算张量。 中间计算需要最小化存储在内存中的张量总数。多数情况下，这需要搜索所有合理计算顺序$\sum (G)$选择最小的：$$M(G)=\underset{\pi \in \sum (G)}{\min }\underset{i\in 1..n}{\max }\left[\sum _{A\in R(i,\pi ,G)}|A|\right]+size({\pi }_i)$$ 其中$R(i,\pi ,G)$是包含已连接${\pi }_i..{\pi }_n$任意节点的中间张量列表；$|A|$表示张量$A$的大小；$size(i)$是操作$i$期间所需的存储总和。

对于只有常见平行结构的图(例如残差结构)来说,只有一个非常见计算顺序可以简化计算图$G$上推断所需的内存：$$M(G)=\underset{op\in G}{\max }\left[\sum _{A\in o{p}_{inp}}|A|+\sum _{A\in o{p}_{out}}|B|+|op|\right]$$ 注意所需内存可简化为最大化计算所有操作的输入和输出组合的总大小,如果我们将bottleneck残差结构作为一个单一操作处理(即将内部卷积认为一次性张量)，那么总的内存量是由bottleneck张量主导的，而不是bottleneck内部的张量大小决定的(占比更大)。

对于Bottleneck Residual Block：

一个bottleneck block操作运算$F(x)$可表示为三个运算操作的组合$$F(x)=\left[A\cdot N\cdot B\right]x$$
其中

• $A:R^{s\times s\times k}\to R^{s\times s\times n}$是线性变换；
• $N:R^{s\times s\times n}\to R^{s^{\prime }\times s^{\prime }\times n}$是每个通道的非线性变换;
• $B:R^{s^{\prime }\times s^{\prime }\times n}\to R^{s^{\prime }\times s^{\prime }\times k^{\prime }}$是另一个输出的线性变换

对于MobileNetv2来说，$N=ReLU6\cdot dwise\cdot ReLU6$,但是结果适用于每个通道变换。假设输入大小主要由$|x|$主导，输出主要由$|y|$主导，那么$F(x)$计算所需的内存可以下降到$$|s^{2}k|+|s^{{}^{\prime }2}2k^{\prime }|+O(\max (s^2,s^{{}^{\prime }2}))$$

---

Experiment

训练细节：

部分	设置
使用工具	TensorFlow
训练器	RMSPropOptimizer, decay and momentum都设置0.9
标准的权重衰减	4e-5
学习率	初始学习率为0.045,每个epoch后衰减0.98
batch_size	16GPU内设置96
其他细节	每层后使用BN层

Ablation study

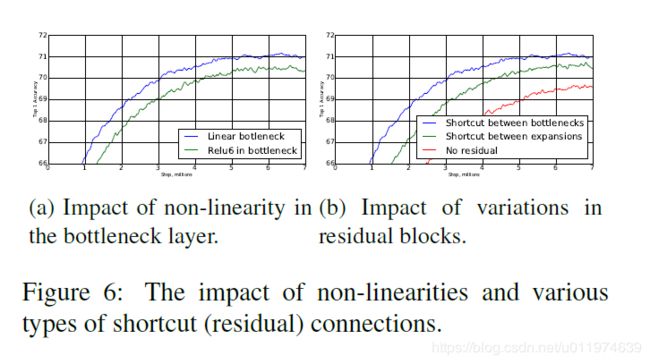
对于Inverted residual connections，验证不同结构下的连接方式对模型性能影响。对比结果如下图(b)所示：

图(a)是对比Linear Bottleneck设计的有效性：
从理论上来讲，linear bottleneck的限制不如non-linearities严重，因为linear bottleneck总能在线性范围改变偏置和缩放。图示liear bottleneck的效果要更佳，这为non-linearity操作在低维空间收益不佳的假设做了有力的验证。

ImageNet Classification

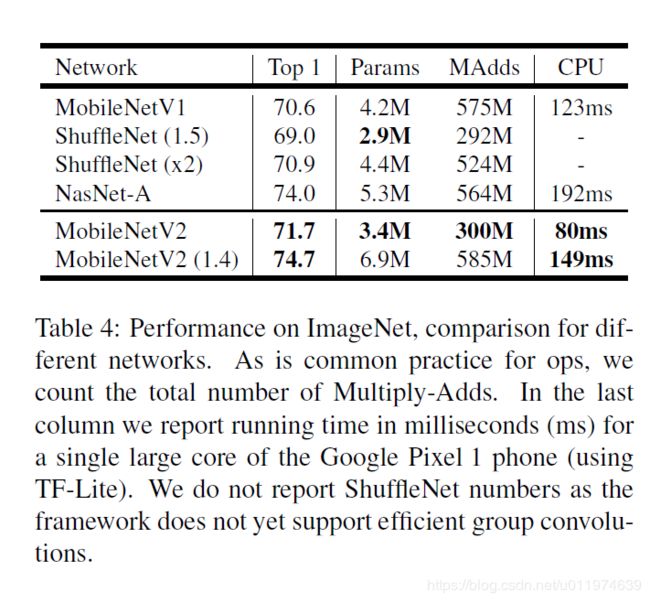
本次比较MobileNetv1，ShuffleNet和NASNet-A模型：

核心单元结构如下：

性能和参数对比如下：

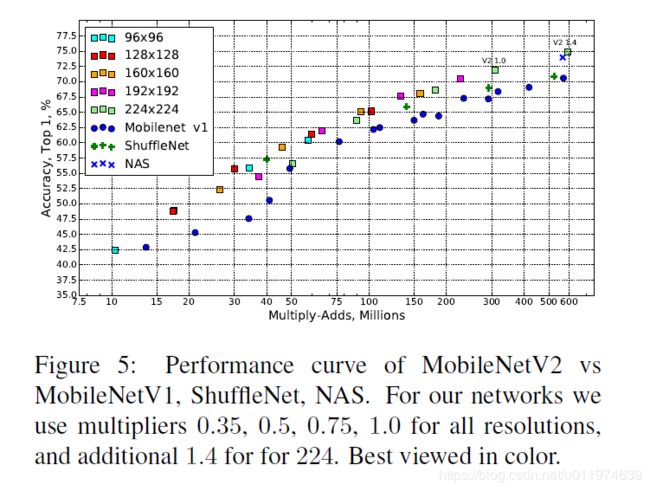
详细的对比图如下：

Object Detection

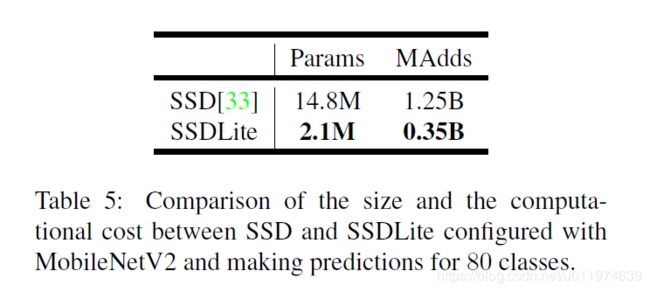
**SSDLite：**我们对SSD结构做了修改，将SSD的预测层中所有普通卷积替换为深度分离卷积，这样计算更高效，参数量和计算成本大大降低。如下图：

再对比评估了MobileNetv1和MobileNetv2的性能，还有YOLOv2和SSD网络在COCO数据集上表现，对于MobileNetv2来讲，SSDLite的第一层附加到第15层上作为扩展(官方代码没放出来，不确定这里具体怎么处理~)，第二层和SSDLite的其余部分附加到最后一层。对比如下：

MobileNetv2在极少的参数量下有着不错的性能~

Semantic Segmentation

将MobileNetv1，MobileNetv2以DeepLabv3为特征提取器做比较，在PASCAL VOC 2012上做比较。

在构建移动模型时，尝试了以下三种设计结构：

• 不同的特征提取器
  • 基于MobileNet系列的，和基于ResNet101系列的
• 简化DeepLabv3结构，加快计算
  • 对于DeepLabv3顶端部分(即ASPP模块)做处理
• 使用不一同的推理策略，提升性能
  • 使用数据增强，水平翻转、多尺度输入等

对比结果如下：

从表中总结一下：

• 使用包括MF(多尺度和随机翻转)配置的推理策略显著增加计算量(MAdds)，不适合应用在移动设备上。
• 使用输出OS(输出步幅)=16的比OS=8的要有效
• MobileNetv1相比ResNet已经是强大的特征提取器了
• DeepLabv3的顶端部分在MobileNetv2倒数第二个特征映射上构建比在最后的特征映射上构建要有效，倒数第二层的通道数为320，而最后一个为1280，这样能显著减少计算量，而在性能上只是略微的受损
• DeepLabv3的顶端部分计算成本很高，移除ASPP模块可显著的减少MAdds，却只有少量的性能损失(黑体加粗部分，有较好的性能，计量下降到只有2.75B)

---

Conclusion

论文设计的新的Inverted residual bottleneck结构，能够构建一系列高效移动模型，基本的构建单元具有多种特性，同时在内存处理上有极好的性质。新提出的Inverted residual bottleneck结构在理论上具有独特的性质，允许将网络expressivity (expansion layers，由扩展层决定)和capacity(encoded by bottleneck inputs，由bottleneck通道决定)分开，这是未来研究的重要方向。

---

附录

本文非常好在有许多数学上的证明，不再是结果（很多文章都是State-of-the-art，所以我的模型就是好，上一篇有这种感觉的文章是ResNet_{）说明一切的，而是有理论指导的了}

但是我没怎么看懂，等有时间的好好琢磨一下~

---