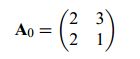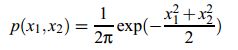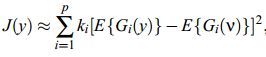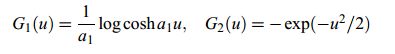尝试理解ICA（Independent Component Analysis）独立成分分析

1.从鸡尾酒会问题（cocktail party problem）说起

ICA最早是从神经网络领域开始研究的，应用于信号分离、特征提取。为了简单，我们这里从一个经典的例子开始——盲源信号分离（blind signal separation）。

假设在一个开party的房间里有两个人同时说话，房间里两个不同的位置上各放一个麦克风，记录了两段声音（时间信号），x1(t)和x2(t)，这两段声音都记录了两个人说的话，我们怎样得到他们分别说了什么话呢？

记源信号是s1(t)和s2(t)，这个问题可以用以下等式描述：

四个参数aij与说话者跟麦克风的距离有关。

示意图如下：

接收到的信号x1,x2:

需要我们去还原的信号s1,s2：

研究表明，如果s1,s2是统计独立的随机信号，那么就可以用x1,x2去还原。ICA正是利用统计上的独立性从混合信号中分解出源信号的。

2.ICA模型介绍

2.1定义ICA

这里我们用隐含变量（latent variables）模型来描述ICA：

假设有n个观测信号x1,...,xn，来自n个独立成分的混合s1,...,sn 。其中A是nxn的混合矩阵（mixing matrix）。

模型假设如下：

1.si之间是统计独立的；

2.si服从非高斯分布；

3.混合矩阵是方阵（可以放松），且可逆。

那么，，W是A的逆。

独立成分是隐含变量，也就是说他们不能被直接观测到。A和s都是未知的。

2.2ICA的不确定性

1.不能确定独立成分的方差或者说能量

因为A和s都是未知的，s缩放的倍数可以在A上补偿回来：。

因此我们统一假设各独立分量的方差为1，。其实，这样假设之后仍然存在一个不确定性，独立分量乘以-1并不影响方差。不过在实际应用时，并不影响。

2.不能确定各独立分量的顺序

同样，由于A和s都是未知的，在预测时我们可以任意改变A和s对应分量的位置，在矩阵运算中就是乘以一个置换矩阵：。

2.3举个例子

假设独立成分s1,s2服从以下均匀分布：

可以证明出这个均匀分布的均值为0，方差为1。

联合概率密度的分布是这样的，横轴是s1,纵轴是s2：

混合矩阵如下：

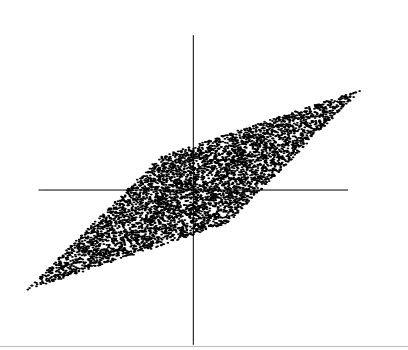
使得x1,x2在如下的平行四边形上符合均匀分布，横轴是x1,纵轴是x2：

我们要做的就是通过x1,x2预测混合矩阵。可以这样预测A：先估算x1,x2的联合概率密度，然后找到边缘，平行四边形的边缘在A的列所在的方向上。不过这只适用于均匀分布。实际上独立成分可以是任意非高斯分布，我们要去找一个通用的方法。

3.独立性的说明

3.1独立

若随机变量y1,y2独立，则而且有性质：

可以理解为yi的取值对yj的取值没有提供信息。

证明如下：

3.2不相关

若随机变量y1,y2不相关，则。不相关是独立的一种较弱的表现形式，独立一定不相关，不相关不一定独立。许多ICA方法用不相关来估计独立成分，以达到减少参数和简化问题的目的。

3.3高斯的不相关和独立是等价的

假设混合矩阵是方阵，如果s1和s2都是服从高斯分布，那么x1,x2也是高斯的，且不相关，方差为1 。联合概率密度如下：

从图中可以看出，分布是对称的，这样就失去了方向信息，也就是A的列向量的信息。A也就预测不出来了。可以证明，一个高斯分布经过正交变换以后仍然是那个高斯分布，而且变量之间仍是独立的，所以如果变量都是高斯分布的，我们只能知道A是一个正交变换，不能完全确定A。但是，如果只有一个变量服从高斯分布，仍然是可以用ICA解混的。

4.ICA估计的原理

4.1非高斯分布是估计的关键

上面已经分析，高斯分布不能用ICA估计。

中心极限定理告诉我们，多个独立的自由变量的和近似服从高斯分布。这是ICA估计的重要依据。回到上面的例子中，两个独立自由变量的和比它们任意一个都要接近高斯分布。

我们用下式来估计独立分量：如果w是A的逆的一列，那么y就是一个独立分量。现在，我们要用中心极限定理估计出w。

先做一下变量的转换，令，则。这样y就变成si的线性组合，zTs 比任一个si都要接近高斯除非它就等于其中一个si，此时，z只有一个分量是非0的。因此，我们可以找一个向量w，使得的非高斯性最大，而这个w对应于一个z，这个z只有一个非0分量，即=其中一个独立分量。

实际上，在n维空间里最优化非高斯性会得到2n个极值，每一个独立分量对应两个极值，si和-si。w是把x转换到另外一个空间，在这个空间里，x的各个列是不相关的（以此代表不独立）。可以通过正交变换找到这些极值。

4.2非高斯性的度量

1.峰度/峭度（Kurtosis）

或者说随机变量的四阶累积量（fourth-order cumulant），定义为：

既然我们已经假定y的方差是1，E{y2} =1，那么峰度可以简化为随机变量的四阶矩：。

高斯函数的峰度=0，对于大部分随机变量而言峰度都是非零的。

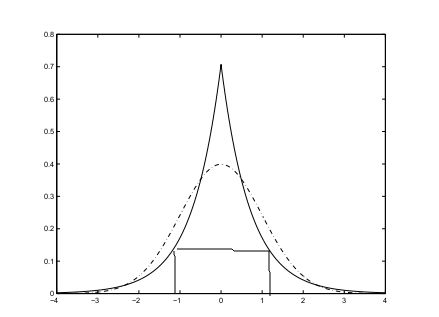
如果随机变量的分布是次高斯的（subgaussian）或者说是平峰的（platykurtic），峰度为负；超高斯的（supergaussian）或者说是尖峰的（leptokurtic），峰度为正。

比如说，拉普拉斯分布就是尖峰的，均匀分布则是平峰的。

有时也用峰度的平方或者绝对值去度量非高斯性，这样峰度值就非负了。

峰度有两个重要性质：

找到峰度的最值也就找到独立分量了。以二维为例，独立分量是令

依然，我们假设s1,s2的方差为1，那么就有约束：问题就转化为求在单位圆上的极值。

可以证明，当z的一个分量为非零，另一个分量为零时取得极值。这里由于单位圆的限制，非0元素只能是1或-1。实际中，会从一些w开始，找到y的峰度变化最快的方向，然后用梯度下降的方法更新w，直到找到所有极值。

峰度的缺点：

峰度对异常值（outliers）很敏感，它的值主要取决于处于分布的尾巴处的观测值。因此用峰度度量非高斯性，鲁棒性不好。

2.负熵（Negentropy）

负熵来自于信息论中熵的概念。在编码时，熵和编码的长度有着密切的联系。

离散自由变量Y的熵定义为：

连续自由变量Y的熵定义为（f(y)是概率密度）：

信息论中已经证明：方差相同时，服从高斯分布的随机变量熵最大。这说明高斯分布是the “most random” or the least structured of all distributions。如果变量的分布集中或者说概率密度函数比较尖，那么它的熵就很小。刚好，我们可以用它来度量分布的非高斯性。

定义负熵如下：

是一个与y具有相同的协方差矩阵的高斯变量。负熵总是非负的，当y是高斯分布时为0。随机变量经过可逆的线性变换，负熵不变。可以证明，负熵是非高斯性的最优度量。

负熵的缺点：

计算太复杂，需要计算积分。

负熵的近似：

1.高阶矩近似

y假定是零均值单位方差的。这个近似带来了峰度很差的鲁棒性。

2.最大熵原理近似

ki是大于0 的常数，v是一个零均值单位方差的高斯变量，y假定是零均值单位方差的，Gi是非二次的函数。近似虽然不精确，但是总是非负，当y是高斯分布时为0。

如果只用一个非二次函数，则变成了：

变成了高阶矩近似的泛化，当时，就与近似1效果一致，但鲁棒性更好。

一种被证明好用的G：

4.3.互信息量（Mutual Information）

由信息论发展来的ICA估计的方法，最终也是寻找最大的非高斯性所在的方向。

互信息量定义：

互信息量描述变量之间的独立性，非负，当变量两两独立的时候为0。所以互信息量反映的是真正的独立性了，而不仅仅是不相关。互信息量为0 表明一个变量已知不带给另一个变量任何信息。

对于可逆的线性变换，自由变量yi的互信息量与x的信息量有如下关系：

我们已经假设yi之间是不相关的而且方差为1，则进一步有：

中间那一项是固定的了，那么detW也必须是一个固定值。这样负熵和互信息量之间只相差一个常数，这个参数与变量有关，与W无关：

最小化互信息量就相当于寻找最大化负熵所在的方向，也相当于寻找在所有负熵的极值所在的子空间中有最大投影的子空间，也就是使各估计值的非高斯性的和最大。

这样我们也可以最小化互信息量来求解W。

4.4用最大似然法做估计

可逆线性变换，y的概率密度由下式给出：。

假设si的概率密度是fi，x(t)，t=1,...,T,是x的观测值,那么W的对数似然估计如下：

对W求导，更新w直到求得L的最大值。直观解释就是求W，使观测值出现的概率最大。

对上式求期望可以得到：

如果fi等于的真实分布，那么上式第一项等于，这样似然估计和互信息量取负号相差一个常数值。所以似然估计和互信息量是等价的。

实际应用时，我们并不知道si的概率密度分布是什麽，只能用的最大似然估计去近似si的概率密度，这样最大似然估计反而更好用。

5.ICA的预处理

5.1中心化（Centering）

就是将数据零均值化。

5.2白化（Whitening）

就是将数据经过线性变换去相关，并使各变量的方差为1.即：

可以通过将数据的协方差矩阵进行特征值分解（eigen-value decomposition ，EVD）得到：

，D=diag(d1,...,dn)

白化后的

，

进一步，

 白化减少了A要估计的参数，由n^2变为了n(-1) / 2。而且在这个时候我们可以将数据进行降维（PCA）。

6.FastICA
待更新

利用负熵的一个matlab程序：

（效果一般）

samplerate=500; % in Hz
N=500; % data length

freq1=10; % in Hz
freq2=5; % in Hz
taxis=[1:N]/samplerate;

% generate test signals 
C1 = 0.5*sin(2*pi*freq1*taxis);        
C2 = sawtooth(2*pi*freq2*taxis,1);    
figure, 
subplot(2,1,1)
plot(taxis,C1)
subplot(2,1,2)
plot(taxis,C2)

% Combine data in different proportions
X(1,:) = 0.9*C1 + 0.3*C2 + 0.1*rand(1,N);
X(2,:) = 0.4*C1 + 0.7*C2 + 0.1*rand(1,N);

figure, 
for i=1:size(X,1)
    subplot(size(X,1),1,i)
    plot(taxis,X(i,:))
end
 
%以下程序调用ICA，输入观察信号，输出为解混合信号
% 这是对信号源进行负熵分离
%---------预白化处理----------
[m,n]=size(X);  %m是信号个数，n是采样点数
zerox=X-mean(X,2)*ones(1,n);%中心化
Cxx=cov(zerox');
[vector,value]=eig(Cxx);
value=abs(value);
whiteMatrix=value^(-1/2)*vector';%白化处理
Z=whiteMatrix*zerox;

% --------使用负熵分离信源----------
maxcount=100;%设定最大的循环次数
minvalue=1E-6;%设定收敛的门限值
w=ones(m,m);%设定初始的权矢量
B=[];
for k=1:m
    wp=w(:,k);
    count=0;
    lastwp=zeros(m,1);
    while abs(abs(wp'*lastwp)-1)>minvalue
        count=count+1;
        lastwp=wp;
        for i=1:m     
       %选择的G函数是G(y)=-exp(-y^2/2)
            g=(lastwp'*Z).*exp(-0.5*(lastwp'*Z).^2);%一阶微分
            dg=(1-(lastwp'*Z).^2).*exp(-0.5*(lastwp'*Z).^2);%二阶微分
%---------------更新-------------------------
            wp(i,:)=mean(Z(i,:).*g)-mean(dg)*lastwp(i,:);
         end
%---------对已经提取的分量进行正交化-----------------
        if(k>1)
            wp=wp-w(:,1:(k-1))*w(:,1:(k-1))'*wp;
        end
         wp=wp./norm(wp);  %归一化  norm是求矩阵的2-范数
        if count>=maxcount
           fprintf('未找到相应的信号');
           return;
       end
    end
     w(:,k)=wp;
end
Z=w'*Z;

figure,
for i=1:size(Z,1)
    subplot(size(Z,1),1,i),plot(Z(i,:))
end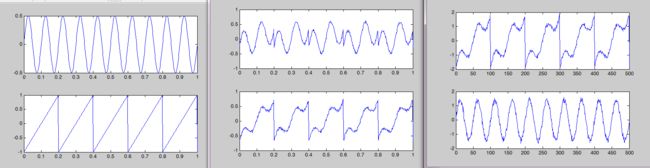

7.ICA和PCA的区别

PCA主要用于数据的降维，将原本相关的数据映射到一个新的空间中，在这个空间中，数据的各个维度是不相关的；ICA是一种找到数据可能存在的各组成分量的方法，主要应用于信号解混，特征提取，使用ICA时往往对数据存在几点假设：源信号独立，且服从非高斯分布，甚至要假设源信号的概率分布和个数。ICA使得WTx的非高斯性最大，找到独立分量。PCV往往是ICA预处理的一部分。

可参见知乎回答： https://www.zhihu.com/question/28845451/answer/42292804