反向传播算法

原文链接： https://www.jiqizhixin.com/graph/technologies/7332347c-8073-4783-bfc1-1698a6257db

反向传播（英语：Backpropagation，缩写为BP）是“误差反向传播”的简称，是一种与最优化方法（如梯度下降法）结合使用的，用来训练人工神经网络的常见方法。该方法计算对网络中所有权重计算损失函数的梯度。这个梯度会反馈给最优化方法，用来更新权值以最小化损失函数。 在神经网络上执行梯度下降法的主要算法。该算法会先按前向传播方式计算（并缓存）每个节点的输出值，然后再按反向传播遍历图的方式计算损失函数值相对于每个参数的偏导数。

来源：维基百科Google ML glossary

简介

BP算法是“误差反向传播”的简称，是一种与最优化方法（如梯度下降法）结合使用的，用来训练人工神经网络的常见方法。该方法对网络中所有权重计算损失函数的梯度。这个梯度会反馈给最优化方法，用来更新权值以最小化损失函数。

反向传播要求有对每个输入值期望得到的已知输出，来计算损失函数的梯度。因此，它通常被认为是一种监督式学习方法，虽然它也用在一些无监督网络（如自动编码器）中。它是多层前馈网络的Delta规则的推广，可以用链式法则对每层迭代计算梯度。反向传播要求人工神经元（或“节点”）的激励函数可微。

算法简介

BP网络的结构降法的基础上。BP网络的输入输出关系实质上是一种映射关系：一个 输入m输出的BP神经网络所完成的功能是从 一维欧氏空间向m维欧氏空间中一有限域的连续映射，这一映射具有高度非线性。它的信息处理能力来源于简单非线性函数的多次复合，因此具有很强的函数复现能力。这是BP算法得以应用的基础。

反向传播算法主要由两个环节(激励传播、权重更新)反复循环迭代，直到网络的对输入的响应达到预定的目标范围为止。

BP算法的学习过程由正向传播过程和反向传播过程组成。在正向传播过程中，输入信息通过输入层经隐含层，逐层处理并传向输出层。如果在输出层得不到期望的输出值，则取输出与期望的误差的平方和作为目标函数，转入反向传播，逐层求出目标函数对各神经元权值的偏导数，构成目标函数对权值向量的梯量，作为修改权值的依据，网络的学习在权值修改过程中完成。误差达到所期望值时，网络学习结束。

激励传播

每次迭代中的传播环节包含两步：

1. (前向传播阶段)将训练输入送入网络以获得激励响应；
2. (反向传播阶段)将激励响应同训练输入对应的目标输出求差，从而获得隐层和输出层的响应误差。

权重更新

对于每个突触上的权重，按照以下步骤进行更新：

1. 将输入激励和响应误差相乘，从而获得权重的梯度；
2. 将这个梯度乘上一个比例并取反后加到权重上。
3. 这个比例将会影响到训练过程的速度和效果，因此称为“学习率”或“步长”。梯度的方向指明了误差扩大的方向，因此在更新权重的时候需要对其取反，从而减小权重引起的误差。

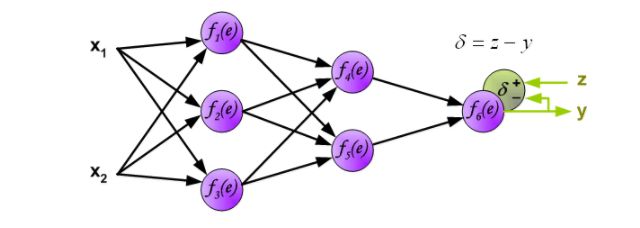
项目描述多层神经网络采用反向传播算法。为了说明这一过程,这里有三层神经网络，有两个输入和一个输出,如下图中所示,

每个神经元是由两个单元组成的。第一个方块包含权重系数和输入信号。第二个方块实现非线性函数,称为神经元激活函数。

e是上一层summing junction的输出信号，y = f(e)是非线性元件的输出信号。信号y也是神经元的输出信号。

我们需要的神经网络训练数据集。训练数据集由输入信号(x_1和x_2)分配相应的目标(预期的输出)为z。网络训练是一个迭代的过程。在每个迭代中权重系数的节点会用新的训练数据集的数据进行修改。修改计算使用下面描述的算法:每个步骤都是从训练集中的两个输入信号开始,在这个阶段我们可以确定每个网络层中的每个神经元的输出信号值。图片下面的说明信号是通过网络传播,符号w(x_m)_n代表网络输入x_m和神经元n层之间的连接权重，符号y_n代表神经元n的输出信号。

传播的信号需要通过隐藏层。符号w_mn代表m和输入和输出神经元n之间的连接权重。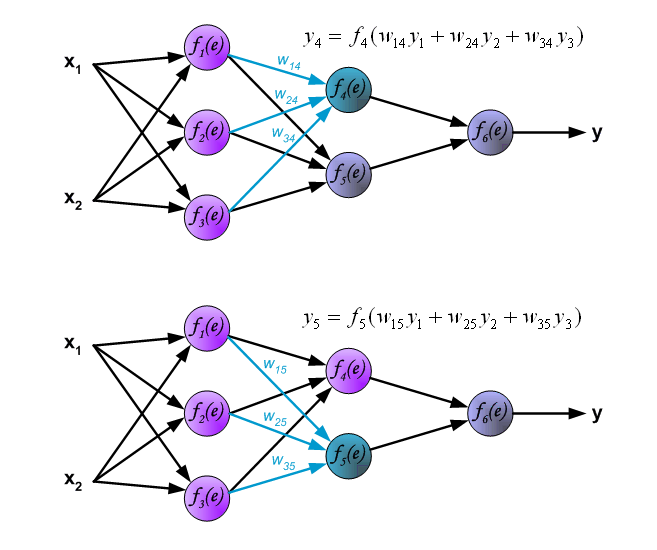

传播信号通过输出层。

以上都是正向传播。算法的下一步，计算得出的输出y和训练集和的真实结果z有一定的误差，这个误差就叫做误差信号。用误差信号反向传递给前面的各层，来调整网络参数。

之前的算法是不可能直接为内部神经元计算误差信号,因为这些神经元的输出值是未知的。因此反向传播算法对此问题进行了解决。这个算法的创新点就是传播误差信号δ=z-y，返回到所有神经元,输出信号会根据输入神经元进行更改。

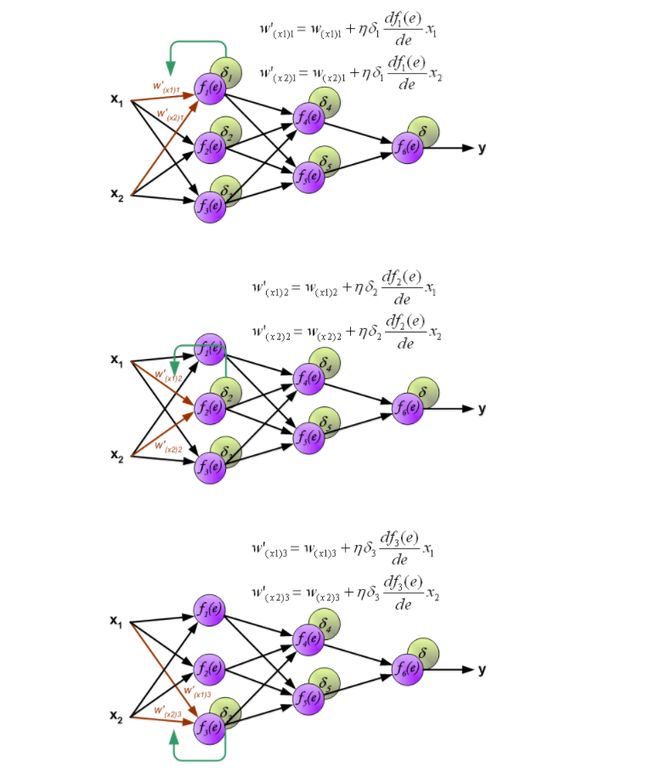
权重系数的W_mn用来传播误差信号δ，它是等于通过计算得出输出值，便会得到新的误差δ_m。只有数据流的方向是改变(信号传播从输出到输入一个接一个的进行权值更新)。这一技术是用于所有网络层。如果当传播错误来自一些神经元。将误差δ根据之前的权重会获得每个神经元的各自误差δ_5，δ_4，...δ_1.

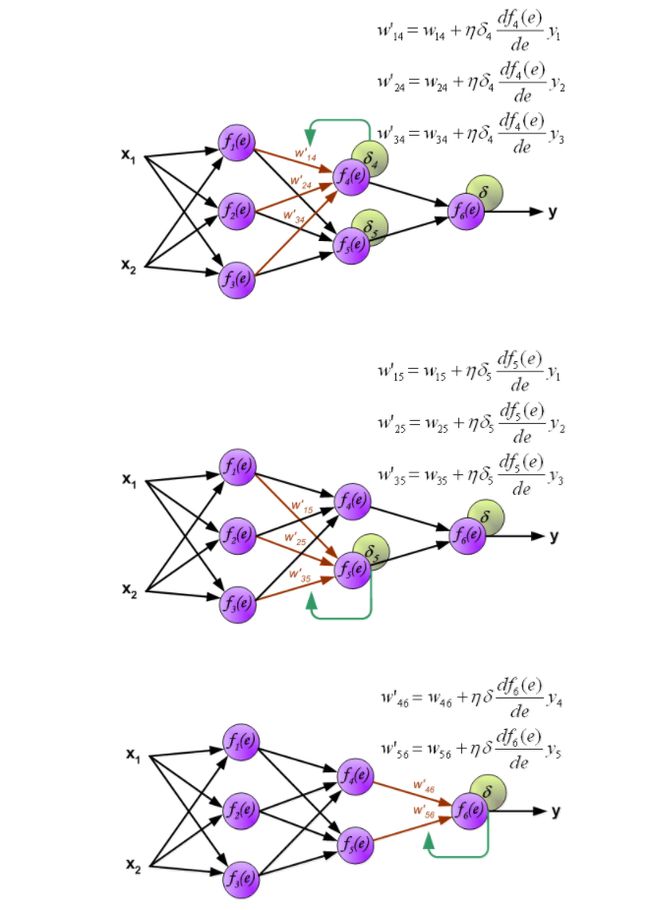
当每个神经元的误差都计算完后，每个神经元的权重系数也会更新。下面的公式就是神经元的激活函数（更新权重），利用误差δ_1和之前的权重以及之前e函数的倒数来获得新的权重w'.这里η是系数，它影响着权重改变大小的范围。它的选择也是有很多方法的。

以上就是正向传入输入值，获得误差，根据误差反向传播误差，获得每一个神经元的误差值，在根据误差值和e的倒数来更新权重，达到了对整个网络的修正。

【出处：Principles of training multi-layer neural network using backpropagation ，URL：http://www.cs.unibo.it/~roffilli/pub/Backpropagation.pdf】

发展历史

根据各种资料，反向传播是由1960年代Henry J. Kelley提出的控制理论control theory和 1961年Arthur E. Bryson 提出的理论衍生而来的。他们的使用的思想是动态规划。在1962年， Stuart Dreyfus 出版了一个更加简单的衍生版本链式规则chain rule。Bryson 和 Ho 在1969年形容这个为multi-stage的动态系统优化方法。1969年,作为人工神经网络创始人的明斯基(Marrin M insky)和佩珀特(Seymour Papert)合作出版了《感知器》一书,论证了简单的线性感知器功能有限,不能解决如“异或”(XOR )这样的基本问题,而且对多层网络也持悲观态度。这些论点给神经网络研究以沉重的打击,很多科学家纷纷离开这一领域,神经网络的研究走向长达10年的低潮时期。

在1970， Linnainmaa 出版了一个为了解决discrete connected networks的自动分化问题更加通用的方法。这就是所对应的backpropagation，它即使实在稀疏网络也非常有效率。

1974年哈佛大学的Paul Werbos发明BP算法时，正值神经外网络低潮期，并未受到应有的重视。1 Werbos提到了将此应用于ANN的可能性，Harvard博士生Paul Werbos首次提出了backprop. 并且在1982年，他将Linnainmaa's AD方法应用于神经网络中，这就是现在的适用方式。但是当时并没有收到太多的关注。

1983年，加州理工学院的物理学家John Hopfield利用神经网络，在旅行商这个NP完全问题的求解上获得当时最好成绩，引起了轰动。然而,Hopfield的研究成果仍未能指出明斯基等人论点的错误所在,要推动神经网络研究的全面开展必须直接解除对感知器——多层网络算法的疑虑。

在1986年，Rumelhart, Hinton 和 Williams展示了这个方法可以根据输入数据适用隐含层来表示内在的联系。在1993年，Wan第一次适用反向传播赢得了国际模式识别竞赛。

在2000s，神经网络并没有太过火热，反而到了2010s，BP神经网络风靡了很多研究领域，这也是得益于基于便宜，强大的GPU的运算系统。

【出处：wiki ，URL：https://en.wikipedia.org/wiki/Backpropagation】

主要事件

年份	事件	相关论文/Reference
1974	Werbos, P.发明BP算法	Werbos, P. (1974). Beyond regression: new fools for prediction and analysis in the behavioral sciences. PhD thesis, Harvard University .
1986	Rumelhart, Hinton 和 Williams展示了这个方法可以根据输入数据适用隐含层来表示内在的联系。	Rumelhart, D. E., Hinton, G. E., & Williams, R. J. (1986). Learning representations by back-propagating errors. nature, 323(6088), 533.
1995	Cortes, C.,提出SVM	Cortes, C., & Vapnik, V. (1995). Support-vector networks. Machine learning, 20(3), 273-297.
1998	LeCun等人提出LeNet	LeCun, Y., Bottou, L., Bengio, Y., & Haffner, P. (1998). Gradient-based learning applied to document recognition. Proceedings of the IEEE, 86(11), 2278-2324.
2012	ALEX等人提出ALEXNET	Krizhevsky, A., Sutskever, I., & Hinton, G. E. (2012). Imagenet classification with deep convolutional neural networks. In Advances in neural information processing systems (pp. 1097-1105).

发展分析

瓶颈

BP神经网络无论在网络理论还是在性能方面已比较成熟。其突出优点就是具有很强的非线性映射能力和柔性的网络结构。网络的中间层数、各层的神经元个数可根据具体情况任意设定，并且随着结构的差异其性能也有所不同。但是BP神经网络也存在以下的一些主要缺陷。

• 学习速度慢，即使是一个简单的问题，一般也需要几百次甚至上千次的学习才能收敛。
• 容易陷入局部极小值。
• 网络层数、神经元个数的选择没有相应的理论指导。
• 网络推广能力有限。
• 可解释性瓶颈，对网络输出结果不具备可靠的数学可解释性
• 神经网络对推理，规划等人工智能领域的其他问题还没有特别有效的办法。另外由于其参数数量巨大，对高计算性能硬件的依赖大，难以部署在轻量级低功耗硬件上，如嵌入式设备等
• 反向传播算法缺乏仿生学方面的理论依据，显然生物神经网络中并不存在反向传播这样的数学算法

未来发展方向

BP网络主要用于以下四个方面。

1)函数逼近：用输入向量和相应的输出向量训练一个网络逼近一个函数。

2)模式识别：用一个待定的输出向量将它与输入向量联系起来。

3)分类：把输入向量所定义的合适方式进行分类。

4)数据压缩：减少输出向量维数以便于传输或存储。

除此之外，在神经网络的可解释性研究方面，向低功耗硬件迁移，以及在认知计算，规划推理等方面和其他传统技术进行结合探索

Contributor：Ruiying Cai