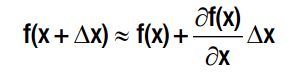上回说到从场景中提取特征点,并且对不同角度中的特征点进行匹配。这次要先介绍一个工具 —— 拟合。拟合本质上是一个优化问题,对于优化问题,最基本的是线性最小二乘法。换言之,我们需要保证拟合误差最小。
1、最小二乘法拟合
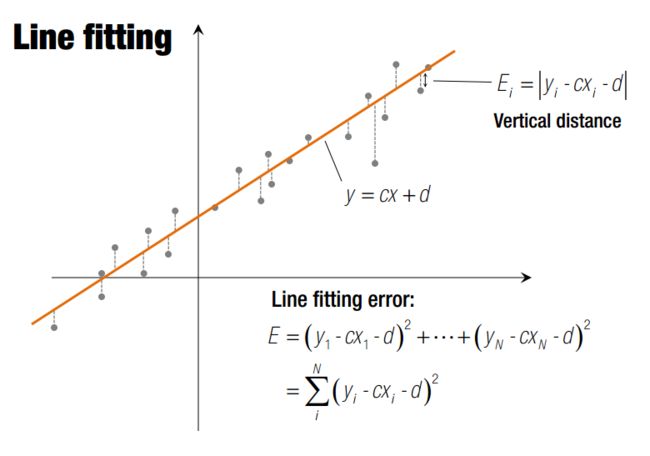
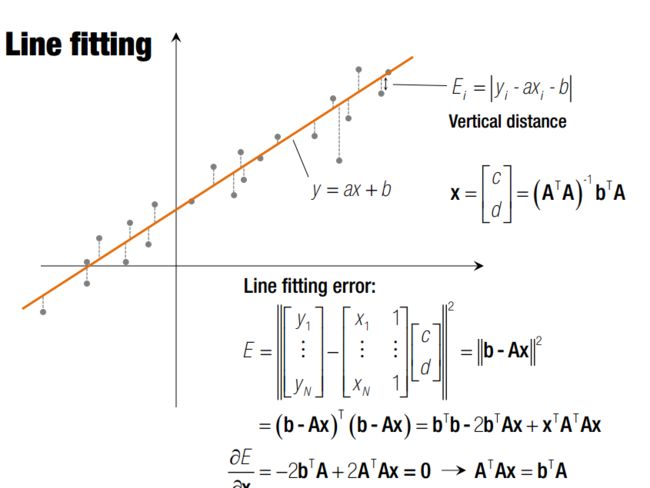
基本的最小二乘法拟合解决的是 点 --- 模型 的拟合问题。以点到直线的拟合为例,按照拟合误差的建模,该问题可以分为两类。
第一类以 因变量 误差作为优化目标,该类问题往往是自变量---因变量模式,xy的单位不同。
第二类以 距离 作为优化目标,该类问题xy的单位往往相同,直线不代表趋势,而是一种几何模型。
由于优化目标不同,故建模方式与解均不同,但是解法思路是一样的,都是讲求和化作向量的模。而向量又是矩阵的运算结果,最终化为奇异值分解问题。
2、RASAC拟合
此问题之前已经详细论述过,见博客
3、非线性拟合
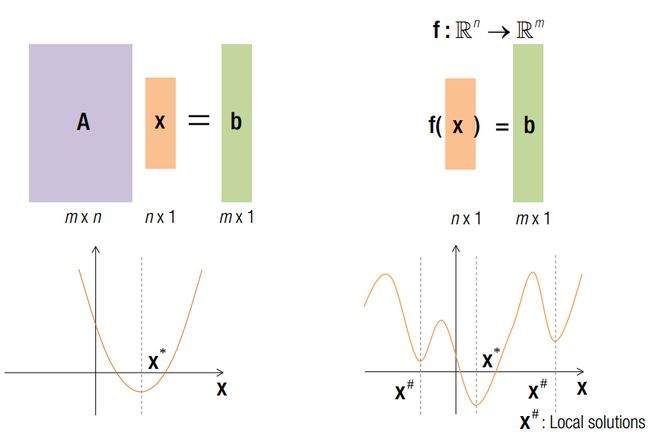
线性最小二乘法已经有了很好的解释。但是生活总是如此不易。。。能化成上述标准矩阵形式的问题毕竟还是少数,大部分情况下,我们面对的不是min(||Ax - b||),而是 min(||f(x)-b||) !!!
在三维重建中,如果我们有2个以上视角,那么三条线很可能是不交于一点的。原因是我们选择的旋转矩阵有精度表达问题,位姿估计也存在误差。使用奇异值分解的方法是求得到三条线距离最小的点,还有一种合适的估计,是使得该点在三个相机上的重复投影误差最小。同时,R,T,P(X,Y,Z)进行估计,最终保证Reprojection err 最小的方法————the state of the art BUNDLE ADJUST.
先回到最原始的问题,如何求解非线性最小二乘法。
由线性最小二乘法,我们可以得到非线性最小二乘法矩阵表达形式。如果要求得其局部最小值,则对 x 求导后,导数应为 0。
然而,这个东西并不好解,我们考虑使用梯度下降迭代的方式。这里使用的是单纯的梯度。
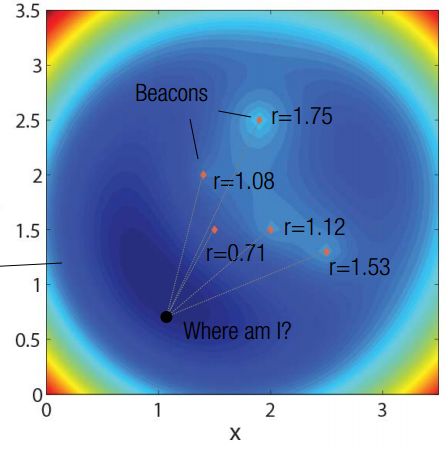
这里有个非常不好理解的地方,其假设detaX非常小,故表示成上述形式,以保证 f(x + deta_X) 以信标定位为例。讲道理,两个信标为圆心画圆应该给出位置的两个解析解。但是如果有很多信标,那么信标就会画出一块区域........这是SLAM里的经典问题了,后面会有博客专门讲BUNDLE ADJUST.