Machine Learning in Action(机器学习实战)之支持向量机(Support-Vector-Machines(SVM))算法学习笔记
1. 学习环境
windows10 、Anaconda(向初学者推荐这个工具) + Pycharm2018 、python 3.7。
2. Support Vector Machines概述
2.1 支持向量机优缺点
优点:泛化错误率低,计算开销不大,结果易解释。
缺点:对参数调节和核函数的选择敏感,原始分类器不加修改仅适用于处理二类问题。
适用数据类型:数值型和标称型数据。
2.2 支持向量机的一般流程
⑴收集数据:可以使用任意方法。
(2)准备数据:需要数值型数据。
(3)分析数据:有助于可视化分隔超平面。
(4)训练算法:SVM的大部分时间都源自训练,该过程主要实现两个参数的调优。
(5)测试算法:十分简单的计算过程就可以实现。
(6)使用算法:几乎所有分类问题都可以使用SVM,值得一提的是,SVM本身是一个二类分类器,对多类问题应用SVM需要对代码做一些修改。
3.应用简化版SMO算法处理小规模数据集
3.1 SMO 算法中的辅助函数
from numpy import *
#SMO 算法中的辅助函数
#loadDataSet()函数,该函数打开文件并对其进行逐行解析,
# 从而得到每行的类标签和整个数据矩阵。
def loadDataSet(fileName):
dataMat = []; labelMat = []
fr = open(fileName)
# readlines()方法:1、一次性读取整个文件。 2、自动将文件内容分析成一个行的列表。
for line in fr.readlines():
# strip()函数将文本中的每行最后一个换行符去掉
# plit('\t')把每行中的字符一个个按横向制表符(\t)拆分开,变成list
lineArr = line.strip().split('\t')
# list.append(obj) 在列表末尾添加新的对象
dataMat.append([float(lineArr[0]), float(lineArr[1])])
labelMat.append(float(lineArr[2]))
return dataMat, labelMat
#selectJrand()有两个参数值,其中1是第一个alpha的下标,m是所有alpha的数目。
# 只要函数值不等于输人值1,函数就会进行随机选择
def selectJrand(i, m):
j = i
while (j ==i):
# numpy 中random()函数
#random.uniform(x, y) 方法将随机生成下一个实数,它在 [x,y] 范围内。
j = int(random.uniform)
return j
#clipAlpha()它是用于调整大于H或小于L的alpha值
def clipAlpha(aj, H, L):
if aj > H:
aj = H
if L > aj:
aj = L
return aj
dataArr, labelArr =loadDataSet('testSet.txt')
print(labelArr)
测试结果:
3.2 简化版 SMO 算法
#简化版 SMO 算法
#该函数有5个输人参数,分别是:数据集、类别标签、常数C、容错率和退出前最大的循环次数
def smoSimple(dataMatIn, classLabels, C, toler, maxIter):
#调用mat()函数可以将数组转换为numpy矩阵,然后可以对矩阵进行一些线性代数的操作。
#简化很多数学操作
#transpose()函数的作用就是调换数组的行列值的索引值,类似于求矩阵的转置:
#转置了类别标签,因此我们得到的就是一个列向量而不是列表
#于是类别标签向量的每行元素都和数据矩阵中的行一一对应。
dataMatrix = mat(dataMatIn); labelMat = mat(classLabels).transpose()
#通过shape()函数得到数据集的行数和列数(m,n)
b = 0; m,n = shape(dataMatrix)
#zeros()函数构建一个alpha列矩阵(m 行 1 列),矩阵中元素都初始化为0
#调用mat()函数将矩阵转换为numpy矩阵,对矩阵进行一些线性代数的操作,简化很多数学操作
alphas = mat(zeros((m,1)))
#并建立一个让61变量。该变量存储的则是在没有任何alpha改变的情况下遍历数据集的次数。
# 当该变量达到输入值 maxIter 时,函数结束运行并退出。
iter = 0;
while (iter < maxIter):
#每次循环当中,将alphaPairsChanged先设为0,该变量用于记录 alpha 是否巳经进行优化
#在循环结束时就会得知这一点
alphaPairsChanged = 0
#对整个集合顺序遍历
for i in range(m):
#首先,fXi能够计算出来,这就是我们预测的类别
fXi = float(multiply(alphas, labelMat).T*(dataMatrix*dataMatrix[i, :].T)) + b
#然后,基于这个实例的预测结果和真实结果的比对,就可以计算误差Ei 。
# 如果误差很大,那么可以对该数据实例所对应的 alpha 值进行优化
Ei = fXi - float(labelMat[i])
#在if语句中,不管是正间隔还是负间隔都会被测试。并且在该if语句中,也要同时检查alpha值,
# 以保证其不能等于0或C。由于后面alpha值小于0或大于C将被调整为0或C所以一旦在该if语句中
# 它们等于这两个值的话,那么它们就已经在“边界”上了,因而不再能够减小或增大,
# 因此也就不值得再对它们进行优化了。
if((labelMat[i])*Ei < -toler) and (alphas[i] < C) or \
((labelMat[i]*Ei > toler) and \
(alphas[i] > 0)):
# 如果当前向量可以被优化,随机选择另外一个数据向量
#通过selectJrand()函数来随机选择第二个alpha值
j = selectJrand(i, m)
#可以采用第一个alpha值(alpha[i]) 的误差计算方法,来计算这alpha值的误差
fXj = float(multiply(alphas, labelMat).T*\
(dataMatrix*dataMatrix[j, :].T)) + b
# 然后,基于这个实例的预测结果和真实结果的比对,就可以计算误差Ei 。
# 如果误差很大,那么可以对该数据实例所对应的 alpha 值进行优化
Ej = fXj - float(labelMat[j])
#。这个过程可以通过copy()的方法来实现,因此稍后可以将新的alpha值与老的alpha值进行比较 。
# python会通过引用的方式传递所有列表,所以必须明确地告知 python要为alphaIold和alphaJold
#分配新的内存;否则的话,在对新值和旧值进行比较时,我们就看不到新旧值的变化
alphaIold = alphas[i].copy();
alphaJold = alphas[j].copy();
if(labelMat[i] != labelMat[j]):
#计算 L和 H,它们用于将alphas[j]调整到0到C之间。
L = max(0, alphas[j] - alphas[i])
H = min(C, C + alphas[j] - alphas[i])
else:
L = max(0, alphas[j] + alphas[i] - C)
H = min(C, alphas[j] + alphas[i])
# 如果L和H相等,就不做任何改变,直接执行continue语句
if L == H: print("L==H");continue
#eta是alphas[j]的最优修改量,在那个很长的计算代码行中得到
eta = 2.0*dataMatrix[i,:]*dataMatrix[j,:].T - \
dataMatrix[i,:]*dataMatrix[i,:].T - \
dataMatrix[j,:]*dataMatrix[j,:].T
# 。如果eta为0,那就是说需要退出for循环的当前迭代过程
if eta >= 0: print("eta >=0 "); continue
#于是,可以计算出一个新的alphas[j],
alphas[j] -= labelMat[j]*(Ei - Ej)/eta
#利用clipAlpha()函数以及L与H值对其进行调整。
alphas[j] = clipAlpha(alphas[j], H, L)
#然后,就是需要检查alphas[j]是否有轻微改变。如果是的话,就退出for循环
if (abs(alphas[j] - alphaJold) < 0.00001):print(\
"j not moving enough");continue
#alphas[i] 和alphas[j]同样进行改变,虽然改变的大小一样,但是改变的方向正好相反
# (即如果一个增加,那么另外一个减少)
alphas[i] += labelMat[j]*labelMat[i]*\
(alphaJold - alphas[j])
#。在对alphas[i]和alphas[j]进行优化之后,给这两个alpha值设置一个常数项b
b1 = b - Ei - labelMat[i]*(alphas[i] - alphaIold)*\
dataMatrix[i, :]*dataMatrix[i, :].T - \
labelMat[j]*(alphas[j] - alphaJold)*\
dataMatrix[i, :]*dataMatrix[j, :].T
b2 = b - Ej - labelMat[i] * (alphas[i] - alphaIold) * \
dataMatrix[i, :] * dataMatrix[j, :].T - \
labelMat[j] * (alphas[j] - alphaJold) * \
dataMatrix[j, :] * dataMatrix[j, :].T
if(0 < alphas[i]) and (C > alphas[i]): b = b1
elif (0 < alphas[j]) and (C > alphas[j]): b = b2
else: b = (b1 + b2)/2.0
#最后,在优化过程结束的同时,必须确保在合适的时机结束循环。如果程序执行到for循环
#的最后一行都不执行continue语句,那么就已经成功地改变了一对alpha,同时可以增加
#alphaPairsChanged的值
alphaPairsChanged += 1
print("iter: %d i:%d, pairs changed %d" %\
(iter, i, alphaPairsChanged))
#。在for循环之外,需要检査alpha是否做了更新,如果有更新则将iter设置为0后继续运行程序。
# 只有在所有数据集上遍历maxIter次,且不再发生任何alpha修改之后,程序才会停止并退出for循环。
if(alphaPairsChanged == 0):iter += 1
else: iter = 0
print("iteration number:%d" % iter)
return b, alphas
#测试函数
b,alphas = smoSimple(dataArr, labelArr, 0.6, 0.001, 40)
print("b:",b,'\n',"alpha: ", alphas[alphas>0])
测试结果:
了得到支持向量机的个数 和了解哪些数据点是支持向量
#为了得到支持向量机的个数
print("支持向量机的个数:",shape(alphas[alphas>0]))
#为了了解哪些数据点是支持向量
print("数据点是支持向量:")
for i in range(100):
if alphas[i] > 0.0:
print(dataArr[i], labelArr[i])测试结果:
4.利用完整 Platt SMO 算法加速优化
4.1 完整版 Platt SMO 的支持函数
#利用完整 Platt SMO 算法加速优化
#建立一个init()(构造方法)的optStruct的类来保存所有的重要值
#除了增加了一个 的矩m*2的矩阵成员变量eCache之外 ,这些做法和简化版SMO一模一样。
# eCache的第一列给出的是eCache是否有效的标志位,而第二列给出的是实际的E值。
class optStruct:
##函数有5个输人参数,分别是:默认参数 self、数据集、类别标签、常数C、容错率
def __init__(self, dataMatIn, classLabels, C, toler):
self.X = dataMatIn
self.labelMat = classLabels
self.C = C
self.tol = toler
#shape函数是numpy.core.fromnumeric中的函数,它的功能是查看矩阵或者数组的维数。
#通过numpy库中的shape()函数获取数据集的行数 m
self.m = shape(dataMatIn)[0]
# zeros()函数构建一个alpha列矩阵(m 行 1 列),矩阵中元素都初始化为0
# 调用mat()函数将矩阵转换为numpy矩阵,对矩阵进行一些线性代数的操作,简化很多数学操作
self.alphas = mat(zeros((self.m,1)))
self.b = 0
# zeros()函数构建一个eCache列矩阵(m 行 1 列),矩阵中元素都初始化为0
# 调用mat()函数将矩阵转换为numpy矩阵,对矩阵进行一些线性代数的操作,简化很多数学操作
self.eCache = mat(zeros((self.m,2)))
def calcEk(oS, k):
#对于给定的alpha值,第一个辅助函数calCEk()能够计算E值并返回
fXk = float(multiply(oS.alphas,oS.labelMat).T*\
(oS.X*oS.X[k,:].T)) + oS.b
Ek = fXk - float(oS.labelMat[k])
return Ek
#selectJ()函数用于选择第二个alpha或者说内循环的alpha值
#目标是选择合适的第二个alpha值以保证在每次优化中采用最大步长
def selectJ(i, oS, Ei):
maxK = -1; maxDeltaE = 0; Ej = 0
oS.eCache[i] = [1, Ei]
validEcacheList = nonzero(oS.eCache[:, 0].A)[0]
if(len(validEcacheList)) > 1:
for k in validEcacheList:
if k == i: continue
Ek = calcEk(oS, k)
deltaE = abs(Ei - Ek)
deltaE = abs(Ei - Ek)
if (deltaE > maxDeltaE):
maxK = k; maxDeltaE = deltaE; Ej = Ek
return maxK, Ej
else:
j = selectJrand(i, oS.m)
Ej = calcEk(oS, j)
return j, Ej
#计算误差值存入缓存中
def updateEk(oS, k):
Ek = calcEk(oS, k)
oS.eCache[k] = [1, Ek]4.2 完整Platt SMO算法中的优化例程
#完整Platt SMO 算法中的优化例程
def innerL(i, oS):
Ei = calcEk(oS, i)
if ((oS.labelMat[i]*Ei < -oS.tol) and (oS.alphas[i] < oS.C)) or \
((oS.labelMat[i]*Ei > oS.tol) and (oS.alphas[i] > 0)):
j, Ej = selectJ(i, oS, Ei)
alphaIold = oS.alphas[i].copy(); alphaJold = oS.alphas[j].copy();
if (oS.labelMat[i] != oS.labelMat[j]):
# 计算 L和 H,它们用于将alphas[j]调整到0到C之间。
L = max(0, oS.alphas[j] - oS.alphas[i])
H = min(oS.C, oS.C + oS.alphas[j] - oS.alphas[i])
else:
L = max(0, oS.alphas[j] + oS.alphas[i] - oS.C)
H = min(oS.C, oS.alphas[j] + oS.alphas[i])
# 如果L和H相等,就不做任何改变,直接执行continue语句
if L == H: print("L==H");return 0
# eta是alphas[j]的最优修改量,在那个很长的计算代码行中得到
eta = 2.0 * oS.X[i, :] * oS.X[j, :].T - \
oS.X[i, :] * oS.X[i, :].T - \
oS.X[j, :] * oS.X[j, :].T
# 。如果eta为0,那就是说需要退出for循环的当前迭代过程
if eta >= 0: print("eta >=0 "); return 0
# 于是,可以计算出一个新的alphas[j],
oS.alphas[j] -= oS.labelMat[j] * (Ei - Ej) / eta
# 利用clipAlpha()函数以及L与H值对其进行调整。
oS.alphas[j] = clipAlpha(oS.alphas[j], H, L)
#更新误差缓存
updateEk(oS, j)
# 然后,就是需要检查alphas[j]是否有轻微改变。如果是的话,就退出for循环
if (abs(oS.alphas[j] - alphaJold) < 0.00001): print( \
"j not moving enough");return 0
# alphas[i] 和alphas[j]同样进行改变,虽然改变的大小一样,但是改变的方向正好相反
# (即如果一个增加,那么另外一个减少)
oS.alphas[i] += oS.labelMat[j] * oS.labelMat[i] * \
(alphaJold - oS.alphas[j])
# 更新误差缓存
updateEk(oS, j)
# 。在对alphas[i]和alphas[j]进行优化之后,给这两个alpha值设置一个常数项b
b1 = oS.b - Ei - oS.labelMat[i] * (oS.alphas[i] - alphaIold) * \
oS.X[i, :] * oS.X[i, :].T - \
oS.labelMat[j] * (oS.alphas[j] - alphaJold) * \
oS.X[i, :] * oS.X[j, :].T
b2 = oS.b - Ej - oS.labelMat[i] * (oS.alphas[i] - alphaIold) * \
oS.X[i, :] * oS.X[j, :].T - \
oS.labelMat[j] * (oS.alphas[j] - alphaIold) * \
oS.X[j, :] * oS.X[j, :].T
if (0 < oS.alphas[i]) and ( oS.C > oS.alphas[i]):
oS.b = b1
elif (0 < oS.alphas[j]) and ( oS.C > oS.alphas[j]):
oS.b = b2
else:
oS.b = (b1 + b2) / 2.0
return 1
else: return 0;4.3 完整版Platt SMO的外循环
#完整版 Plat SMO的外循环代码
def smoP(dataMatIn, classLabels, C, toler, maxIter, kTup=('lin', 0)):
#函数一开始构建一个数据结构来容纳所有的数据
oS = optStruct(mat(dataMatIn), mat(classLabels).transpose(), C, toler)
#对控制函数退出的一些变量进行初始化
iter = 0
entireSet = True; alphaPairsChanged = 0;
#1.这里的maxIter变量和函数smoSimple()中的作用有一点不同,后者当没有任何alpha发生改变
#时会将整个集合的一次遍历过程计成一次迭代,而这里的一次迭代定义为一次循环过程,而不管
#该循环具体做了什么事。此时,如果在优化过程中存在波动就会停止,因此这里的做法优于
#smoSimple ()函数中的计数方法。
##2.当迭代次数超过指定的最大值,或者遍历整个集合都未对任意alpna对进行修改时,就退出循环
while (iter < maxIter) and ((alphaPairsChanged > 0) or (entireSet)):
alphaPairsChanged = 0
if entireSet:
#遍历所有的值
for i in range(oS.m):
#过调用innerL()来选择第二个alpha,并在可能时对其进行优化处理
alphaPairsChanged += innerL(i, oS)
print("fullSet, iter: %d i:%d, pairs changed %d" %\
(iter, i ,alphaPairsChanged))
iter +=1
else:
nonBundIs = nonzero((oS.alphas.A > 0)*(oS.alphas.A < C))[0]
#循环遍历所有的非边界alpha值,,也就是不在边界0或C上的值
for i in nonBundIs:
alphaPairsChanged += innerL(i, oS)
print("non-bound, iter: %d i:%d, pairs changed %d" % \
(iter, i, alphaPairsChanged))
iter += 1
if entireSet: entireSet = False_
elif (alphaPairsChanged == 0): entireSet = True
print("iteration number: %d" % iter)
return oS.b, oS.alphas
#测试函数
dataArr, labelArr =loadDataSet('testSet.txt')
b, alphas = smoP(dataArr, labelArr, 0.6, 0.001, 40)测试结果:
5 .在复杂数据上应用核函数
5.1 径向基核函数
#在复杂数据集上应用核函数
#核转换函数
def kernelTrans(X, A, kTup):
# 通过numpy 库的shape()函数得到数据集的 行数和列数 (m ,n)
m,n = shape(X)
# 通过numpy 库中的zeros()函数构建一个alpha列矩阵(m 行 1 列),矩阵中元素都初始化为0
# 通过numpy 库中的mat()函数将矩阵转换为numpy矩阵,对矩阵进行一些线性代数的操作,简化很多数学操作
K = mat(zeros((m,1)))
if kTup[0] == 'lin': K = X*A.T
elif kTup[0] == 'rbf':
#python range() 函数可创建一个整数列表
for j in range(m):
deltaRow = X[j, :] - A
K[j] = deltaRow*deltaRow.T
K = exp(K /(-1*kTup[1]**2))
else: raise NameError('Houston We Have a Proble -- That Kernel is not recognized')
return K
#对opStruct进行改造
class optStruct:
##函数有5个输人参数,分别是:默认参数 self、数据集、类别标签、常数C、容错率
#kTup是一个包含核函数信息‘的元组
def __init__(self, dataMatIn, classLabels, C, toler, kTup):
self.X = dataMatIn
self.labelMat = classLabels
self.C = C
self.tol = toler
#shape函数是numpy.core.fromnumeric中的函数,它的功能是查看矩阵或者数组的维数。
#通过numpy库中的shape()函数获取数据集的行数 m
self.m = shape(dataMatIn)[0]
# zeros()函数构建一个alpha列矩阵(m 行 1 列),矩阵中元素都初始化为0
# 调用mat()函数将矩阵转换为numpy矩阵,对矩阵进行一些线性代数的操作,简化很多数学操作
self.alphas = mat(zeros((self.m,1)))
self.b = 0
# zeros()函数构建一个eCache列矩阵(m 行 1 列),矩阵中元素都初始化为0
# 调用mat()函数将矩阵转换为numpy矩阵,对矩阵进行一些线性代数的操作,简化很多数学操作
self.eCache = mat(zeros((self.m,2)))
#矩阵K被构建,然后再通过调用函数kernelTrans()进行填充。全局的K值只需计算一次。
# 然后,当想要使用核函数时,就可以对它进行调用。这也省去了很多冗余的计算开销。
self.K = mat(zeros((self.m, self.m)))
for i in range(self.m):
self.K[:, i] = kernelTrans(self.X, self.X[i, :], kTup)
建议读者最好看一下optStruct类的新版本。除了引人了一个新变量kTup之外,该版本和原来的optStruct一模一样
5.2 为了使用核函数,先期的两个函数innerL()和calcEk()的代码需要做些修改
#修改后的代码:
#完整Platt SMO 算法中的优化例程
def innerL(i, oS):
Ei = calcEk(oS, i)
if ((oS.labelMat[i]*Ei < -oS.tol) and (oS.alphas[i] < oS.C)) or ((oS.labelMat[i]*Ei > oS.tol) and (oS.alphas[i] > 0)):
j, Ej = selectJ(i, oS, Ei)
alphaIold = oS.alphas[i].copy(); alphaJold = oS.alphas[j].copy();
if (oS.labelMat[i] != oS.labelMat[j]):
# 计算 L和 H,它们用于将alphas[j]调整到0到C之间。
L = max(0, oS.alphas[j] - oS.alphas[i])
H = min(oS.C, oS.C + oS.alphas[j] - oS.alphas[i])
else:
L = max(0, oS.alphas[j] + oS.alphas[i] - oS.C)
H = min(oS.C, oS.alphas[j] + oS.alphas[i])
# 如果L和H相等,就不做任何改变,直接执行continue语句
if L == H: print("L==H");return 0
# eta是alphas[j]的最优修改量,在那个很长的计算代码行中得到
eta = 2.0 * oS.K[i, j] * oS.K[i, i] - oS.K[j,j]
# 。如果eta为0,那就是说需要退出for循环的当前迭代过程
if eta >= 0: print("eta >=0 "); return 0
# 于是,可以计算出一个新的alphas[j],
oS.alphas[j] -= oS.labelMat[j] * (Ei - Ej) / eta
# 利用clipAlpha()函数以及L与H值对其进行调整。
oS.alphas[j] = clipAlpha(oS.alphas[j], H, L)
#更新误差缓存
updateEk(oS, j)
# 然后,就是需要检查alphas[j]是否有轻微改变。如果是的话,就退出for循环
if (abs(oS.alphas[j] - alphaJold) < 0.00001): print("j not moving enough");return 0
# alphas[i] 和alphas[j]同样进行改变,虽然改变的大小一样,但是改变的方向正好相反
# (即如果一个增加,那么另外一个减少)
oS.alphas[i] += oS.labelMat[j] * oS.labelMat[i] * (alphaJold - oS.alphas[j])
# 更新误差缓存
updateEk(oS, j)
# 。在对alphas[i]和alphas[j]进行优化之后,给这两个alpha值设置一个常数项b
b1 = oS.b - Ei - oS.labelMat[i] * (oS.alphas[i] - alphaIold) * oS.K[i, i] - oS.labelMat[j] * (oS.alphas[j] - alphaJold) * oS.K[i, j]
b2 = oS.b - Ej - oS.labelMat[i] * (oS.alphas[i] - alphaIold) * oS.K[i, j] - oS.labelMat[j] * (oS.alphas[j] - alphaJold) * oS.K[j, j]
if (0 < oS.alphas[i]) and ( oS.C > oS.alphas[i]):
oS.b = b1
elif (0 < oS.alphas[j]) and ( oS.C > oS.alphas[j]):
oS.b = b2
else:
oS.b = (b1 + b2) / 2.0
return 1
else: return 0;
#修改后的 calcEk()
def calcEk(oS, k):
#对于给定的alpha值,第一个辅助函数calCEk()能够计算E值并返回
fXk = float(multiply(oS.alphas,oS.labelMat).T*oS.K[:, k] + oS.b)
Ek = fXk - float(oS.labelMat[k])
return Ek
5.3 在测试中使用核函数
#在测试中使用核函数
#该输人参数是高斯径向基函数中的一个用户定义变量
def testRbf(k1 =1.3):
#程序从文件中读人数据集
dataArr, labelArr = loadDataSet("testSetRBF.txt")
#在该数据集上运行PlattSMO算法,其中核函数的类型为'rbf'
b, alphas = smoP(dataArr, labelArr, 200, 0.0001, 10000, ('rbf', k1))
#优化过程结束后,在后面的矩阵数学运算中建立数据的矩阵副本
datMat = mat(dataArr); labelMat = mat(labelArr).transpose()
#且找出那些非零的alpha值,从而得到所需要的支持向量
svInd = nonzero(alphas.A > 0)[0]
#同时,也就得到了这些支持向量和alpha的类别标签值
sVs = datMat[svInd]
labelSV = labelMat[svInd];
print("there are %d Support Vector" % shape(sVs)[0])
m, n = shape(datMat)
errorCount = 0;
for i in range(m):
#首先利用结构初始化方法中使用过的kernelTrans()函数,得到转换后的数据
kernelEval = kernelTrans(sVs, datMat[i, :],('rbf',k1))
#然后,再用其与前面的alpha及类别标签值求积。其中需要特别注意的另一件事是,
# 在这几行代码中,是如何做到只需要支持向量数据就可以进行分类的。除此之外,
# 其他数据都可以直接舍弃。
predict = kernelEval.T*multiply(labelSV, alphas[svInd]) + b
if sign(predict) != sign(labelArr[i]): errorCount += 1
print("the training error rate is: %f" % (float(errorCount)/m))
##程序从测试数据集文件中读人数据集
dataArr, labelArr = loadDataSet('testSetRBF2.txt')
errorCount = 0
#1.在后面的矩阵数学运算中建立数据的矩阵副本,
##2.并用通过numpy 库中的mat()函数将矩阵转换为numpy矩阵,对矩阵进行一些线性代数的操作,
# 简化很多数学操作
datMat = mat(dataArr); labelMat = mat(labelArr).transpose()
#通过numpy 库的shape()函数得到数据集的 行数和列数 (m ,n)
m, n = shape(datMat)
for i in range(m):
# 首先利用结构初始化方法中使用过的kernelTrans()函数,得到转换后的数据
kernelEval = kernelTrans(sVs, datMat[i, :], ('rbf', k1))
# 然后,再用其与前面的alpha及类别标签值求积。其中需要特别注意的另一件事是,
# 在这几行代码中,是如何做到只需要支持向量数据就可以进行分类的。除此之外,
# 其他数据都可以直接舍弃。
predict = kernelEval.T*multiply(labelSV, alphas[svInd]) + b
if sign(predict) != sign(labelArr[i]):errorCount += 1
print("the test error rate is: %f" % (float(errorCount)/m))
#测试函数
testRbf()测试结果截图:
书上源代码测试截图:
从图中可以发现错误率相差太多,我检查了很多遍代码还是没找到原因。
6.手写识别问题回顾
6.1 示例:基于曰SVM的数宇识别
(1)收集数据:提供的文本文件。
(2)准备数据:基于二值图像构造向量。
(3)分析数据:对图像向量进行目测。
(4)训练算法:采用两种不同的核函数,并对径向基核函数采用不同的设置来运行SMO算法。
(5)测试算法:编写一个函数来测试不同的核函数并计算措误率。
(6)使用算法:一个图像识别的完整应用还需要一些图像处理的知识,这里并不打算深入介绍。
6.2 基于SVM的手写数字识别
"""
手写数据集 准备数据:将图像转换为测试向量
"""
def img2vector(filename):
returnVect = zeros((1,1024))
fr = open(filename)
for i in range(32):
lineStr = fr.readline()
for j in range(32):
returnVect[0, 32*i+j] = int(lineStr[j])
#返回数组
return returnVect
#基于SVM的手写数字识别
def loadImages(dirName):
from os import listdir
hwLabels = []
trainingFileList = listdir(dirName)
m = len(trainingFileList)
trainingMat = zeros((m,1024))
for i in range(m):
fileNameStr = trainingFileList[i]
fileStr = fileNameStr.split('.')[0]
classNumStr = int(fileStr.split('_')[0])
if classNumStr == 9: hwLabels.append(-1)
else: hwLabels.append(1)
trainingMat[i,:] = img2vector('%s/%s' % (dirName, fileNameStr))
return trainingMat, hwLabels
def testDigits(kTup =('rbf',10)):
dataArr , labelArr = loadImages('trainingDigits')
b, alphas = smoP(dataArr, labelArr, 200, 0.0001, 10000, kTup)
datMat = mat(dataArr)
labelMat = mat(labelArr).transpose()
# 且找出那些非零的alpha值,从而得到所需要的支持向量
svInd = nonzero(alphas.A > 0)[0]
# 同时,也就得到了这些支持向量和alpha的类别标签值
sVs = datMat[svInd]
labelSV = labelMat[svInd];
print("there are %d Support Vector" % shape(sVs)[0])
m, n = shape(datMat)
errorCount = 0;
for i in range(m):
# 首先利用结构初始化方法中使用过的kernelTrans()函数,得到转换后的数据
kernelEval = kernelTrans(sVs, datMat[i, :], kTup)
# 然后,再用其与前面的alpha及类别标签值求积。其中需要特别注意的另一件事是,
# 在这几行代码中,是如何做到只需要支持向量数据就可以进行分类的。除此之外,
# 其他数据都可以直接舍弃。
predict = kernelEval.T * multiply(labelSV, alphas[svInd]) + b
if sign(predict) != sign(labelArr[i]): errorCount += 1
print("the training error rate is: %f" % (float(errorCount) / m))
##程序从测试数据集文件中读人数据集
dataArr, labelArr = loadImages('testDigits')
errorCount = 0
# 1.在后面的矩阵数学运算中建立数据的矩阵副本,
##2.并用通过numpy 库中的mat()函数将矩阵转换为numpy矩阵,对矩阵进行一些线性代数的操作,
# 简化很多数学操作
datMat = mat(dataArr);
labelMat = mat(labelArr).transpose()
# 通过numpy 库的shape()函数得到数据集的 行数和列数 (m ,n)
m, n = shape(datMat)
for i in range(m):
# 首先利用结构初始化方法中使用过的kernelTrans()函数,得到转换后的数据
kernelEval = kernelTrans(sVs, datMat[i, :], kTup)
# 然后,再用其与前面的alpha及类别标签值求积。其中需要特别注意的另一件事是,
# 在这几行代码中,是如何做到只需要支持向量数据就可以进行分类的。除此之外,
# 其他数据都可以直接舍弃。
predict = kernelEval.T * multiply(labelSV, alphas[svInd]) + b
if sign(predict) != sign(labelArr[i]): errorCount += 1
print("the test error rate is: %f" % (float(errorCount) / m))
#测试函数
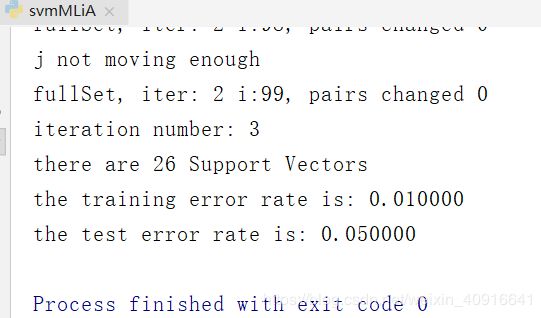
testDigits(('rbf',20))
end = time.process_time()
print( "read: %f s" % (end - start))
测试结果: