【JZOJ100048】紧急撤离
JZOJ100048.【NOIP2017提高A组模拟7.14】紧急撤离
Time Limits: 1000 ms Memory Limits: 256 MB
Description
某日, 敌军对某村落展开攻击,所幸我情报部门提前预知了消息,村民兵武装连夜组织村民快速转移,为此他们需要赶往地道入口。已知村庄形成了 N * M 的方格网络,周围被封锁,无法穿行。其中有些方格没有敌军占领,可以进入,有些方格已经被敌军渗透,不能进入。由于敌军的步步紧逼,民众只能向行或列增大的地方移动:即(x, y) → (x + 1, y)或(x, y) → (x, y + 1)。 机智的 Star 手提笔记本,正和民兵队长商议对策。民兵队长会问你 Q 个问 题,每个问题均类似于坐标(a, b)的村民能否安全到达位于坐标(c, d)的地道(队长是机智的,他的问题总保证起点和终点均安全),你需要赶快写出程序来帮助他。
Input
第 1 行两个整数 N, M;
第 2 ~ n + 1 行给出一个 N * M 的 0/1 矩形(每行可看作一字符串),其中 0 表示安全,1 表示不安全,设第 i + 1 行第 j 列的位置坐标为(i, j)。
第 n + 2 行一个整数 Q;
接下来 Q 行每行四个整数 a、b、c、d,保证坐标合法。
Output
对于每组询问,输出一行“Safe”或“Dangerous”。
Sample Input
7 7
0100000
0000010
0001010
0011000
1000010
0000000
0111001
5
3 3 4 6
6 1 6 7
4 5 6 5
3 3 4 5
4 6 7 6
Sample Output
Dangerous
Safe
Safe
Dangerous
Dangerous
Data Constraint
对于 20%的数据,n, m ≤ 50;
对于另外 20%的数据,n, m ≤ 200、q ≤ 1000;
对于 100%的数据,n, m ≤ 500、q ≤ 600000。
题目大意
给一个01矩阵,q个询问(x,y,X,Y)问是否能不经过1点只向下或右从(x,y)走到(X,Y)
样例:

解题思路
前20%数据:预处理所有(x,y)能到达的点,每个询问O(1)回答 O(n2m2+q)
接下来20%数据,对于每个询问直接暴力是否能到达, O(qnm)
100%:
我们想, (x,y) 能到达 (x1,y1) 的充分必要条件是:
假设有集合S{(x′,y′)|(x,y)可以到达(x′,y′)},T{(x′′,y′′)|(x′′,y′′)可以到达(x1,y1)},对于路径(x,y)(x1,y1)上的任意一点P(x0,y0)有P∈S,P∈T
分治!
对于二维区间 [1,n][h,t] 我们取中间列 [1,n][mid,mid] ,将能通过中间列的答案求出,然后分治 [1,n][h,mid−1]和[1,n][mid+1,t] 具体方法如下:
我们逆序求出 区间[1,n][h,mid] 的点分别可以到达那些中间列的位置,设为集合A(x,y),求出 区间[1,n][mid+1,t] 的点分别可以被那些中间列的点到达,设为集合B(x,y)。

对于跨过中间列的询问(x,y,X,Y)若 A(x,y)∩B(X,Y)≠∅ 则说明(x,y)可以到达(X,Y)
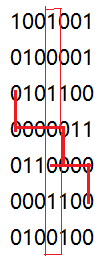
处理答案呢? O(qnlogn) ?
我们以Y从大到小建数组模拟链表,若某个 Y′<m 就可以停了,并将之前搜的删除
有一种特殊状况!!

当Y=m的情况,在图中,我们预处理时可能得到 A(2,1)={2,3,5,6},A(5,5)={5,6} 然而(2,1)不能到达(5,5)
所以一开始放掉这种情况
最后把mid行重新赋值,再考虑这种情况。
算下时间复杂度:
分治 O(nmlogm∗n) ,求答案 O(qn) ,排序 O(qlogq)
总共 O(n2mlogm+qn+qlogq) T飞了(TLE)!
我们想想,储存集合就要用 O(n) ,如何减少对集合求并求交——开外挂!!
集合 → 二进制 → bitset!!!
加个bitset,优化二进制的运算!
O(n2mlogm+qnω+qlogq)
#includeint read(){
int ans;char ch;for(;(ch=getchar())>'9' || ch<'0';);ans=ch-'0';
for(;(ch=getchar())>='0' && ch<='9';)ans=(ans<<1)+(ans<<3)+(ch-'0');return ans;
}
void dg(int h,int t){
int m=(h+t)>>1;if(h>t)return;
for(int i=1;i<=n;i++)for(int j=h;j<=t;j++)a[i][j]=emp;
for(int i=1;i<=n;i++)if(!map[i][m])a[i][m][i]=1;
for(int i=1;i<=n;i++)for(int j=m+1;j<=t;j++)if(!map[i][j])a[i][j]=a[i-1][j] | a[i][j-1];
for(int i=n;i;i--)for(int j=m;j>=h;j--)if(!map[i][j]){
if(j1][j] | a[i][j+1];else a[i][j]=a[i][j] | a[i+1][j];
}
for(int i=1;i<=n;i++)if(!map[i][m])a[i][m]=emp,a[i][m][i]=1;
for(int i=n;i;i--)for(int j=m-1;j>=h;j--)if(!map[i][j]){
for(int x=fir[i][j];x && qry[x].Y>=m;x=qry[x].nex){
temp=a[qry[x].x][qry[x].y] & a[qry[x].X][qry[x].Y];
if(temp.any())ans[qry[x].w]=1;else ans[qry[x].w]=0;
fir[i][j]=qry[x].nex;
}
}
for(int i=n;i;i--)for(int j=m;j<=m;j++)if(!map[i][j]){
a[i][j]=a[i][j]|a[i+1][j];
for(int x=fir[i][j];x && qry[x].Y>=m;x=qry[x].nex){
temp=a[qry[x].x][qry[x].y] & a[qry[x].X][qry[x].Y];
if(temp.any())ans[qry[x].w]=1;else ans[qry[x].w]=0;
fir[i][j]=qry[x].nex;
}
}
dg(h,m-1);dg(m+1,t);
}
int main(){
scanf("%d %d\n",&n,&m);
for(int i=1;i<=n;i++,scanf("\n"))for(int j=1;j<=m;j++)map[i][j]=(getchar()-'0');
scanf("%d",&q);for(int i=1;i<=q;i++)qry[i].x=read(),qry[i].y=read(),qry[i].X=read(),qry[i].Y=read(),qry[i].w=i;
sort(qry+1,qry+q+1,cmp);
for(int i=1;i<=q;i++){
int x=qry[i].x,y=qry[i].y;
if(x<=qry[i].X && y<=qry[i].Y)qry[i].nex=fir[x][y],fir[x][y]=i;else ans[qry[i].w]=0;
}
dg(1,m);
for(int i=1;i<=q;i++)if(ans[i])printf("Safe\n");else printf("Dangerous\n");
return 0;
} bitset的一些用法:
函数库#include
定义bitset
bitset可以像变量一样进行位运算
查询单个位B[]
1. 判断非全为0B.any()
2. 判断全为0B.none()
3. 求二进制位为1的个数B.count()
4. 求二进制位的个数B.size()
5. 判断pos位为1B.test(pos)
6. 整体赋值1B.set()
7. pos位赋为1B.set(pos)
8. 整体赋值0B.reset()
9. pos位赋为0B.reset(pos)
10. 整体取反B.flip()
11. pos位取反B.flip(pos)