时间序列相似性度量-DTW
1. 背景
最近项目中遇到求解时间序列相似性问题,这里序列也可以看成向量。在传统算法中,可以用余弦相似度和pearson相关系数来描述两个序列的相似度。但是时间序列比较特殊,可能存在两个问题:
- 两段时间序列长度不同。如何求相似度?
- 一个序列是另一个序列平移之后得到的。如何求相似距离?
第一个问题,导致了根本不能用余弦相似度和pearson相关系数来求解相似。第二个问题,导致了也不能基于欧式距离这样的算法,来求解相似距离。比如下面两个长度不同的序列:
s1 = [1, 2, 0, 1, 1, 2]
s2 = [1, 0, 1]
本文记录一种算法,一方面:如果两个序列中的其中一个序列是另一个序列的平移序列,则可以比较合理的求出两个序列的相似距离。另一方面:也可以求解长度不同序列的相似距离。主要参考:dtaidistance 这个项目的源码和其中的Dynamic Time Warping (DTW)思想。
同时基于这个算法,先计算相似距离,再把相似距离通过 1 1 + d i s t \frac{1}{1+dist} 1+dist1 转化为相似度。这样就可以得到长度不同向量的相似度。
2. 核心思想
Dynamic Time Warping (DTW) 本质上和通过动态规划来计算这个序列的相似距离。其实这和求解字符串的最长公共子串、子序列这类问题本质比较类似,参考:
- 两个字符串的最长子串
- 两个字符串的最长子序列
这里基于动态规划构建序列a和序列b的距离矩阵dp[i][j],其中dp[i][j]表示序列a[0:i]和b[0:j]之间的相似距离的平方。并且有:
d p [ i ] [ j ] = { ( a [ 0 ] − b [ 0 ] ) 2 i = 0, j = 0 ( a [ 0 ] − b [ j ] ) 2 + d p [ 0 ] [ j − 1 ] i = 0 ( a [ i ] − b [ 0 ] ) 2 + d p [ i − 1 ] [ 0 ] j = 0 ( a [ i ] − b [ j ] ) 2 + m i n ( d p [ i − 1 ] [ j ] , d p [ j − 1 ] [ i ] , d p [ i − 1 ] [ j − 1 ] ) i , j > 0 dp[i][j] = \begin{cases} (a[0] - b[0])^2 \quad\quad &\text{i = 0, j = 0} \\ (a[0] - b[j])^2 + dp[0][j-1] \quad\quad &\text{i = 0} \\ (a[i] - b[0])^2 + dp[i-1][0] \quad\quad &\text{j = 0} \\ (a[i] - b[j])^2 + min(dp[i-1][j],dp[j-1][i],dp[i-1][j-1]) \quad\quad &i,j > 0 \end{cases} dp[i][j]=⎩⎪⎪⎪⎨⎪⎪⎪⎧(a[0]−b[0])2(a[0]−b[j])2+dp[0][j−1](a[i]−b[0])2+dp[i−1][0](a[i]−b[j])2+min(dp[i−1][j],dp[j−1][i],dp[i−1][j−1])i = 0, j = 0i = 0j = 0i,j>0
所以dp[len(a)-1][len(b)-1] 就是相似距离的平方,最后开方就是两个时间序列的相似距离,这也就是DTW算法核心实现。实际上,上文的那个github核心代码其实也就是这么写的,只不过在此基础上加了其他参数、画图、层次聚类的代码实现而已。
3. 实现
在实际使用中解读了dtaidistance这个项目的源码,其中除去所有参数后,DTW最简单的实现如下:
import numpy as np
float_formatter = lambda x: "%.2f" % x
np.set_printoptions(formatter={'float_kind': float_formatter})
def TimeSeriesSimilarity(s1, s2):
l1 = len(s1)
l2 = len(s2)
paths = np.full((l1 + 1, l2 + 1), np.inf) # 全部赋予无穷大
paths[0, 0] = 0
for i in range(l1):
for j in range(l2):
d = s1[i] - s2[j]
cost = d ** 2
paths[i + 1, j + 1] = cost + min(paths[i, j + 1], paths[i + 1, j], paths[i, j])
paths = np.sqrt(paths)
s = paths[l1, l2]
return s, paths.T
if __name__ == '__main__':
s1 = [1, 2, 0, 1, 1, 2]
s2 = [1, 0, 1]
distance, paths = TimeSeriesSimilarity(s1, s2)
print(paths)
print("=" * 40)
print(distance)
输出
[[0.00 inf inf inf inf inf inf]
[inf 0.00 1.00 1.41 1.41 1.41 1.73]
[inf 1.00 2.00 1.00 1.41 1.73 2.45]
[inf 1.00 1.41 1.41 1.00 1.00 1.41]]
========================================
1.4142135623730951
这里的矩阵
[ 0.00 1.00 1.41 1.41 1.41 1.73 1.00 2.00 1.00 1.41 1.73 2.45 1.00 1.41 1.41 1.00 1.00 1.41 ] \begin{bmatrix} 0.00 & 1.00 & 1.41 & 1.41 & 1.41 & 1.73 \\ 1.00 & 2.00 & 1.00 & 1.41 & 1.73 & 2.45 \\ 1.00 & 1.41 & 1.41 & 1.00 & 1.00 & 1.41 \end{bmatrix} ⎣⎡0.001.001.001.002.001.411.411.001.411.411.411.001.411.731.001.732.451.41⎦⎤
就是dp[i][j]。这里代码用另一种写法实现了求解dp[i][j]。并且矩阵右下角元素1.41,就是我们求解的相似距离。
4. 改进
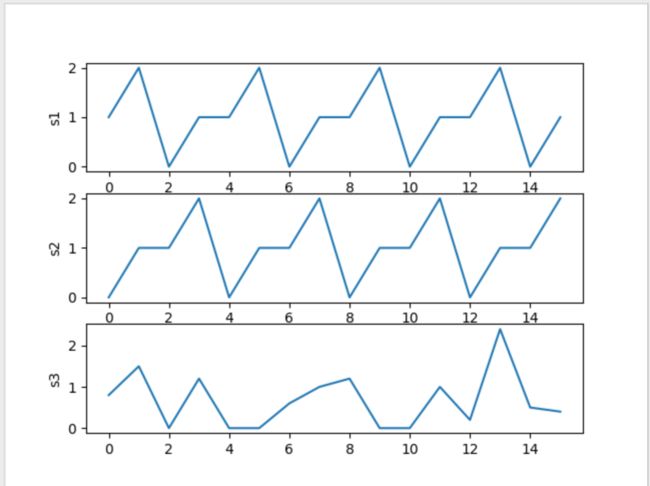
其实在实际使用中,我们发现该算法对周期序列的距离计算不是很好。尤其两个序列是相同周期,但是是平移后的序列。如下:
s1 = np.array([1, 2, 0, 1, 1, 2, 0, 1, 1, 2, 0, 1, 1, 2, 0, 1])
s2 = np.array([0, 1, 1, 2, 0, 1, 1, 2, 0, 1, 1, 2, 0, 1, 1, 2])
s3 = np.array([0.8, 1.5, 0, 1.2, 0, 0, 0.6, 1, 1.2, 0, 0, 1, 0.2, 2.4, 0.5, 0.4])
用图表展示:
很明显从图中可以看到 s 1 s_1 s1和 s 2 s_2 s2是相同的时间序列,但是 s 1 s_1 s1是 s 2 s_2 s2平移后得到的, s 3 s_3 s3是我随意构造的一个序列。但是,现在用上面的算法求解,得:
d i s t ( s 1 , s 2 ) = 2.0 d i s t ( s 1 , s 3 ) = 1.794435844492636 \begin{aligned} dist(s_1,s_2) &= 2.0 \\ dist(s_1,s_3) &= 1.794435844492636 \end{aligned} dist(s1,s2)dist(s1,s3)=2.0=1.794435844492636
我们发现 s 1 s_1 s1和 s 3 s_3 s3反而比较像,这是我们不能接受的。因此,这里需要对算法有个改进。以下有两个改进策略。
4.1 改进策略1
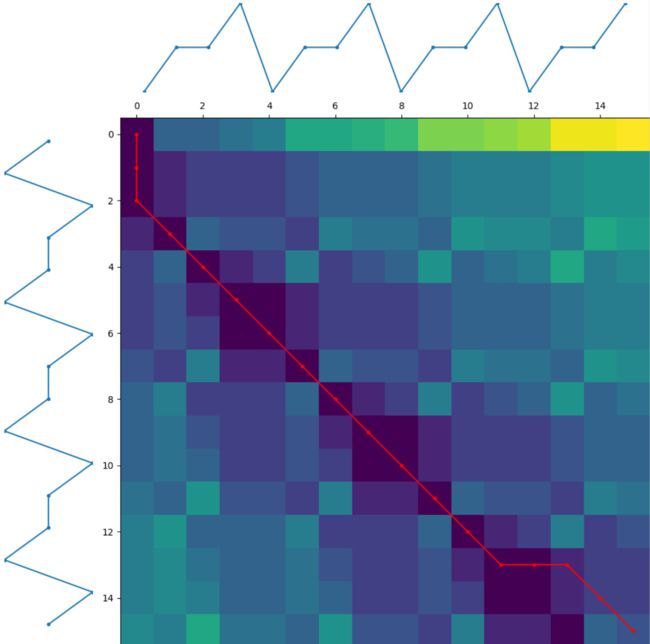
目的是想求得一个惩罚系数 α \alpha α,这个 α \alpha α和原算法的distance相乘,得到更新后的distance。首先基于原算法包dtaidistance,可以求出dp[i][j]从左上角,到右下角的最优路径。
其实这样的最优路径,可以用图示表示,比如 s 1 s_1 s1和 s 2 s_2 s2的dp[i][j]的最优路径:
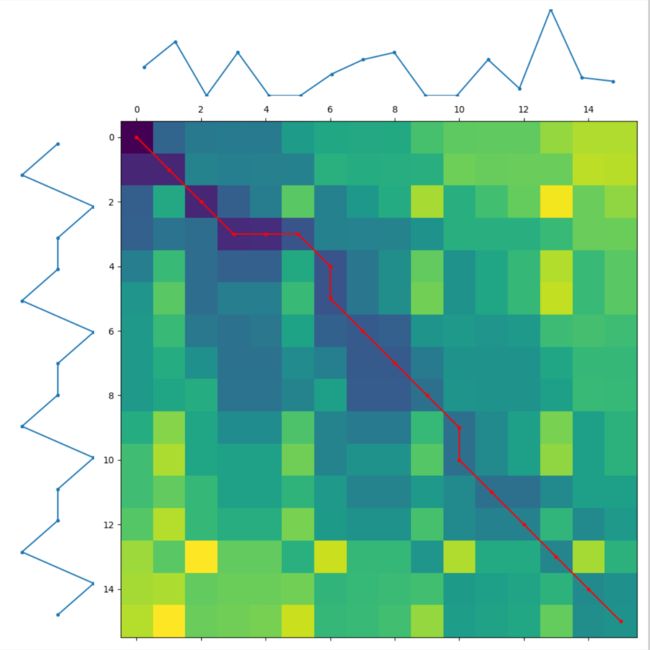
再比如 s 1 s_1 s1和 s 3 s_3 s3的dp[i][j]的最优路径:
其实可以很明显看到, s 1 s_1 s1和 s 2 s_2 s2的最优路径拐点比较少,对角直线很长。而 s 1 s_1 s1和 s 3 s_3 s3的拐点比较多,对角直线很短。因此我基于这个考虑进行优化,公式如下:
α = 1 − ∑ i = 1 n c o m L e n i 2 s e q L e n 2 \alpha = 1- \sqrt{\sum_{i=1}^n \frac{comLen_i^2}{seqLen^2}} α=1−i=1∑nseqLen2comLeni2
其中seqLen 是这个图中最优路径节点个数, c o m L e n i comLen_i comLeni表示每段对角直线的长度。求和后开发表示一个长度系数,这个长度系数越大,表示对角直线越长。最后1减去这个长度系数得到,我们要的衰减系数 α \alpha α。以下是代码实现:
说明:这里best_path()是直接摘自dtaidistance,TimeSeriesSimilarity()方法是修改自这个项目。
import numpy as np
import math
def get_common_seq(best_path, threshold=1):
com_ls = []
pre = best_path[0]
length = 1
for i, element in enumerate(best_path):
if i == 0:
continue
cur = best_path[i]
if cur[0] == pre[0] + 1 and cur[1] == pre[1] + 1:
length = length + 1
else:
com_ls.append(length)
length = 1
pre = cur
com_ls.append(length)
return list(filter(lambda num: True if threshold < num else False, com_ls))
def calculate_attenuate_weight(seqLen, com_ls):
weight = 0
for comlen in com_ls:
weight = weight + (comlen * comlen) / (seqLen * seqLen)
return 1 - math.sqrt(weight)
def best_path(paths):
"""Compute the optimal path from the nxm warping paths matrix."""
i, j = int(paths.shape[0] - 1), int(paths.shape[1] - 1)
p = []
if paths[i, j] != -1:
p.append((i - 1, j - 1))
while i > 0 and j > 0:
c = np.argmin([paths[i - 1, j - 1], paths[i - 1, j], paths[i, j - 1]])
if c == 0:
i, j = i - 1, j - 1
elif c == 1:
i = i - 1
elif c == 2:
j = j - 1
if paths[i, j] != -1:
p.append((i - 1, j - 1))
p.pop()
p.reverse()
return p
def TimeSeriesSimilarity(s1, s2):
l1 = len(s1)
l2 = len(s2)
paths = np.full((l1 + 1, l2 + 1), np.inf) # 全部赋予无穷大
paths[0, 0] = 0
for i in range(l1):
for j in range(l2):
d = s1[i] - s2[j]
cost = d ** 2
paths[i + 1, j + 1] = cost + min(paths[i, j + 1], paths[i + 1, j], paths[i, j])
paths = np.sqrt(paths)
s = paths[l1, l2]
return s, paths.T
if __name__ == '__main__':
# 测试数据
s1 = np.array([1, 2, 0, 1, 1, 2, 0, 1, 1, 2, 0, 1, 1, 2, 0, 1])
s2 = np.array([0, 1, 1, 2, 0, 1, 1, 2, 0, 1, 1, 2, 0, 1, 1, 2])
s3 = np.array([0.8, 1.5, 0, 1.2, 0, 0, 0.6, 1, 1.2, 0, 0, 1, 0.2, 2.4, 0.5, 0.4])
# 原始算法
distance12, paths12 = TimeSeriesSimilarity(s1, s2)
distance13, paths13 = TimeSeriesSimilarity(s1, s3)
print("更新前s1和s2距离:" + str(distance12))
print("更新前s1和s3距离:" + str(distance13))
best_path12 = best_path(paths12)
best_path13 = best_path(paths13)
# 衰减系数
com_ls1 = get_common_seq(best_path12)
com_ls2 = get_common_seq(best_path13)
# print(len(best_path12), com_ls1)
# print(len(best_path13), com_ls2)
weight12 = calculate_attenuate_weight(len(best_path12), com_ls1)
weight13 = calculate_attenuate_weight(len(best_path13), com_ls2)
# 更新距离
print("更新后s1和s2距离:" + str(distance12 * weight12))
print("更新后s1和s3距离:" + str(distance13 * weight13))
输出:
更新前s1和s2距离:2.0
更新前s1和s3距离:1.794435844492636
更新后s1和s2距离:0.6256314581274465
更新后s1和s3距离:0.897217922246318
结论:
用新的算法更新后,我们会发现s1和s2距离比s1和s3的距离更加接近了,这就是我们要的结果。
4.2 改进策略2
也想求得一个惩罚系数 α \alpha α。方案如下:
- 先求解两个序列seq1和seq2的最长公共子串,长度记为a。
- 因为seq1和seq2是数值序列,在求最长公共子串时,设置了一个最大标准差的偏移容忍。也就是说,两个数值在这个标准差内,认为也是公共子串中的一部分。
- 衰减系数: α = 1 − a × a l e n ( s e q 1 ) × l e n ( s e q 2 ) \alpha = 1 - \frac{a \times a}{len(seq1) \times len(seq2)} α=1−len(seq1)×len(seq2)a×a
也就是说,两个数值序列的最长公共子串越长,则衰减系数越小。这里把:s2 = np.array([0, 1, 1, 2, 0, 1, 1, 2, 0, 1, 1, 2, 0, 1, 1, 2])改成s2 = np.array([0, 1, 1, 2, 0, 1, 1.7, 2, 0, 1, 1, 2, 0, 1, 1, 2]),来验证最大标准差的偏移容忍。
实际代码实现和效果如下:
import numpy as np
float_formatter = lambda x: "%.2f" % x
np.set_printoptions(formatter={'float_kind': float_formatter})
def TimeSeriesSimilarityImprove(s1, s2):
# 取较大的标准差
sdt = np.std(s1, ddof=1) if np.std(s1, ddof=1) > np.std(s2, ddof=1) else np.std(s2, ddof=1)
# print("两个序列最大标准差:" + str(sdt))
l1 = len(s1)
l2 = len(s2)
paths = np.full((l1 + 1, l2 + 1), np.inf) # 全部赋予无穷大
sub_matrix = np.full((l1, l2), 0) # 全部赋予0
max_sub_len = 0
paths[0, 0] = 0
for i in range(l1):
for j in range(l2):
d = s1[i] - s2[j]
cost = d ** 2
paths[i + 1, j + 1] = cost + min(paths[i, j + 1], paths[i + 1, j], paths[i, j])
if np.abs(s1[i] - s2[j]) < sdt:
if i == 0 or j == 0:
sub_matrix[i][j] = 1
else:
sub_matrix[i][j] = sub_matrix[i - 1][j - 1] + 1
max_sub_len = sub_matrix[i][j] if sub_matrix[i][j] > max_sub_len else max_sub_len
paths = np.sqrt(paths)
s = paths[l1, l2]
return s, paths.T, [max_sub_len]
def calculate_attenuate_weight(seqLen1, seqLen2, com_ls):
weight = 0
for comlen in com_ls:
weight = weight + comlen / seqLen1 * comlen / seqLen2
return 1 - weight
if __name__ == '__main__':
# 测试数据
s1 = np.array([1, 2, 0, 1, 1, 2, 0, 1, 1, 2, 0, 1, 1, 2, 0, 1])
s2 = np.array([0, 1, 1, 2, 0, 1, 1.7, 2, 0, 1, 1, 2, 0, 1, 1, 2])
s3 = np.array([0.8, 1.5, 0, 1.2, 0, 0, 0.6, 1, 1.2, 0, 0, 1, 0.2, 2.4, 0.5, 0.4])
# 原始算法
distance12, paths12, max_sub12 = TimeSeriesSimilarityImprove(s1, s2)
distance13, paths13, max_sub13 = TimeSeriesSimilarityImprove(s1, s3)
print("更新前s1和s2距离:" + str(distance12))
print("更新前s1和s3距离:" + str(distance13))
# 衰减系数
weight12 = calculate_attenuate_weight(len(s1), len(s2), max_sub12)
weight13 = calculate_attenuate_weight(len(s1), len(s3), max_sub13)
# 更新距离
print("更新后s1和s2距离:" + str(distance12 * weight12))
print("更新后s1和s3距离:" + str(distance13 * weight13))
输出:
更新前s1和s2距离:2.0223748416156684
更新前s1和s3距离:1.794435844492636
更新后s1和s2距离:0.47399410350367227
更新后s1和s3距离:1.6822836042118463
结论:
用新的算法更新后,我们会发现s1和s2距离比s1和s3的距离更加接近了,这就是我们要的结果。
5. 参考
- https://github.com/wannesm/dtaidistance
- 两个字符串的最长子串
- 两个字符串的最长子序列