时间复杂度和空间复杂度简介
算法复杂度分为时间复杂度和空间复杂度。其作用:
时间复杂度是指执行算法所需要的计算工作量;
空间复杂度是指执行这个算法所需要的内存空间。
(算法的复杂性体现在运行该算法时的计算机所需资源的多少上,计算机资源最重要的是时间和空间(即寄存器)资源,因此复杂度分为时间和空间复杂度)。
简单来说,时间复杂度指的是语句执行次数,空间复杂度指的是算法所占的存储空间
一、时间复杂度
1)时间频度:一个算法中的语句执行次数称为语句频度或时间频度。记为T(n)。
2)时间复杂度:
当n不断变化时,时间频度T(n)也会不断变化。一般情况下,算法中基本操作重复执行的次数是问题规模n的某个函数,用T(n)表示,若有某个辅助函数f(n),使得当n趋近于无穷大时,T(n)/f(n)的极限值为不等于零的常数,则称f(n)是T(n)的同数量级函数。记作T(n)=O(f(n)),称O(f(n)) 为算法的渐进时间复杂度,简称时间复杂度。
3)求解算法的时间复杂度的具体步骤:
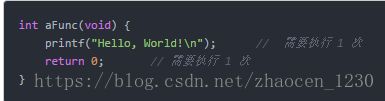
3.1.我们知道常数项对函数的增长速度影响并不大,所以当 T(n) = c,c 为一个常数的时候,我们说这个算法的时间复杂度为 O(1);如果 T(n) 不等于一个常数项时,直接将常数项省略。
比如:
T(n) = 2,所以我们说那个函数(算法)的时间复杂度为 O(1)。
T(n) = n + 29,此时时间复杂度为 O(n)。
3.2.我们知道高次项对于函数的增长速度的影响是最大的。n^3的增长速度是远超n^2的,同时n^2的增长速度是远超n的。同时因为要求的精度不高,所以我们直接忽略低次项。
比如:
T(n) = n^3 + n^2 + 29,此时时间复杂度为 O(n^3)。
3.3.因为函数的阶数对函数的增长速度的影响是最显著的,所以我们忽略与最高阶相乘的常数。
比如:
T(n) = 3n^3,此时时间复杂度为 O(n^3)。
3.4.综合:
如果一个算法的执行次数是 T(n),那么只保留最高次项,同时忽略最高项的系数后得到函数 f(n),此时算法的时间复杂度就是 O(f(n))。
4)部分法则:
4.1.对于一个循环,假设循环体的时间复杂度为 O(n),循环次数为 m,则这个
循环的时间复杂度为 O(n×m)。
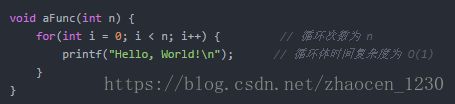
比如:
此时时间复杂度为 O(n × 1),即 O(n)。
4.2.对于多个循环,假设循环体的时间复杂度为 O(n),各个循环的循环次数分别是a, b, c...,则这个循环的时间复杂度为 O(n×a×b×c...)。分析的时候应该由里向外分析这些循环。
比如:
此时时间复杂度为 O(n × n × 1),即 O(n^2)。
4.3.对于顺序执行的语句或者算法,总的时间复杂度等于其中最大的时间复杂度。
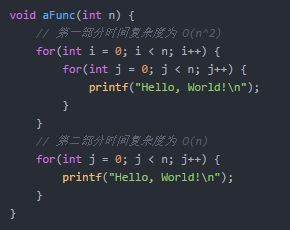
比如:
此时时间复杂度为 max(O(n^2), O(n)),即 O(n^2)。
4.4.对于条件判断语句,总的时间复杂度等于其中 时间复杂度最大的路径 的时间复杂度。
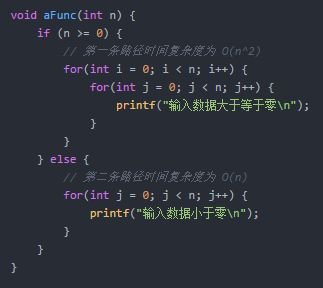
比如:
此时时间复杂度为 max(O(n^2), O(n)),即 O(n^2)。
时间复杂度分析的基本策略是:从内向外分析,从最深层开始分析。如果遇到函数调用,要深入函数进行分析。
5)常见的时间复杂度有:
常数阶O(1)
对数阶O(log2n)
线性阶O(n)
线性对数阶O(nlog2n)
平方阶O(n^2)
立方阶O(n^3)
k次方阶O(n^k)
指数阶O(2^n)
时间复杂度由小到大依次为:
![]()
6)常用排序算法的时间复杂度
|
|
最差时间分析 |
平均时间复杂度 |
稳定度 |
空间复杂度 |
| 冒泡排序 |
O(n^2) |
O(n^2) |
稳定 |
O(1) |
| 快速排序 |
O(n^2) |
O(n*log2n) |
不稳定 |
O(log2n)~O(n) |
| 选择排序 |
O(n^2) |
O(n^2) |
稳定 |
O(1) |
| 二叉树排序 |
O(n^2) |
O(n*log2n) |
不稳定 |
O(n) |
| 插入排序 |
O(n^2) |
O(n^2) |
稳定 |
O(1) |
| 堆排序 |
O(n*log2n) |
O(n*log2n) |
不稳定 |
O(1) |
二、空间复杂度
1)空间复杂度(Space Complexity) :
是对一个算法在运行过程中临时占用存储空间大小的量度,记做 S(n)=O(f(n)) ,其中n为问题的规模。利用算法的空间复杂度,可以对算法的运行所需要的内存空间有个预先估计。
一个算法执行时除了需要存储本身所使用的指令、常数、变量和输入数据外,还需要一些对数据进行操作的工作单元和存储一些计算所需的辅助空间。
2)算法执行时所需的存储空间包括以下两部分:
(1)固定部分。这部分空间的大小与输入/输出的数据的个数、数值无关。主要包括指令空间(即代码空间)、数据空间(常量、简单变量)等所占的空间。这部分属于静态空间。
(2)可变空间,这部分空间的主要包括动态分配的空间,以及递归栈所需的空间等。这部分的空间大小与算法有关。
上方的代码中,当程序调用 reserse() 方法时,要分配的内存空间包括:引用a、引用b、局部变量n、局部变量i
因此 f(n)=4 ,4为常量。所以该算法的空间复杂度 S(n)=O(1)