CRC效验算法
1.CRC简介
CRC即循环冗余效验码:是数据通信领域中最常用的一种查错校验码,其特征是信息字段和校验字段的长度可以任意选定。循环冗余检查(CRC)是一种数据传输检错功能,对数据进行多项式计算,并将得到的结果附在帧的后面,接收设备也执行类似的算法,以保证数据传输的正确性和完整性。
2.从奇偶效验说起
所谓通讯过程的校验是指在通讯数据后加上一些附加信息,通过这些附加信息来判断接收到的数据是否和发送出的数据相同。比如说RS232串行通讯可以设置奇偶校验位,所谓奇偶校验就是在发送的每一个字节后都加上一位,使得每个字节中1的个数为奇数个或偶数个。比如我们要发送的字节是0x1a,二进制表示为0001 1010。
采用奇校验,则在数据后补上个0,数据变为0001 1010 0,数据中1的个数为奇数个(3个)
采用偶校验,则在数据后补上个1,数据变为0001 1010 1,数据中1的个数为偶数个(4个)
接收方通过计算数据中1个数是否满足奇偶性来确定数据是否有错。
奇偶校验的缺点也很明显,首先,它对错误的检测概率大约只有50%。也就是只有一半的错误它能够检测出来。另外,每传输一个字节都要附加一位校验位,对传输效率的影响很大。因此,在高速数据通讯中很少采用奇偶校验。奇偶校验优点也很明显,它很简单,因此可以用硬件来实现,这样可以减少软件的负担。因此,奇偶校验也被广泛的应用着。
奇偶校验就先介绍到这来,之所以从奇偶校验说起,是因为这种校验方式最简单,而且后面将会知道奇偶校验其实就是CRC 校验的一种(CRC-1)。
3.累加和校验
另一种常见的校验方式是累加和校验。所谓累加和校验实现方式有很多种,最常用的一种是在一次通讯数据包的最后加入一个字节的校验数据。这个字节内容为前面数据包中全部数据的忽略进位的按字节累加和。比如下面的例子:
我们要传输的信息为: 6、23、4
加上校验和后的数据包:6、23、4、33
这里 33 为前三个字节的校验和。接收方收到全部数据后对前三个数据进行同样的累加计算,如果累加和与最后一个字节相同的话就认为传输的数据没有错误。
累加和校验由于实现起来非常简单,也被广泛的采用。但是这种校验方式的检错能力也比较一般,对于单字节的校验和大概有1/256 的概率将原本是错误的通讯数据误判为正确数据。之所以这里介绍这种校验,是因为CRC校验在传输数据的形式上与累加和校验是相同的,都可以表示为:通讯数据 校验字节(也可能是多个字节)
4. CRC校验原理
CRC校验原理就是先在要发送的帧后面附加一个数(这个就是用来校验的校验码,但要注意,这里的数也是二进制序列的,下同),生成一个新帧发送给接收端。当然,这个附加的数不是随意的,它要使所生成的新帧能与发送端和接收端共同选定的某个特定数整除(注意,这里不是直接采用二进制除法,而是采用一种称之为“模2除法”)。到达接收端后,再把接收到的新帧除以(同样采用“模2除法”)这个选定的除数。因为在发送端发送数据帧之前就已通过附加一个数,做了“去余”处理(也就已经能整除了),所以结果应该是没有余数。如果有余数,则表明该帧在传输过程中出现了差错。
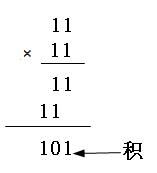
【说明】“模2除法”与“算术除法”类似,但它既不向上位借位,也不比较除数和被除数的相同位数值的大小,只要以相同位数进行相除即可。模2加法运算为:1+1=0,0+1=1,0+0=0,无进位,也无借位;模2减法运算为:1-1=0,0-1=1,1-0=1,0-0=0,也无进位,无借位。相当于二进制中的逻辑异或运算。也就是比较后,两者对应位相同则结果为“0”,不同则结果为“1”。如100101除以1110,结果得到商为11,余数为1,如图5-9左图所示。如11×11=101,如图5-9右图所示。
图5-9 “模2除法”和“模2乘法”示例
具体来说,CRC校验原理就是以下几个步骤:
(1)先选择(可以随机选择,也可按标准选择,具体在后面介绍)一个用于在接收端进行校验时,对接收的帧进行除法运算的除数(是二进制比较特串,通常是以多项方式表示,所以CRC又称多项式编码方法,这个多项式也称之为“生成多项式”)。
(2)看所选定的除数二进制位数(假设为k位),然后在要发送的数据帧(假设为m位)后面加上k-1位“0”,然后以这个加了k-1个“0“的新帧(一共是m+k-1位)以“模2除法”方式除以上面这个除数,所得到的余数(也是二进制的比特串)就是该帧的CRC校验码,也称之为FCS(帧校验序列)。但要注意的是,余数的位数一定要是比除数位数只能少一位,哪怕前面位是0,甚至是全为0(附带好整除时)也都不能省略。
(3)再把这个校验码附加在原数据帧(就是m位的帧,注意不是在后面形成的m+k-1位的帧)后面,构建一个新帧发送到接收端;最后在接收端再把这个新帧以“模2除法”方式除以前面选择的除数,如果没有余数,则表明该帧在传输过程中没出错,否则出现了差错。
通过以上介绍,大家一定可以理解CRC校验的原理,并且不再认为很复杂吧。
从上面可以看出,CRC校验中有两个关键点:一是要预先确定一个发送端和接收端都用来作为除数的二进制比特串(或多项式);二是把原始帧与上面选定的除进行二进制除法运算,计算出FCS。前者可以随机选择,也可按国际上通行的标准选择,但最高位和最低位必须均为“1”,如在IBM的SDLC(同步数据链路控制)规程中使用的CRC-16(也就是这个除数一共是17位)生成多项式g(x)= x16 + x15 + x2 +1(对应二进制比特串为:11000000000000101);而在ISO HDLC(高级数据链路控制)规程、ITU的SDLC、X.25、V.34、V.41、V.42等中使用CCITT-16生成多项式g(x)= x16 + x15 + x5 +1(对应二进制比特串为:11000000000100001)。
5. CRC校验码的计算示例
由以上分析可知,既然除数是随机,或者按标准选定的,所以CRC校验的关键是如何求出余数,也就是校验码(CRC校验码)。
下面以一个例子来具体说明整个过程。现假设选择的CRC生成多项式为G(X) = X4 + X3 + 1,要求出二进制序列10110011的CRC校验码。下面是具体的计算过程:
(1)首先把生成多项式转换成二进制数,由G(X) = X4 + X3 + 1可以知道(,它一共是5位(总位数等于最高位的幂次加1,即4+1=5),然后根据多项式各项的含义(多项式只列出二进制值为1的位,也就是这个二进制的第4位、第3位、第0位的二进制均为1,其它位均为0)很快就可得到它的二进制比特串为11001。
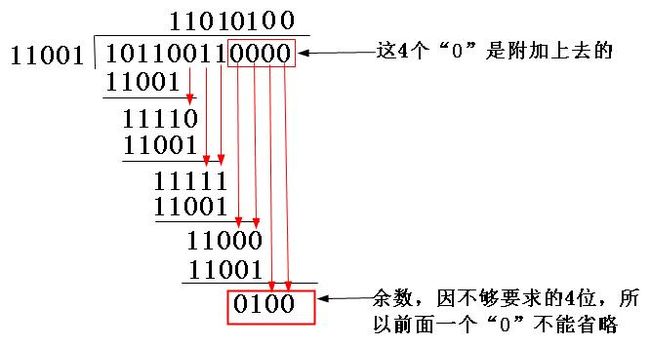
(2)因为生成多项式的位数为5,根据前面的介绍,得知CRC校验码的位数为4(校验码的位数比生成多项式的位数少1)。因为原数据帧10110011,在它后面再加4个0,得到101100110000,然后把这个数以“模2除法”方式除以生成多项式,得到的余数(即CRC码)为0100,如图5-10所示。注意参考前面介绍的“模2除法”运算法则。
图5-10 CRC校验码计算示例
(3)把上步计算得到的CRC校验0100替换原始帧101100110000后面的四个“0”,得到新帧101100110100。再把这个新帧发送到接收端。
(4)当以上新帧到达接收端后,接收端会把这个新帧再用上面选定的除数11001以“模2除法”方式去除,验证余数是否为0,如果为0,则证明该帧数据在传输过程中没有出现差错,否则出现了差错。
通过以上CRC校验原理的剖析和CRC校验码的计算示例的介绍,大家应该对这种看似很复杂的CRC校验原理和计算方法应该比较清楚了。