【ACM】树 小结
树是一种表达层级结构的数据结构,也是实现高效算法与数据结构的基础。
学习之前的基础:数组,循环处理,结构体,递归函数。
树:由结点(node)和连接结点的边(edge)构成。
一、树的相关基本概念:
双亲(父母/前件),子女(孩子/后件),双亲和子女的关系是相对而言的。
兄弟:若几个结点的双亲为同一个结点,则这些结点互称为兄弟。
祖先:将从树根到某一结点K的路径中,K前所经过的所有结点称为K的祖先。
子孙:以某结点K为根的子树中的任意一个结点都称为K的子孙。
结点的度:某一结点拥有的子女的个数。
树的度:树中所有结点的度的最大值。
叶子节点(终端节点):度为0的结点。
分支节点(非终端节点):度不为0的结点。
结点的层次:(有两种不同的说法,有的说根结点所在层次是0,有的说根结点所在层次是1)
树的深度(高度):树中结点的最大层次数。
在一棵树中,除了根节点外,其他任何结点有且仅有一个双亲,有0个或多个子女,他的子女恰巧为其子树的根结点。
二叉树:二叉树是一个由结点构成的有限集合,这个集合或者为空,或者由一个根结点及两棵互不相交的分别称作这个根结点的左子树和右子树的二叉树组成。
有序树:若树中任意结点的子树均看成是从左到右有次序的,不能随意交换,则称该树是有序树。
------------------------------------------------------------------------------------------
二叉树不是一般树形结构的特殊形式,它们是两种不同的数据结构
区别:
1、二叉树中每一个非空结点最多只有两个子女,而一般的树形结构中每个非空结点可以有0到多个结点。
2、二叉树中结点的子树要区分左子树和右子树,即使在结点只有一颗子树的情况下,也要明确指出是左子树还是右子树。
------------------------------------------------------------------------------------------
现学现用
1、Rooted Trees(有根树的表达)
https://vjudge.net/problem/Aizu-ALDS1_7_A
这题是对一棵树结点的相关信息进行输出,输入数据完成,则是一棵确定的树
关键是用什么方法存储一个结点的信息(结点序号,双亲结点的序号,深度,结点类型,所有子女序号)
这里使用的是:左子右兄弟表示法
该方法包含以下信息:1、结点的父结点。2、结点最左侧子结点。3、结点右侧紧邻的兄弟结点。
//左子右兄弟表示法
typedef struct
{
int parent;
int left;
int right;
}Node;#include
#include
#include
using namespace std;
const int maxn = 100000+10;
//左子右兄弟表示法
typedef struct
{
int parent;
int left;
int right;
}Node;
Node T[maxn];
int n;
int getdepth(int u)
{
int d=0;
while(T[u].parent!=-1)
{
u=T[u].parent;
d++;
}
return d;
}
void print(int u)
{
int i,c;
cout << "node "<> id >> k;
for(j=0;j> c;
if(j==0)
T[id].left=c;
else
T[l].right=c;
l=c;
T[c].parent=id;
}
}
for(i=0;i 2、Binary Tree(二叉树的表达)
这个题是对二叉树的相关信息进行输出,结点的双亲的序号,它的兄弟结点,该结点的度,该结点的深度(层次数),该结点高(该结点往下,到叶子节点的最长路径),该结点的类型
与上一题相比,该结点的度是小于等于2的,及最多有两个子女,比上一题的树可能有0到多个子女方便处理一些。
#include
using namespace std;
typedef struct
{
int p,l,r;
}node;
node T[100000+5];
int getdepth(int u)
{
//到根结点的距离
int d= 0;
while(T[u].p!=-1)
{
u=T[u].p;
d++;
}
return d;
}
int sibling(int u)
{
if(T[u].p==-1)
return -1;
if(T[T[u].p].l!=u && T[T[u].p].l!=-1)
return T[T[u].p].l;
if(T[T[u].p].r!=u && T[T[u].p].r!=-1)
return T[T[u].p].r;
return -1;
}
int getdegree(int u)
{
int d=0;
if(T[u].l!=-1)
d++;
if(T[u].r!=-1)
d++;
return d;
}
int getheight(int u)
{
int a=0,b=0;
if(T[u].l!=-1)
a = getheight(T[u].l)+1;
if(T[u].r!=-1)
b = getheight(T[u].r)+1;
return (a>b)?a:b;
}
void print(int u)
{
cout << "node "<>N;
for(i=0;i> id>> l >> r;
T[id].l=l;
T[id].r=r;
if(l!=-1)
T[l].p=id;
if(r!=-1)
T[r].p=id;
}
for(int i=0;i 二、树的遍历
树的常用遍历:
(1)树的前序遍历。首先访问根结点,再从左到右依次按前序遍历的方式访问根结点的每一棵子树。
(2)树的后序遍历。首先从左到右依次按后序遍历的方式访问根结点的每一棵子树,然后再访问根结点。
(3)树的层次遍历。首先访问第一层上的根结点,然后从左到右依次访问第二层上的所有结点,再以同样的方式访问第三层上所有结点......最后访问树中最低一层的所有结点。
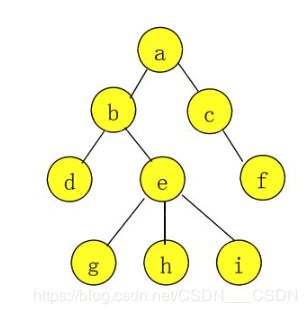
前序遍历:a b c e f h i g d
后序遍历:b e h i f g c d a
层次遍历:a b c d e f g h i
二叉树的遍历
是指按照一定的顺序对二叉树中的每一个结点均访问一次,且仅访问一次。
按照根结点访问位置的不同,通常把二叉树的遍历分为3种:前序遍历,中序遍历,后序遍历
(1)前序遍历:(根,左,右)
首先访问根结点;
然后按照前序遍历的方式访问根结点的左子树;
再按照前序遍历的方式访问根结点的右子树。
(2)中序遍历(左,根,右)
(3)后序遍历(左,右,根)
前序遍历:a b d e f g c
中序遍历:d e b g f a c
后序遍历:e d g f b c a
现学现用:
typedef struct
{
int parent;
int left;
int right;
}Node;1、Tree Walk
https://vjudge.net/problem/Aizu-ALDS1_7_C
输出三种遍历结果,注意输出格式
采用的是递归地遍历二叉树
#include
using namespace std;
const int maxn = 50;
typedef struct
{
int parent;
int left;
int right;
}Node;
Node T[maxn];
int n;
void preorder(int u)
{
if(u==-1)
return ;
cout << " "<> n;
for(i=0;i> id >> lchild >> rchild;
T[id].left=lchild;
T[id].right=rchild;
if(rchild!=-1)
T[rchild].parent=id;
if(lchild!=-1)
T[lchild].parent=id;
}
int root;
for(i=0;i 下面是非递归地遍历二叉树
需要用到栈stack
前序遍历(根,左,右)
对于一棵二叉树t,如果t非空,访问完t的根结点值后,就应该进入t的左子树,但此时必须将t保存起来,以便访问完其左子树后,进入其右子树访问,即应该在t处设置一个回溯点,并将该回溯点进栈保存。
void preorder(int u)
{
stack s;
while((u!=-1) || s.empty()!=1)
{
if(u!=-1)
{
cout << " " << u;
s.push(u);
u=T[u].left;
}
else
{
u=s.top();
s.pop();
u=T[u].right;
}
}
} 中序遍历:(左,根,右)
对于一棵树t,如果t非空,首先应将进入t的左子树访问,此时由于t的根结点即右子树尚未访问,因此必须将t保存起来放入栈中,以便访问完其左子树后,从栈中取出t,进行其根结点及右子树的访问。
void inorder(int u)
{
stack s;
while((u!=-1)||(s.empty()!=1))
{
if(u!=-1)
{
s.push(u);
u=T[u].left;
}
else
{
u=s.top();
cout << " "< 后序遍历(左,右,根)
对于一棵树t,首先应该进入t的左子树访问,此时由于t的右子树及根结点尚未访问,因此必须将t保存起来放入栈中,以便访问完其左子树后,从栈种取出t,
void postorder(int u)
{
stack S,s;//s用来标记,S用来暂存数据
while((u!=-1)||(S.empty()!=1))
{
if(u!=-1)
{
S.push(u);
s.push(0);
u=T[u].left;
}
else
{
if(s.top()==1)
{
s.pop();
u=S.top();
S.pop();
cout << " "< 三、树遍历的应用——树的重建
分别输入二叉树的前序遍历和中序遍历,输出相应的后序遍历
分别输入二叉树的中序遍历和后序遍历,输出相应的前序遍历
无法通过前序遍历和后序遍历求的中序遍历:前序和后序在本质上都是将父节点与子结点进行分离,但并没有指明左子树和右子树的能力,因此得到这两个序列只能明确父子关系,而不能确定一个二叉树。
现学现用
1、Binary Tree Traversals(知道前序,中序求后序)
前序遍历 (根左右):1 2 4 7 3 5 8 9 6
中序遍历(左根右):4 7 2 1 8 5 9 3 6
https://vjudge.net/problem/HDU-1710
核心代码!!!!(递归的思想)
void fun(int l,int r)
{
//distance函数返回的是两迭代器之间的距离
if(l>=r) return ;
int root=pre[pos++];
int m = distance(in.begin(),find(in.begin(),in.end(),root));
fun(l,m);
fun(m+1,r);
post.push_back(root);
}测试样例:
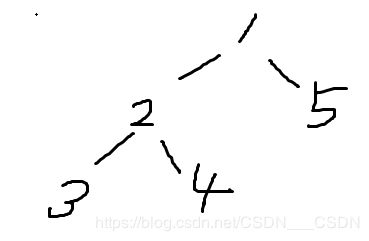
5
1 2 3 4 5(前序遍历)
3 2 4 1 5(中序遍历)设前序遍历的当前结点c,c在中序遍历中的位置是m,m的左侧就是c的左子树,右侧就是c的右子树,然后同理递归。
例如
当前的结点为1,其在中序遍历中的位置是 3 2 4 [1] 5,那么当前树的根就是1,左右子树就是 3 2 4 和 5。接下来在3 2 4 组成的树中,前序遍历的下一个结点是2是根,3 [2] 4,3和4是两个子树。以此类推...
#include
#include
#include
#include
#include
#include
using namespace std;
vector pre,in,post;
int pos,n;
void fun(int l,int r)
{
//distance函数返回的是两迭代器之间的距离
if(l>=r) return ;
int root=pre[pos++];
int m = distance(in.begin(),find(in.begin(),in.end(),root));
fun(l,m);
fun(m+1,r);
post.push_back(root);
}
void solve()
{
int i;
pos=0;
fun(0,pre.size());
for(i=0;i> x;
pre.push_back(x);
}
for(i=0;i> x;
in.push_back(x);
}
solve();
}
return 0;
} 2、Tree Recovery(知道前序、中序求后序)
https://vjudge.net/problem/POJ-2255
#include
#include
#include
#include
#include
#include
using namespace std;
vector pre,in,post;
int pos,n;
void fun(int l,int r)
{
if(l>=r)
return ;
char root = pre[pos++];
int m = distance(in.begin(),find(in.begin(),in.end(),root));
fun(l,m);
fun(m+1,r);
post.push_back(root);
}
void solve()
{
pos = 0;
fun(0,pre.size());
for(int i=0;i 3、756-重建二叉树(知道后序和中序,求前序)
http://nyoj.top/problem/756
这个题目和之前的两个题目有一点不同,思想都是一样的,但是后序遍历是左右根,所以,需要不断地往前推,而且在往前推的过程中,先得到的是右子树上的根结点,再次是左子树上的,所以存入pre这个vector中的顺序是“右左根”,所以在输出的时候要倒序输出。
#include
#include
#include
#include
#include
#include
using namespace std;
vector pre,in,post;
int pos,n;
char s1[1000],s2[1000];
void fun(int l,int r)
{
if(l>=r)
return ;
char root = post[pos--];
int m = distance(in.begin(),find(in.begin(),in.end(),root));
fun(m+1,r);
fun(l,m);
pre.push_back(root);
}
void solve()
{
pos = strlen(s1)-1;
fun(0,in.size());
for(int i=in.size()-1;i>=0;i--)
{
cout << pre[i];
}
cout << endl;
}
int main ()
{
//知道后序和中序遍历,求前序遍历
int i;
while(scanf("%s %s",s1,s2)!=EOF)
{
i=0;
pre.clear();
in.clear();
post.clear();
while(s1[i])
{
post.push_back(s1[i]);
i++;
}
i=0;
while(s2[i])
{
in.push_back(s2[i]);
i++;
}
solve();
}
return 0;
}