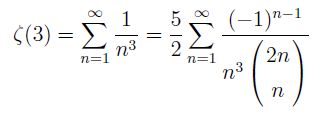Zeta函数与超越不变量
数学研究的对象在一般的感觉里是比较抽象的, 虽然它也有很实际的一面。在数论探讨的是数,在数学里它是最古老的一支。但是, 它仍有许多没有解决的难题。我今天的题目是Zeta 函数与超越不变量, 就涉及了一些这样的问题。
我们先从数开始。所谓的数, 在数学里是指自然数、整数、有理数, 然后是实数。所以, 通常在中学的教科书里, 画有一个数线,先描上原点O,然后向右等距画出所有自然数的点, 向左对称地点出负整数点。再以等分点对应有理数。最后所有的实数点就会填满整条数线。
我们用N 代表所有自然数集合, Z 代表所有整数的集合, Q 代表所有有理数的集合, R 代表所有实数集合。其包含关系如下:
N ⊂Z ⊂Q ⊂R
数论里面的难题往往可以很简洁地描述。一个例子是所谓的费玛(Pierre de Fermat, 1601-1665) 问题。方程式
Xn+ Y n= Zn, XY Z≠0, n > 2
没有整数解。这个问题经过三个半世纪, 终于在1994年被Princeton 大学的A.Wiles 教授证明出来。这个问题的解决, 被认为是本世纪在数学(至少是纯数学) 里面最大的进展。
数论的特质之一就是你可以写下很多这样看起来很简单, 中学生都可以了解的问题,解答起来却是非常困难。对数论有兴趣的人,往住会花很多的时间, 总其一生的精力, 试图去证明或解决这样的问题。
实数里有一个很特别的数,
π=3.14159265358979323846264338…。
它不是有理数, 甚至不是任何整系数方程式的根, 这种数叫做超越数。π在小学数学里就开始教了, 但是它其实是一个不容易的观念。我们说π是一个不变量, 不论你画那一个圆, 圆周长和直径的比例是不变的, 这个比例就是π。如果你实际去算的话, 就会一直不断地写下小数点后面的数字来。然后你就会发现, 这些数目字其实是非常非常不规则。
小学生碰到π的时候, 通常有一个疑惑, 就是π到底是多少。你如果只写下有限个位数,其实并不正确。正确的方式是要一直写下去,小数点右边不能停下来。写得愈多位数就愈接近真正的π。既然这些小数点后面的数目字出现得杂乱无章, 这样子的一个数, 你怎么去了解它呢?
所谓π是超越数的意思是说, 它不满足任何一个代数方程式:
a0+a1π+…+anπn= 0, 其中ai是整数。
这是Lindemann 在1882年证明的事。当时证明了这个定理被认为是十九世纪最重要的数学成就之一。
我们为什么要去证明「π不会是任何一个整系数代数方程式的根」这样的事呢?假如它满足了某一个代数方程式, 找到这个方程式就能够提供我们有关它的重要的信息,要了解它就容易多了。所以为了要真正了解这一个很实际的数, 就必须先确定它是否满足某代数方程式。如果一个数满足某个整系数代数方程式, 就称为代数数。否则就称之为超越数。但是在数学上不能因为你找不到这样一个方程式就说它没有。因为可能是有而你还没找到。所以唯一能够说它没有的方式,就是你必须去证明。真正从逻辑上去证明,π不满足任何代数方程式。这是很困难的事, 是数学家经历了两百年才证明出来的一件事情。
一个有理数如果以十进制数展开, 写出的数目字就会相当规则。也许某位数以后都是0, 也就是只有有限的位数。不然的话, 它所出现的数目字就会是循环的, 也就是说往小数点右方继续展开下去会有周期的现象。π是一个超越数, 就表示在它的小数展开里, 数目字出现得相当复杂、相当不规则。一个基本的问题是: 我们如何掌握或描述一个数的「复杂程度」。这个问题到今天还没有完全解决。我们仍然没有一个满意的方法, 把所有的数按复杂程度去分类。像π这个数, 它不满足任何代数方程式, 你只能一步一步的去接近它, 近似它。这其实已经不是容易的事了。
1950 年代计算机刚诞生在Princeton 时, 数学家就用计算机来计算π, 可以近似到小数点之后两仟位。现在用最新的超级计算机, 可以算到几十亿位。从两仟位到几十亿位, 这中间不只是计算机硬件的进步, 计算方法更有大幅的改进。计算方法的改进就是数学, 也就是说你必须找到更好的数学方法去作数值近似。从古希腊、祖冲之、牛顿到现代, 数学家仍持续不断的在找寻更好的数学方法去近似π。
从π再回到最基本的数: 整数。在整数中间作除法, 就引进了有理数。令Q 是所有的有理数所成的集合, 在这集合里就可以做加、减、乘、除四则运算。这样的一个结构,我们叫做域。所有实数R 也构成一个体, 比Q 更大的域。复数C 又构成一个更大的域。
为了要深入探讨像Q 这样一个域, 数学家引进了特别的工具来辅助研究。Zeta函数就是这样的一种工具
ζ(s) =∑∞n=1(1/ns) , Re(s) > 1.
这是上世纪中Riemann 所写下的Riemann Zeta 函数, 是一个无穷级数。其中s表示一个复数变量, 在复数平面上跑, 原先的数轴是复数平面上的x-轴, y-轴表示虚数轴,其上的点对应所谓的纯虚数。这个Zeta 函数级数里的每一项是1/ns的形式, n 是正整数。
引进这种特殊的函数, 似乎是很唐突的事, 不知从何处冒出来, 但是这一步对于整个数学的发展却是相当关键的。在Riemann之前, 已经有很多迹象出现。早他一百年,Euler 就发现了以下的公式, 对于偶数m
ζ(m) =∑∞n=0(1/nm) =(−(2π√−1)m/2m!)Bm
把偶数m 代进s, 就是Zeta 函数在m 的取值, 左边的Bm 是一个有理数的数列, 称为Bernoulli 数, 它们可以很容易的从指数函数ez的幂级数展开算出来:
z/(ez− 1)=∑∞m=0Bm(zm/m!)
B0 = 1,B1 = −1/2,B2 = 1/6,B3 = 0,B4 = 1/30,B5 = 0,…
Euler发现的这个公式到底有什么意思呢? 首先, 这个式子是出人意之外的, Zeta函数和超越不变量π分别出现在等式的两边。π原来是从圆周长来的, 因而表示圆和Zeta 函数是有关联的, 也表示指数函数和Zeta 函数是有关联的。π在数学里之所以非常重要, 就是因为它会在许多令人意外的关键场合很漂亮地出现。Euler这个式子背后其实隐藏着许多丰富的现象。
由Euler 的公式我们知道ζ(2) 是π2乘上一个特别的有理数, ζ(4) 是π4 乘上一特别的有理数, 等等。因此我们完全清楚了ζ(2),ζ(4),…, 因为π是超越数, 这些函数值当然也是超越数。
如果令变量s 趋近于1,ζ(s) 的值会趋近无穷大, 但是只要复数s 的实部大于1, 级数和都会收敛, 除了2, 4, 6,…等偶数点的取值, 当然也可以让Zeta 函数在3, 5, 7, …等大于1 的奇数上取值, 可是这就发生问题了, 不仅Euler 不知道ζ(3), ζ(5), …, 直到今天我们仍然几乎什么都不知道。唯一知道的事是1978年法国数学家R. Apery 证明出ζ(3) 不是有理数。连ζ(5) 是不是有理数都还不知道。
Apery 能够证明ζ(3) 不是有理数是因
为他得到另一个算式
等式中间的级数及右边的级数各给了一个方式去近似ζ(3), 所不同的是以右边的级数去近似速度上会快很多。能够多快的去逼近一个实数是一个关键, 涉及了一个基本现象:如果能写下一个数列“不太慢”的去近似一个数而不碰到那个数, 那个数就必然不是有理数。原来用来定义ζ(m) 的级数, 缺点就是收敛的太慢, 取近似值时速度也太慢。当初Euler 研究他的公式就是先去作数值计算ζ(2), ζ(4), …, 他发现级数走得太慢, 因此想找出更好的线索。经过几年努力他猜到了公式, 然后又经过十余年才证明出他的公式。
对于一个我们有兴趣的数, 像π, 很重要的问题是能找到多快的方法去近似它。前面谈过近几十年来π的近似值计算, 所以能算出几十亿位除了计算机进步外, 就是因为数学家还一直在努力找更好更快的方法去近似π。
这里所涉及的深奥数学, 不只关系到一个数是否是有理数, 也关系到一个数是否是超越数。早在上世纪Liouville 就已发现, 如果我们能够足够快的去近似一个数而不碰到那个数, 则那个数就应该是超越数。问题是这儿所谓速度足够快到底要多快, 须要精确的研究。
速度是跟用以近似的有理数的分母以及误差相关。这个问题经过百年研究到1956年伦敦大学的Roth 才完全解决。他的工作随后就获得了国际数学会的Fields 奖。
如同自然界的许多现象, 数学现象往往也可以推得很广, 可以有很多的变化, 并以很多不的形式呈现。与上述求近似值类似的一个现象是去考虑空间。数与空间都是数学里研究的基本对象。周炜良院士有一个很有名的定理, 是说在复数射影空间里, 解析子空间一定也是代数子空间。代数子空间就好比是代数数, 是可以由一组多项式来描述的。解析子空间就像是实数, 放在射影空间中受到了限制, 就必须是代数子空间。
根据陈省身院士的说法, 周院士的这个定理,当初部分的灵感就是来自「有理数逼近实数时, 如果速度受限, 能被逼近的数就必须是代数数这个事实」。陈院士与周院士年轻时曾经一起在德国做研究, 知晓这个周定理与数论中有理数近似代数数的关联典故。陈院士在美国数学会纪念周院士的文章里, 还特别写出了这个故事。
再回到Zeta 函数。我们可以把Rimann Zeta 函数看成定义在复数平面上的解析函数。原本的定义级数只有在s 的实部大于1才收敛, 但是借着所谓解析延拓, 我们可以让它生长在整个复数平面上。然后, 这个函数就会有一种对称性, 并满足一个函数方程式。
Λ(s) =π−s/2Γ(s/2)ζ(s),
Λ(s) =Λ(1 − s).
这里对称性是说函数Λ(s) 在s 与1-s 的取值完全一样。在实数s = 1/2 作垂线, 把复数平面分为两半,则Λ(s) 在左右两个半平面是完全对称的。回到Zeta 函数, 这个对称性告诉了我们Zeta 函数在负整数点的取值。在负偶数, Zeta 函数值是0; 在负奇数Zeta 函数的取值是把Euler 公式中π的乘幂扔掉后所剩下的有理数。
由于Zeta 函数很对称, 它的零根也应是对称的。这个对称性就产生了一个数学上最重要的问题, Riemann猜想: Zeta 函数所有的零根, 除了负偶数外, 都正好落在实部等于1/2 的x-轴垂直线上。这个Riemann猜想可以导出很多有用的结果, 从有关质数的分布到理论计算器科学上的重要结果。很多数学家甚至认为, 继Fermat 问题解决之后, Riemann 猜想是廿一世纪数学研究致力的最大目标。
RiemannZeta 函数既然是很重要而牵连甚广的函数, 与它性质相近的函数当然也是很有意思的。于是数学家考虑广义的Zeta函数, 这些函数都生长在复数平面上, 都有对称性而满足适当的函数方程式。对每一个这种Zeta 函数也都可以作Riemann 猜想, 而它们在整数点的取值也应该都是很微妙的不变量。虽然对任何一个这种Zeta 函数我们并没有更多知识, 但是考虑这些函数仍然可以发挥很大的作用。Wiles 解决Fermat 问题时就用到广义的Zeta 函数。
解决Fermat 问题, 要用反证法: 假定有解, 然后找出矛盾。首先假定有非零整数a, b, c 使
al+ bl= cl
其中l 是固定奇质数。依Frey 的建议, 再考虑方程式
y2= x(x − al)(x + bl)
对任何与abc 互质的质数p, 考虑二元同余方程式
y2= x(x − al)(x + bl) (mod p)
解出同余解的个数为p − ap。然后从数列{ap}p依一定方式扩充到一个数列{an}∞n=1,再作函数
Sabc(s) =∑∞n=1an/ns
这个Zeta 函数也有一种对称性,它满足函数方程式:
Λ(s) =(√N/2π)sΓ(s)Sabc(s),
Λ(s) = ±Λ(2 − s),
其中N 是一个与a, b, c 有关的正整数。从这个Sabc(s), 根据Ribet 的理论, 可以跳到另一个Zeta 函数, 满足同型的函数方程式。
但是N 可以降下来, 一直到降到2为止。然后从这种复变函数理论里, 可以导出满足上述方程式的这种Zeta 函数只有零函数。因此这种函数不可能存在。因而, 一开始始作俑者的Fermat 方程式整数解a, b, c 必定原来就是不能存在的!
Zeta 函数ζabc(s) 在这儿是作为一个相当复杂的工具。有点像在中学几何里面画参考线, 要走很远的路, 写很长的论文, 证明很多细节, 最后才导出矛盾。
有另外一种Zeta函数, 来自所谓的有限域。域是一个集合, 对里面的元素你可以做加、减、乘、除。这个集合可以只有有限个元素,就叫做有限域。一个有限域的元素个数一定是一个质数p 的乘幂q。这个时候, 这个域就是所谓的特征p 的域,里面任何一个元素把它自己加了p 次以后就变成零了。也就是说, 在它的世界里面你是走不远的, 你走了p 步就一定走回原点。这样的一个世界虽然怪, 其实是有用的。在现代理论计算器科学里面, 很多地方就是可以用到有限域, 例如涉及网络安全的密码学。
一个有限域只是一个有限的集合, 看起来很简单。我们把这个域的元素来做系数, 然后再加上一个变元t。这样以加、减、乘运算得到集合称为多项式环A = Fq[t]。里面的元素就是多项式, 系数在有限体里:
∑ni=0citi, i ∈Fq。这样子写多项式的时候,可以把它看成像整数的十进制展开, 系数就是一种digits。这些多项式运算起来就像原来的整数, 虽然走了p 步就一定走回原点。在原来的数的世界里面, 当然没有这样的性质。
可是另外一方面, 它的加乘等很多性质是跟整数很像的。所以这些多项式其实是一种不同世界里的整数。
从整数做除法可以得到分数。从多项式做除法也可以得到有理式, 或叫它有理函数。这些有理函数所成集合可以做加减乘除, 因此构成一个域, 就是所谓的函数体K =Fq(t), 相当于原来的有理数域。我们把有理数域放到实数域里填充成一条数线, 在这里也可以把函数域放入一条函数线。当然这里的线已经不是通常的直线。它的点对应的是一种幂级数, 以1/t为变元的幂级数。写成
cntn+…+c0+c−1/t+c−2/t2+…, ci∈Fq。
它的左半边为多项式, i 走到某个n 为止, 右半边的级数, i 从−1,−2,−3,−4,…, 可以一直走下去。这个无穷系数序列ci, 就像一个实数的无穷多个digits。所有这些幂级数构成一个域Fq(( 1/t ))。
在九十年前, 美国Carlitz 引进了下面的zeta 函数, 对正整数m:
ζc(m) =∑a∈A a monic 1/am∈Fq((1/t))
如同作Riemann Zeta 函数, 把多项式当成整数, 然后把它倒过来取它的乘幂。原来祇取正整数做, 现在就取那些首项系数是1的多项式来做级数的项。整个无穷级数加起来之后,它的极限值仍然会在体Fq((1/t)) 里。
这些值ζc(m)是很有意思的。Carlitz发现了以下的现象: 当m 是q−1 的倍数的时候, 可以得到一个公式, 很像Euler 原来对Riemann Zeta 函数所得到的公式
ζc(m)=π~mB~m/Γm+1
其中Γm 是多项式的阶乘, 定义是先定D0=1,Di= (t^qi− t^qi−1)…(t^qi− t) 若i ≥ 1,然后写下m 的q 进位展开∑∞i=0miqi, 再定Γm+1 =∏∞i=0Dimi。Bernoulli-Carlitz数B~m 是有理函数的序列, 它的定义是从Taylor 展开式得来:
z/expc(z)=∑∞n=0B~n(zn/Γn+1)
其中expc(z)是Carlitz 指数函数expc(z) =∑∞i=0Zqi /Di。这个Carlitz 指数函数也是一种周期函数,π~就是它的基本的期, 是一个像圆周率乘上2√−1 那样的不变量。
公式里有一个π~、有理函数B~m、以及阶乘多项式Γm+1。在原来Euler 的公式里面, m 必须是偶数, 因为整数里面只有两种符号(sign):+1,−1。在有限域Fq 的世界里面却有q − 1 种符号, 有限域里每一个非零元素都对应一个符号。公式要成立m 就必须是符号个数的倍数。所以在Euler 的公式里m 是2的倍数, 而在Carlitz 的公式里m 是q − 1 的倍数。
就像圆周率π, π~也应是所谓的超越数。也就是说, 它不会满足任何一个多项方程式:
a0+ a0π~+…+ anπ~n= 0
方程式的系数ai 是在多项式环A 里。因为这里的A, 就扮演了原来的整数集合的角色。
π~的超越性是Carlitz 的学生Wade 证明的。把π~除以tq−t 的q −1 次根就得到一个Fq(( 1/t )) 里的超越数。这里的超越数表面上看起来够奇怪。但是从另一角度来看, 却有更好的性质。
五十年前, 法国数学家Christol-Cobham 发现: 在Fq(( 1/t ))这个世界里面, 数的复杂性可以有比较好的描述。譬如:
cntn+…+c0+c−1/t+c−2/t2+…, ci∈Fq,
它是否满足代数方程式的充要条件正好是看系数序列ci 是不是可以由一个有限Automata 来辨识。有限Automata 其实就是最简单的计算机, 只有有限个state。前面说过到今天我们仍然没有一个满意的方法, 把通常的数按复杂程度去分类。但是对Fq(( 1/t ))里的数的复杂程度, 却可以翻译成计算机科学的话去描述。计算机科学中不同的计算复杂阶层, 从有限Automata 到Turing machine正好可以用来呈现Fq(( 1/t ))里的数的复杂程度。
回到我们研究的问题上。对于Carlitz的这些zeta 值ζC(m), 我们想要了解。这里有一个特别有意思的现象, q 可以是任何质数的乘幂, 最小可以是2。当q 是2的时候,q −1 就是1。因而Fq(( 1/t ))的世界是一个没有sign 的世界。每一个数乘上−1 都是自己, −1 等于1。在这个没有sign 的世界, 就有一个简单的结论, 任何整数都是q − 1 的倍数。于是Carlitz 公式清楚的告诉了我们所有的ζC(m)。一般情形下q 不是2, 当m不是q−1 的倍数的时候, 我们仍然有兴趣这些zeta 值。就像原来古典数论里Euler 的问题, 要了解ζ(3), ζ(5), …。
在1991年, Anderson-Thakur解决了上述的的问题。对于任意q 我们都得到ζC(m) 的完整了解。这里m 只要是正整数, 即使m 不是q−1 的倍数, 我们也能清楚的知道ζC(m), 并且证明它是超越数。不只是如此, 我们更知道, 在m 不是q−1 的倍数的时候, ζC(m) 和π~m之间的比例一定也是超越数。这是一个出乎意料之外的进展。在Fq(( 1/t )) 这个比较怪的世界里面, Euler的问题竟然完全解决了。这是三百年来古典数论想做而不能够做到的事情。很多数学家曾经
问过以下的问题: 当m 是奇数时,ζ(m) 和πm 之间的比例是否是有理数? 因为当m 是偶数时Euler 的公式说ζ(m) 和πm之间的比例确是有理数。我们得到的结果显示答案可能是否定的。不仅ζ(m) 和πm之间的比例不应该是有理数, 它甚至不可能是代数数。当然, 我们的证明是在一个不同的世界, 对不同种的zeta 值。因此逻辑上并没有回答上面的问题, 只是给了一点启示。也就是说, 合理的猜想应是: Riemann Zeta 函数在整数点的取值会产生无穷多个超越不变量。π是里面最简单的一个, 其它ζ(3), ζ(5),…, 会得到一串无穷多个代数上不相关的超越不变量。
有一次在Princeton, Fields 奖得主Bombieri 与Deligne谈起这个Zeta函数值的工作。他们认为: 证明当m 是奇数时ζC(m) 和π~m之间的比例也是超越数, 是极漂亮的事。这两个值本应该是没有关系的,但是在过去, 没有人能举出任何道理来说明它们没有关系。我们所做的工作, 让他们可以完全相信这个Riemann Zeta 函数值的问题有朝一日也可以解决。
π来自于圆。π~也来自一种对称结构。在数学的术语里, 对称结构其实是有一个群在作用。例如圆, 你可以让整数加法群作用, 也就是说, 圆可以转整数倍的角度。因此, 把这个观念推广就可以以所谓的交换代数群来取代圆的观念。从这几句话, 数学家大概用了百年的时间去发展。现代的高等数论的核心就在这里。我们可以想象π~来自于函数域的圆,是不同世界里另一种圆。这种圆上不是整数在作用, 而是多项式在作用。从古典的圆推广到多项式在作用的对称结构更是走了一大步,经过Carlitz 引进Carlitz 模到Drinfield在六十多年前所发展出的Drinfield 模理论。这一大步对于数论以及算术几何有很大的影响, 因此Drinfield 也是Fields 奖得主。
要去证明π或π~是超越数, 对称结构扮演相当关键的角色。所谓指数函数, 就是用来参数化圆或Carlitz 模的函数, 它们可以把整数或多项式的非线性作用转化为线性作用。指数函数总是周期函数, 2π√−1 或π~就是它们的基本周期。我们能证明π或π~是超越数, 也就是因为它们是有理对称结构的周期。
为什么能证明当m 是奇数时ζC(m) 和π~m之间的比例也是超越数, 则是因为它们是不同的有理对称结构的周期。这里的一个灵感来自Hilbert 第七问题。
在1900 年的时候, 德国领导数学家Hilbert 在世界数学大会上曾经给了一个演讲, 列出了二十三个二十世纪的主要数学问题。其中第七问题是说: 如果a≠ 0, 1 与b 都是代数数, 而b 不是有理数, ab是否是超越数? 这个当时被认为极困难的问题, 在1934年的时候就被俄国Gelfond 证明了。他发现: 任何两个代数数的对数, 如果他们的比例不是有理数, 就必须是超越数。这些比例不可能是非有理的代数数。譬如说, 它不可能是√2,√3,…, 不可能满足任何代数方程式而不是有理数。它祇能满足一次的方程式, 或者任何代数方程式都不满足。在30年代很多人就猜想这个基本的现象可以推广到不只是两个对数, 而是任意有限个代数数的对数。从这个猜想可以导出很多的重要结果。因此1966年Baker 解决它之后就得到Fields 奖。
这个有关代数数对数的重要基本现象,即使走到有限体上函数域的不同世界仍然存在。布于函数域的对称结构Drinfield 模有它的指数函数, 也有它的对数函数, 包括高维的对数向量。周期则可以看成广义的代数数对数。这中间, 虽然表面上看起来是完全不同的世界, 但是追根究底到了关键的地方, 是有异曲同工之妙。Anderson-Thakur 证明了ζC(m) 是某种m 维Drinfield 模上代数向量的对数。当m 是奇数时,ζC(m) 和π~m之间的比例不是有理函数,所以它是超越数。在古典数的世界里, 我们猜想Riemann Zeta 函数值
ζ(m) 和πm 也是某种对称结构的代数向量的对数, 这种对称结构称为Motives。可是因为了解不够, 目前无法证明任何事。
一旦走进函数域的世界, 就可以做相当多事情。我只能举出其中一小部份。在函数域的世界, 不只是可以从直线的有理函数域出发, 其实还可以从任意曲线的函数域出发。所以我们可以有一整套全新的现象衍生出来。
∑编辑 | Gemini
来源 | 数哲三叔
算法数学之美微信公众号欢迎赐稿
稿件涉及数学、物理、算法、计算机、编程等相关领域,经采用我们将奉上稿酬。
投稿邮箱:[email protected]