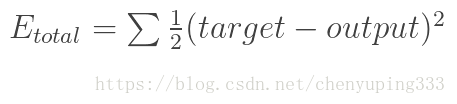神经网络：ResNet 论文学习总结（一）

引言

对于深度学习初学者，对网络结构总是存在模糊的认识，不能确切的把握结构的要义。在学习探索过程中，对网络结构算法的有效性和准确度没有很高的要求，经常不考虑时间成本和效率因素，但在工作和实际场景应用时，存在着各种硬性的要求，在较短或者很短的时间内训练出较好或者符合应用场景最低要求网络模型。

对于 ResNet 网络结构，本人由于没有深刻的学习和相关的总结，在实习和学习过程中总是碰壁。非常感谢实习的主管，给予我很大的帮助。本文是本人阅读 ResNet 论文和结合实习经历之后的简单总结，共两篇。第一篇（即本篇）主要讲 ResNet，第二篇主要讲对 ResNet 网络结构的优化。

ResNet 网络简介

《Deep Residual Learning for Image Recognition》论文由微软研究院的kaiming He等4名华人提出，通过使用Residual Unit成功训练152层深的神经网络，在ILSVRC 2015比赛中获得了冠军，取得3.57%的top5错误率，同时参数量却比VGGNet低，效果非常突出。ResNet的结构可以极快地加速超深神经网络的训练，模型的准确率也有非常大的提升。论文链接

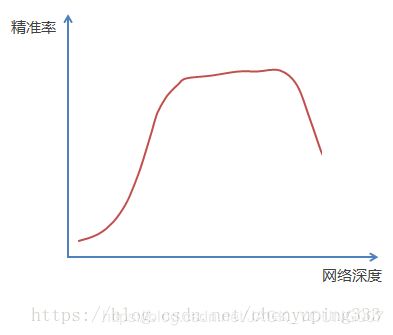
ResNet 主要解决的问题是：在不断增加神经网络的深度时，会出现一个Degradation（退化）的问题，即准确率会先上升然后达到饱和，再持续增加深度则会导致准确率下降。这并不是过拟合的问题，因为不光在测试集上误差增大，训练集本身误差也会增大。如图示：

为什么网络层级越深，而模型效果却变差？

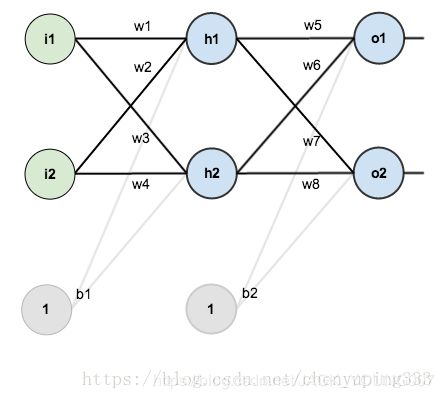
回顾一下最简单的神经网络结构，由输入层、隐藏层、输入层构成：

神经网络反向传播原理，先通过正向传播计算出 output，然后与真实样本比较并计算得出误差值 Etotal：

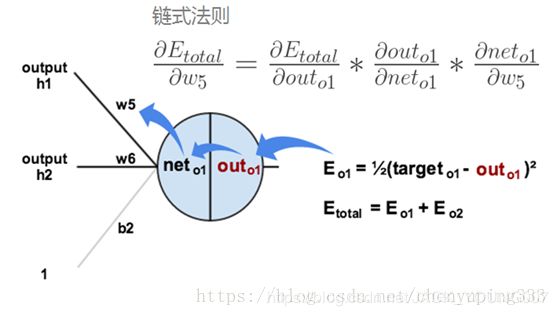
根据误差结果，利用 “链式求导法则” 求偏导，使结果误差反向传播从而得出各层的权重 w 调整的梯度。下图是输出结果到隐藏层的反向传播过程：（隐藏层到输入层的反向传播过程是类似）

通过不断的迭代，对参数矩阵进行不断调整后，使得输出结果的误差值更小，使得输出结果与事实更加接近。从上面的过程可以看出，神经网络在反向传播过程中要不断的传播梯度，当网络层数加深时，梯度在传播过程中会逐渐消失，导致无法对前面的网络层的权重进行有效的调整。

那么，如何在加深网络层数的同时，既能解决梯度消失问题，又能提升模型精度呢？ ResNet 应运而生。

深度残差网络（Deep Residual Network，简称DRN）

不断加深神经网络的层数，模型准确率会先上升然后达到饱和，再持续增加网络层数的时候则会导致准确率下降，示意图如下：

作出一个假设：假设现有一个比较浅的网络（Shallow Net）已达到了饱和的准确率，这时在它后面再加上几个恒等映射层（Identify mapping，即 y = x，输出等于输入），这样就增加了网络的深度，并且起码误差不会增加，即更深的网络不会带来训练集上的误差上升。这里提到的 “使用恒等映射直接将前一层输出传到后面” 的思想，便是深度残差网络的灵感来源。

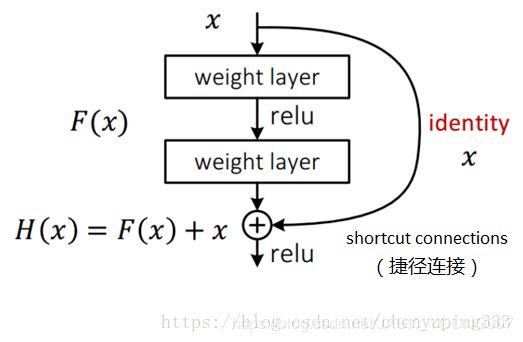
ResNet 引入残差网络结构 （residual network），通过这种残差网络结构，可以把网络层弄得很深（目前可达1000+层），并且最终的分类效果也非常好，残差网络的基本结构如图示：（该图带有跳跃结构）

残差网络借鉴了高速网络（Highway Network）的跨层链接思想，但对其进行了改进。Highway Network 残差项原本是带权值的，但 ResNet 采用恒等映射代替它。

假定某段神经网络的输入是x，期望输出是H(x)，即H(x) 是期望的复杂潜在映射。如果要学习这样的模型，则训练难度会比较大；回想前面的假设，如果已经学习到较饱和的准确率（或者当发现某一层的误差变大时），那么接下来的学习目标就转变为恒等映射的学习，也就是使输入 x 近似于输出 H(x)，以保持在后面的层次中不会造成精度下降。

在上面的残差网络结构图中，通过 “shortcut connections（捷径连接）” 的方式，直接把输入 x 传到输出作为初始结果，输出结果为 H(x) = F(x) + x，当 F(x) =0 时，那么 H(x) = x， 也就是上面提到的恒等映射。于是 ResNet 相当于将学习目标改变了，不再是学习一个完整的输出，而是目标值 H(x) 和 x 的差值，也就是所谓的残差 F(x) = H(x) - x，因此，后面的训练目标就是将残差结果逼近于0，使得随着网络层数加深，准确率不下降。

这种残差跳跃式的结构，打破了传统的神经网络 n-1 层的输出只能给 n 层作为输入的惯例，使某一层的输出可以直接跨过几层作为后面一层的输入，其意义在于为叠加多层网络而使得整个学习模型的错误率不降反升的难题提供了新的方向。至此神经网络的层数可以跨越之前的约束，达到几十层、上百层甚至千层，为高级语义特征提取和分类提供了可行性。

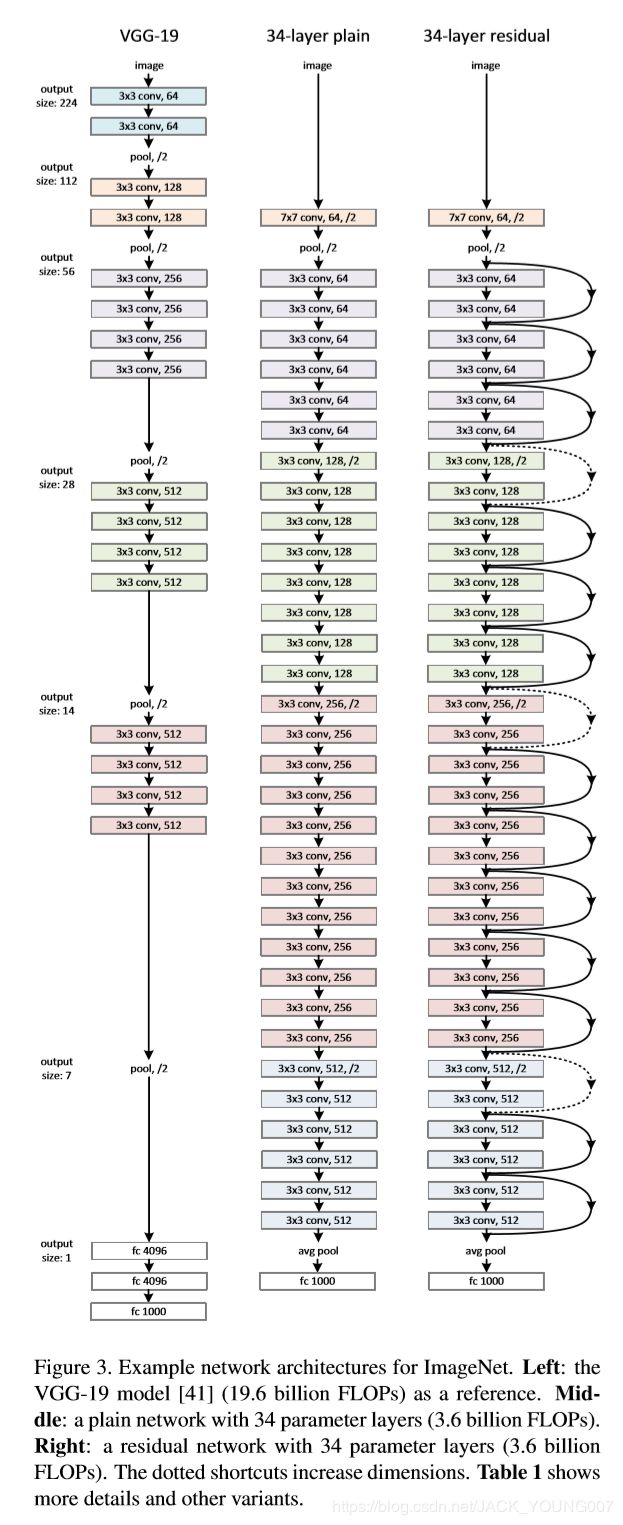
下图是论文中所提供：

 

从图中可以看出，“shortcut connections （捷径连接）”具有实线和虚线之分，其区别主要在于：

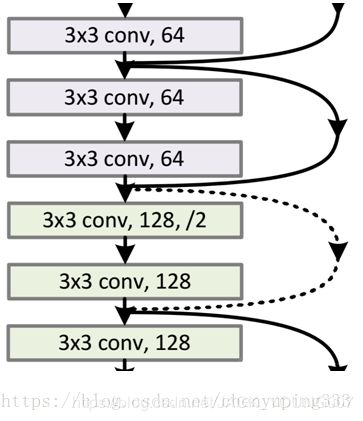
因为经过 “shortcut connections （捷径连接）”后， H(x) = F(x) + x， 如果 F(x) 和 x 的通道数相同，则可直接相加，如果通道数不同时，则不能直接相加。（前提条件是 feature map 的大小也是相同的）图中的实线和虚线就是为了区分这两种情况的：

--实线的 connection 部分，表示通道数相同，如上图的第一个粉色矩形和第三个粉色矩形，都是64通道的，feature map 也是相同的，所以采用计算方式为 H(x) = F(x) +x

--虚线的 connection 部分，表示通道数不同，如上图的第一个绿色矩形和第三个绿色矩形，分别是64通道和128通道，通道不同，采用的计算方式 H(x) = F(x) + Wx，其中 W 是卷积操作，用来调整维度的。

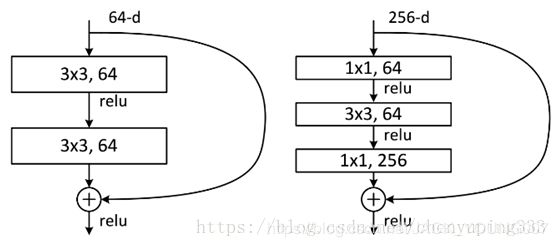
论文中除了提到两层残差学习单元，还提到三层的残差学习单元，如图示：

两种结构分别针对 ResNet34 （左图）和 ResNet50/101/152 （右图），其主要目的就是为了降低参数的数目。左图是两个 3*3 的卷积，参数数目为 3*3*256*256*2 = 1179648（上图是64通道，为保证计算具有对比性，调整为与右图一致的通道数256）.右图第一个卷积核把256维通道数降为64维，然后在最后面通过 1*1 卷积恢复，整体上用的参数数目： 1*1*256*64+ 3*3*64*64 + 1*1*64*256 = 69632，右图的参数数量比左图减少了约17倍。因此，右图主要目的就是为了减少参数量，从而减少计算量。

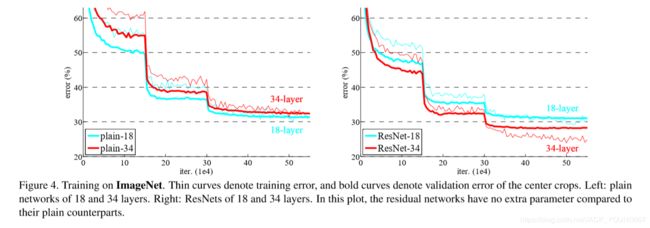
经检验测试，深度残差网络的确解决了退化问题，如下图示：左图平原网络（plain network）网络层次越深（34层）比网络层次浅的（18层）的误差率更高；右图残差网络 ResNet 的网络层次越深（34层）比网络层次浅的（18层）的误差率更低。