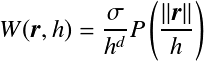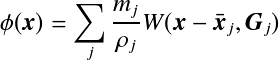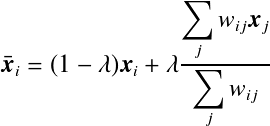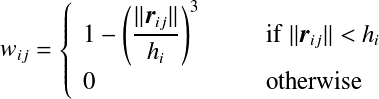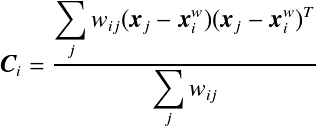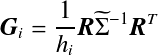【CG物理模拟系列】粒子法--表面生成手法(上)
使用粒子法模拟水流时,水流表面的生成主要分成如下两部分。
表面隐函数
- Muller的色彩函数 [1]
- Zhu and Bridson的方法 [2]
- Adams等的方法 [3]
- Anisotropic Kernel [4]
- Upsampling法 [5]
生成网格(Mesh)
- Marching Cubes(MC) [6]
- Regularised marching tetrahedra(RMT) [7]
- Screen Space Mesh [8], [9]
各向异性内核函数(Anisotropic kernel)
从粒子中生成隐函数的时候,使用下式这样的平滑化内核函数。
其中,![]() 是换算系数,
是换算系数,![]() 是模拟的次元数,
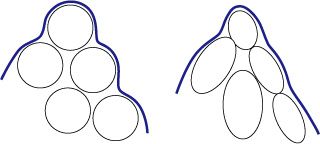
是模拟的次元数, ![]() 是local support(距离变远时值平滑减小)的对称函数。 这个定义类似于所谓的元球技术(Metaball), 生成的表面呈凹凸不平状(下图左)。像这样的表面我们称为blobby面。
是local support(距离变远时值平滑减小)的对称函数。 这个定义类似于所谓的元球技术(Metaball), 生成的表面呈凹凸不平状(下图左)。像这样的表面我们称为blobby面。
为了改进blobby的表面形状,Yu等人[10] 导入了各向异性内核(anisotropic kernel)来取代之前的各向同性内核。 也就是,使用正定矩阵![]() 来代替
来代替![]() ,
,
![]()
此时,矩阵![]() 中包含了旋转和伸缩变换,并且使用椭圆来取代球形状。通过把法线方向设定成椭圆短轴所在的方向,可以得到下图右侧这样平滑且边缘清晰的表面。另外,为了消除靠近表面粒子的不规则分布,也将粒子位置的关联函数进行平滑化处理,计算更新后位置
中包含了旋转和伸缩变换,并且使用椭圆来取代球形状。通过把法线方向设定成椭圆短轴所在的方向,可以得到下图右侧这样平滑且边缘清晰的表面。另外,为了消除靠近表面粒子的不规则分布,也将粒子位置的关联函数进行平滑化处理,计算更新后位置![]() 。对于全部的流体粒子,通过计算
。对于全部的流体粒子,通过计算![]() 和
和![]() 我们可以得到下式这样的隐函数场。
我们可以得到下式这样的隐函数场。
下面我们对参考文献[10]的![]() ,
,![]() 的计算方法进行详细说明。
的计算方法进行详细说明。
粒子位置的更新
为了修正不规则的粒子的位置,使用下面的Laplacian平滑处理来更新粒子的中心坐标。
![]() 是常数项,[10]中推荐使用0.9~1之间的值。这里的
是常数项,[10]中推荐使用0.9~1之间的值。这里的 ![]() 是加权函数,计算如下
是加权函数,计算如下
这里的加权函数通过计算协方差矩阵来计算各向异性。 为了能较为准确的计算各向异性,需要包含较多的流体粒子,因此上式中的有效半径![]() 设定为流体模拟用的有效半径的2倍大小。
设定为流体模拟用的有效半径的2倍大小。
另外,这里的![]() 仅用于表面的生成,而非流体模拟处理。 因此,更新前的位置
仅用于表面的生成,而非流体模拟处理。 因此,更新前的位置![]() 会储存在其他变量里。
会储存在其他变量里。
协方差矩阵的计算
为了得到![]() ,这里使用加权主成分分析法(WPCA:Weighted Principal Component Analysis)[11]进行计算。 主成分分析(PCA)是一种常用于图像识别领域的数据解析手法,可以根据分散数据的特征值生成新的坐标轴(主轴)以减少数据量。WPCA是在PCA中增加了各个数据的加权,可以更好的处理异常点(outlier)或噪音。
,这里使用加权主成分分析法(WPCA:Weighted Principal Component Analysis)[11]进行计算。 主成分分析(PCA)是一种常用于图像识别领域的数据解析手法,可以根据分散数据的特征值生成新的坐标轴(主轴)以减少数据量。WPCA是在PCA中增加了各个数据的加权,可以更好的处理异常点(outlier)或噪音。
在WPCA法中,我们首先计算各数据点的权重,然后根据权重求出其协方差矩阵(covariance matrix)![]() , 最后,对
, 最后,对![]() 进行特征值分析求得特征值,并把具有较大特征值所在的特征向量设定为新的主轴。最后,从WPCA所得结果中计算
进行特征值分析求得特征值,并把具有较大特征值所在的特征向量设定为新的主轴。最后,从WPCA所得结果中计算![]() 。
。
首先,计算加权后的平均位置![]() 。
。
![]() 指粒子
指粒子![]() 的临近粒子的中心。 通过使用权重
的临近粒子的中心。 通过使用权重![]() ,可以极大的减少距离
,可以极大的减少距离![]() 很远的异常点的影响。
很远的异常点的影响。
通过从![]() 到周围的各临近粒子的位置
到周围的各临近粒子的位置![]() 的向量的积,计算协方差矩阵。
的向量的积,计算协方差矩阵。
这里使用的加权函数![]() 与粒子位置更新时所使用的相同。
与粒子位置更新时所使用的相同。
协方差矩阵特征值分解
为了得到椭圆的伸缩方向,我们将协方差矩阵![]() 进行特征值分解,计算特征值和特征向量。
进行特征值分解,计算特征值和特征向量。
![]() 是各列特征向量的旋转矩阵,
是各列特征向量的旋转矩阵,![]() 是对角矩阵。为了应对大幅度变形或者临近粒子很少的孤立粒子等情况,我们进行如下处理来修正
是对角矩阵。为了应对大幅度变形或者临近粒子很少的孤立粒子等情况,我们进行如下处理来修正![]() 。
。
- 检查特征值防止大幅度变形发生。先把特征值从大到小排列, 当出现满足
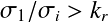 的
的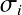 时,使用
时,使用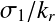 替换(
替换(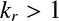 )。
)。 - 检查临近粒子数,找出孤立粒子。如果临近粒子数比
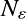 小时,让
小时,让 。这里的
。这里的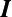 是单位矩阵,
是单位矩阵,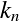 是控制内核大小的参数。
是控制内核大小的参数。 - 临近粒子全在的情况下,为了保持体积一定, 导入满足
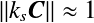 的
的 。 此时,修正后的协方差矩阵
。 此时,修正后的协方差矩阵 如下所示。
如下所示。

这里的![]() 。参考文献[11]中,使用的
。参考文献[11]中,使用的![]() 。
。
计算G
![]() 是
是![]() 的逆矩阵乘以
的逆矩阵乘以![]() 后的结果。
后的结果。
结果图
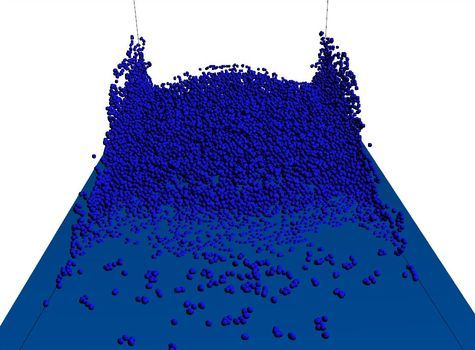
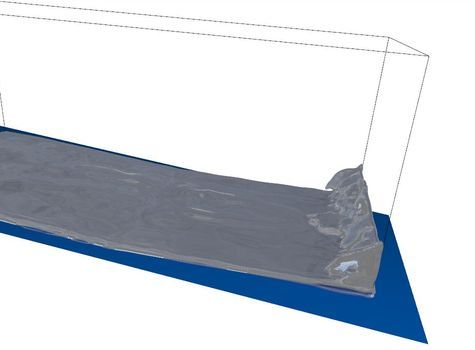
这里使用和【CG物理模拟系列】流体模拟--粒子法之SPH(实现)中类似场景,粒子数约25,000,网格化(MC法)的网格分辨率是256x103x103。
首先,应用协方差矩阵,把粒子当作椭圆体的绘图结果如下。
去掉网格面,使用GLSL绘制的折射面结果如下。
使用各向异性内核后的表面,不仅表面变得更加圆滑,也很好的再现了黏附在两侧墙壁上的薄层水膜。具体如下所示。
放大后如下。
去掉网格面,使用GLSL绘制的折射面结果如下。
大致计算时间,SPH计算:5ms/frame,各向异性内核中G的计算:10ms/frame,应用各向异性后网格化耗时:145ms/frame(以前的各向同性内核是15ms/frame)。这里的SPH的计算,各向异性内核的计算,和MC法网格化都是在GeForceGTX580显卡上,使用CUDA在GPU上测试得出的结果。
直接绘制粒子时,各向同性内核使用了Point Sprite,而各向异性内核则使用glutSolidSphere绘制椭圆。因此,绘制时间较久(我的环境下各向同性内核耗时85ms/frame,Point Sprite各向同性内核15ms/frame)。
参考文献
[1] M. Muller, D. Charypar and M. Gross, Particle-based Fluid Simulation for Interactive Applications, Proc. SCA2003, pp.154-159, 2003.
[2] Y. Zhu and R. Bridson, Animating sand as a fluid, Proc. SIGGRAPH 2005, pp.965-971, 2005.
[3] B. Adams, M. Pauly, R. Keiser and L. J. Guibas, Adaptively sampled particle fluids, Proc. SIGGRAPH2007, 48, 2007.
[4] J. Yu and G. Turk, Reconstructing Surfaces of Particle-Based Fluids Using Anisotropic Kernels, In Proceedings of the 2010 ACM SIGGRAPH/Eurographics symposium on Computer animation, 2010.
[5] B. Solenthaler, Y. Zhang and R. Pajarola, Efficient Refinement of Dynamic Point Data, Proc. Eurographics/IEEE VGTC Symposium on Point-Based Graphics, 2007.
[6] W. E. Lorensen and H. E. Cline, Marching cubes: a high resolution 3D surface construction algorithm, Computer Graphics (Proc. SIGGRAPH '87), 21, 163-169, 1987.
[7] G. M. Treece, R. W. Prager and A. H. Gee, Regularised marching tetrahedra: improved isosurface extraction, Computers and Graphics, 23, pp.583-598, 1999.
[8] M. Muller, S. Schirm and S. Duthaler, Screen space meshes, Proc. SCA2007, pp.9-15, 2007.
[9] W. J. van der Laan, S. Green and M. Sainz, Screen space fluid rendering with curvature flow, Proc. 2009 symposium on Interactive 3D graphics and games, pp.91-98, 2009.
[10] J. Yu and G. Turk, Reconstructing Surfaces of Particle-Based Fluids Using Anisotropic Kernels, In Proceedings of the 2010 ACM SIGGRAPH/Eurographics symposium on Computer animation, 2010.
[11] Y. Koren and L. Carmel, Visualization of labeled data using linear transformations, In Proceedings of IEEE Information Visualization, 2003.