第二章 第七节 线性回归（程序示例--多项式回归）

程序示例--多项式回归

下面，我们有一组温度（temperature）和实验产出量（yield）训练样本，该数据由博客 Polynomial Regression Examples 所提供：

temperature	yield
50	3.3
50	2.8
50	2.9
70	2.3
70	2.6
70	2.1
80	2.5
80	2.9
80	2.4
90	3.0
90	3.1
90	2.8
100	3.3
100	3.5
100	3.0

我们先通过如下预测函数进行训练：

# coding: utf-8
# linear_regression/test_temperature_normal.py
import regression
from matplotlib import cm
from mpl_toolkits.mplot3d import axes3d
import matplotlib.pyplot as plt
import matplotlib.ticker as mtick
import numpy as np

if __name__ == "__main__":
    X, y = regression.loadDataSet('data/temperature.txt');

    m,n = X.shape
    X = np.concatenate((np.ones((m,1)), X), axis=1)

    rate = 0.0001
    maxLoop = 1000
    epsilon =0.01

    result, timeConsumed = regression.bgd(rate, maxLoop, epsilon, X, y)

    theta, errors, thetas = result

    # 绘制拟合曲线
    fittingFig = plt.figure()
    title = 'bgd: rate=%.3f, maxLoop=%d, epsilon=%.3f \n time: %ds'%(rate,maxLoop,epsilon,timeConsumed)
    ax = fittingFig.add_subplot(111, title=title)
    trainingSet = ax.scatter(X[:, 1].flatten().A[0], y[:,0].flatten().A[0])

    xCopy = X.copy()
    xCopy.sort(0)
    yHat = xCopy*theta
    fittingLine, = ax.plot(xCopy[:,1], yHat, color='g')

    ax.set_xlabel('temperature')
    ax.set_ylabel('yield')

    plt.legend([trainingSet, fittingLine], ['Training Set', 'Linear Regression'])
    plt.show()

    # 绘制误差曲线
    errorsFig = plt.figure()
    ax = errorsFig.add_subplot(111)
    ax.yaxis.set_major_formatter(mtick.FormatStrFormatter('%.4f'))

    ax.plot(range(len(errors)), errors)
    ax.set_xlabel('Number of iterations')
    ax.set_ylabel('Cost J')

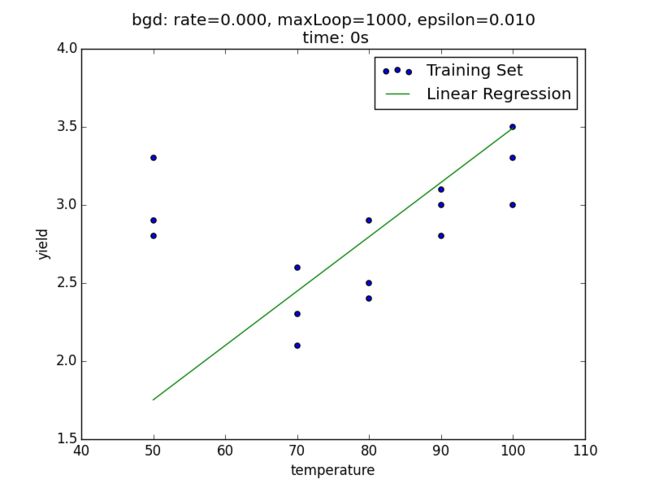
    plt.show()

得到的拟合图像为：

接下来，我们使用了多项式回归，添加了 2 阶项：

# coding: utf-8
# linear_regression/test_temperature_polynomial.py

import regression
import matplotlib.pyplot as plt
import matplotlib.ticker as mtick
import numpy as np

if __name__ == "__main__":
    srcX, y = regression.loadDataSet('data/temperature.txt');

    m,n = srcX.shape
    srcX = np.concatenate((srcX[:, 0], np.power(srcX[:, 0],2)), axis=1)
    # 特征缩放
    X = regression.standardize(srcX.copy())
    X = np.concatenate((np.ones((m,1)), X), axis=1)

    rate = 0.1
    maxLoop = 1000
    epsilon = 0.01

    result, timeConsumed = regression.bgd(rate, maxLoop, epsilon, X, y)
    theta, errors, thetas = result

    # 打印特征点
    fittingFig = plt.figure()
    title = 'polynomial with bgd: rate=%.2f, maxLoop=%d, epsilon=%.3f \n time: %ds'%(rate,maxLoop,epsilon,timeConsumed)
    ax = fittingFig.add_subplot(111, title=title)
    trainingSet = ax.scatter(srcX[:, 1].flatten().A[0], y[:,0].flatten().A[0])

    print theta

    # 打印拟合曲线
    xx = np.linspace(50,100,50)
    xx2 = np.power(xx,2)
    yHat = []
    for i in range(50):
        normalizedSize = (xx[i]-xx.mean())/xx.std(0)
        normalizedSize2 = (xx2[i]-xx2.mean())/xx2.std(0)
        x = np.matrix([[1,normalizedSize, normalizedSize2]])
        yHat.append(regression.h(theta, x.T))
    fittingLine, = ax.plot(xx, yHat, color='g')

    ax.set_xlabel('Yield')
    ax.set_ylabel('temperature')

    plt.legend([trainingSet, fittingLine], ['Training Set', 'Polynomial Regression'])
    plt.show()

    # 打印误差曲线
    errorsFig = plt.figure()
    ax = errorsFig.add_subplot(111)
    ax.yaxis.set_major_formatter(mtick.FormatStrFormatter('%.2e'))

    ax.plot(range(len(errors)), errors)
    ax.set_xlabel('Number of iterations')
    ax.set_ylabel('Cost J')

    plt.show()

得到的拟合曲线更加准确：