集成学习(Ensemble Learning)：Boosting、Bagging、Random Forest、Stacking

集成学习(Ensemble Learning)

  集成学习主要有两个分类，一个是个体学习器存在强依赖关系、必须串行生成的序列化方法，以Boosting为代表。另外一种是个体学习器不存在强依赖关系、可同时生成的并行化方法，以Bagging和随机森林（Random Forest）为代表。同时，集成学习还有一种分两个层次组合学习器的方法，即Stacking方法。

---

Boosting

  boosting模型用一句话解释就是，用模型学习先前的模型的残差，具体boosting的原理可以看我的blog:提升方法(boost)。其中boosting方法的一个大杀器XGboost的原理可以看我的blog:梯度提升决策树(GBDT)与极端梯度提升(xgboost)算法。

---

Bagging

  bagging模型相对简单，记总数据量为N，把总数据划分成m个子数据集，划分的方法利用bootstrap(bootstrap下一段讲)，利用这m份子数据集分别学习m个基学习器，最后综合这m个基学习器的结果，若是分类问题，利用majority voting (多数投票) 进行综合，若是回归问题，直接平均即可。所以，简单把多个回归模型的结果进行平均是不叫集成学习的，至少缺少bootstrap这个过程。
  bootstrap(自助法)十分简单，是一种有放回的随机采样，设总数据量为N，利用有放回的随机采样从总数据中生成m个子数据集，每一个子数据集的总量也是N，当然每一个子数据集中存在重复现象，同时每一个子数据集也不可能包含所有的数据，每生成一个子数据集，大概有36.8%的数据未包含进去，36.8%这一值可以这样计算得到，在总数据N中随机一次采样，一个数据未被抽中的概率是$1-\frac{1}{N}$，进行N次有放回的采样，该数据仍然未被抽中的概率是$(1-\frac{1}{N}{)}^N$，如果N趋近于无穷，这个概率变为$\frac{1}{e}$，即36.8%，这一批未被抽取到的数据也被称为oob(out of bag, 袋外)样本，可以作为这一子数据集的验证集。

Random Forest

  随机森林是特殊的bagging方法，随机森林限定基学习器必须是决策树，同时在利用bootstrap进行采样生成子数据集的同时，也会对特征进行采样，如果把总数据表示成$N\times M$的矩阵，$N$是总记录数，$M$是总特征数，则随机森林会对这个矩阵的行和列都进行采样，来训练基学习器。利用随机森林进行分类的示意图如下：

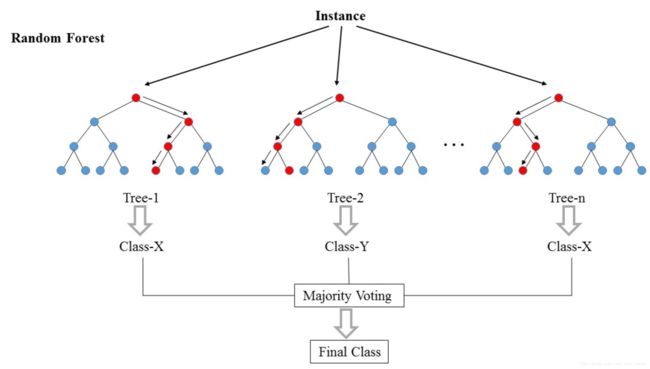
  随机森林可以输出特征重要度，这个特征重要度可以用于数据选择。

---

Stacking

  stacking方法的基本思路是，先用训练集$T=\{(x_1,y_1),(x_2,y_2),(x_3,y_3)\dots (x_n,y_n)\}$训练$m$个基学习器，这$m$个基学习器对$T$中的第$i$条记录分别有自己的输出结果，记为向量$$(x_{i1},x_{i2},x_{i3}\dots x_{ij}\dots x_{im}),i=1\dots n$$其中，$x_{ij}$表示第$j$个基学习器对训练集第$i$条记录的预测结果，对这一向量加上对应的实际输出$y_i$得到次级训练集如下$$\{\dots ((x_{i1},x_{i2},x_{i3}\dots x_{im}),y_i)\dots \},i=1\dots n$$用这个次级训练集训练一个额外的次级学习器，m个基学习器加上一个次级学习器就构成了stacking集成学习算法步骤。

  当需要使用stacking方法训练好的模型时，只需按上述步骤把数据分别代入$m$个基学习器，再把基学习器输出代入次级学习器，即可得到最终的输出。

  但这种方法存在一个致命的问题，我们用了m+1个学习器，翻来覆去都在学习一个训练集，最终得到的模型一定十分拟合训练集数据，极易造成过拟合问题。解决的方法是引入k折交叉验证方法。即把训练集T平均分成k份，下图以k=5为例。

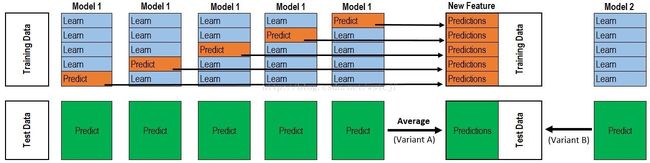
我们用k-1份训练数据训练基学习器，在把这个训练好的基学习器作用到剩下的1份训练集数据，这样我们就相当于得到了次级训练集的$\frac{1}{k}$，对剩余的k-1份也用上述方法，就得到了剩余的k-1个次级训练集的$\frac{1}{k}$，组合在一起就得到了完整的次级训练集，训练次级学习器即可。

算法的详细步骤如下：

算法流程

输入：训练集$Train=\{(x_1,y_1),(x_2,y_2),(x_3,y_3)\dots (x_n,y_n)\}$，交叉验证折叠参数k，m个基学习器方法，1个次级学习器方法；
输出：stacking模型；
执行流程：

1. 把训练集平均分成k份，记为$T_1,T_2\dots T_k$；
2. 对m个基学习器，均用k折交叉验证的方法学习基学习器模型的模型参数，同时得到k份次级训练集的$\frac{1}{k}$的数据；
3. 把这k份数据简单的集合在一起，得到完整的次级训练集，并用次级训练集数据训练次级学习器。
4. 输出stacking模型。

测试与模型使用

  对于stacking模型的测试和使用步骤是一样的(不一样才麻烦了)，还看上图，我们把测试数据(或模型实际使用时的数据)输入stacking模型，根据上面算法，我们对每个基学习器(一共m个)，实际均学习了k个模型(模型参数不同，超参数一样)，把测试数据(或模型实际使用时的数据)分别用在这k个模型上，得到的输出结果平均一下，就是单个基学习器的期望输出，把每个基学习器的期望输出聚合成次级测试集(或次级模型实际使用时的数据)，输入到次级学习器，就得到了最终的输出。

---

参考文献：
随机森林（Random Forest）算法原理：https://blog.csdn.net/edogawachia/article/details/79357844
01 集成学习 - 概述、Bagging - 随机森林、袋外错误率：https://yq.aliyun.com/articles/667533
02 集成学习 - 特征重要度、Extra Tree、TRTE、IForest、随机森林总结: https://www.jianshu.com/p/311024d128ad