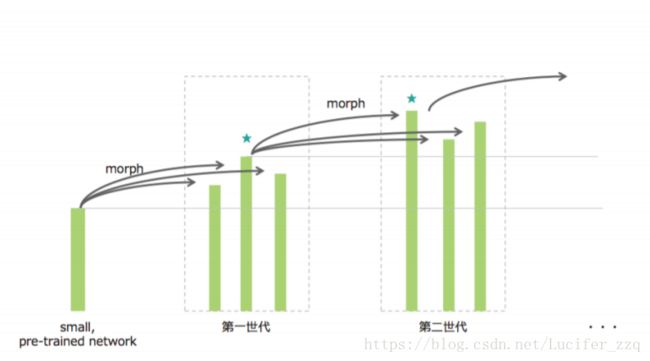
网络结构搜索(3) —— Simple and efficient architecture search for convolutional neural network
一、网络态射(Network Morphism)
神经网络的结构几乎都是朝着越来越深的方向发展,但是由人工来设计网络结构的代价非常大,在网络结构搜索(1)、网络结构搜索(2)中分析了NAS、ENAS的网络结构搜索方法,通过RNN来学习一个网络结构参数构建模型,ENAS又在NAS的基础上引入权值贡献(DAG图)提高了搜索效率。
本文则考虑到,在实际网络搜索中,对于某一个task会有一些前任已经训练好的模型,如何利用这些pre-train好的模型,不需要从头开始训练以及搜寻,提出了基于网络态射(network morphism)的搜索方法。
网络态射在论文中的定义:
简单的来说就是去对于原网络结构每一层寻找一个映射关系,可以做层之间的增加、改变通道数目、扩展宽度、跨层连接、加入ReLU激活层、merge等操作。
二、Hill Climbing以及一些数学基础:
求一个函数最大值的算法通常有:爬山算法、模拟退火算法、遗传算法。
(1)爬山算法是一种局部择优的方法,采用启发式方法,是对深度优先搜索的一种改进,它利用反馈信息帮助生成解的决策。
爬山算法一般存在以下问题:
- 局部最大
- 高地:也称为平顶,搜索一旦到达高地,就无法确定搜索最佳方向,会产生随机走动,使得搜索效率降低。
- 山脊:搜索可能会在山脊的两面来回震荡,前进步伐很小。
在本论文中理解则是:从搜索空间中产生临近的点,从中选择对应解最优的个体,替换原来的个体,并不断的重复。
最大的缺点在于非常容易陷入局部最优解,例如下图:
(2)模拟退火算法:
什么是“退火”:根据物理学原理,一个高温物体冷却的过程是:温度逐渐下降,并且下降的速率随时间推移而减小,最终与室温一致。
以上述爬山图为例,模拟退火的思路会放宽一些,即使是下一步的效果差一些,依旧给一定的转移概率,简单的来说就是:
- 若下一状态更优,则转移至下一状态
- 否则有一定的概率转移至下一状态
对于本论文来说,使用了余弦退火:将学习率设置为随模型迭代轮数不断改变的方法,更新学习率使用的是cos(),例如:
lr_scheduler = optim.lr_scheduler.CosineAnnealingLR(optimizer, T_max=5,eta_min=4e-08)
lr_scheduler.step()学习率变化则如下图:
同时文章使用了SGDR(热重启随机梯度下降,SGDR: Stochastic Grandient Descent with warm Restarted,ICLR 2017)作为优化器。每个epoch的学习率会被重新设置成原始超参数,然后在用余弦退火逐渐缩小,可以使得学习率变化为以下形态:
这样学习率的好处在于可以有更大的机会跳出局部最优解:
三、NAS by hill climbing:
算法过程如下:
主要思路:
(1)将某个pre-trained好的网络结构model0当做modelbest,这是网络的初始化
(2)开始做爬山算法:
当小于总共要走的nsteps时:
1、对上一代的modelbest做nneigh-1个映射:
![]()
并对这nneign-1个model采用SGDR的优化器,训练epochneigh次更新网络参数:
![]()
2、对原本的modelbest的model采用SGDR的优化器,训练epochneigh次更新网络参数:
![]()
最终得到更新后nneigh个model。
3、对这更新后的nneigh个model在验证集上进行测试,选择精度最高的作为此轮迭代后的modelbest:
对1-3次循环迭代。
四、ApplyNetMorphs:
Type I: Addition of layer (including regularization layer)
⽤Replace替换。当A=1,B=0时(可以学习初始值A=1,B=0,这与下⾯的Morph相同),这显然满⾜了这个假设。 它只是通过对当前图层进⾏加权来为其添加偏置,因此可以⽤来添加所谓的图层。还可以定义⼀个执⾏输出正则化的层(批处理标准化等)。很显然,当假设 C=A^-1,d=-cb 时,这个假设是成⽴ 的。
Type II: Output Concat
替换fiwi(x)=Ahwh(x)+b。这显然满⾜A〜= 0时的假设。这意味着在 h〜= h的情况下,⽹络的⼤⼩将会扩⼤,如果h(�)是⼀个连续的 隐层,h〜(x)是x,则可以表示连接类型Skip - Connection
TypeIII: Addition of ReLU
把这一层的权重简单的进行一个替换,例如拿来加relu。
Type IV: Output Merge
λ=1时保持不变,λ≠1时理论上可以合并 各种非线性函数。
Details:
Morph是随机选择的
for type I:添加layers的地⽅是随机的,kernel的size只有{3,5},通道数量与最新的卷积核数⽬相同
for type II:扩展宽度从2到4倍随机选择,要跳过的层的范围(i到j)是随机选择的(同样在tvpe IV中)
使⽤余弦退⽕来学习变形⽹络根据余弦曲线提⾼和降低学习率的⽅法将错误率降低约1%的效果。
五、Summary and Contributions:
通过逐渐发展⽹络,不需要从零开始学习。
可以评估降低结构搜索的速度和成本的观点。
然⽽,变形和启发式并没有太多的变化,⽽且它似乎可以轻松达到像Dense / ResNet这样的简单结构。
即使没有⼤规模的计算资源,也能⾃动设计⽹络架构 我们的算法很容易扩展 。