论文分享-->word2Vec论文总结
一直以来,对 word2vec ,以及对 tensorflow 里面的 wordEmbedding 底层实现原理一直模糊不清,由此决心阅读 word2Vec 的两篇原始论文, Efficient Estimation of Word Representations in Vector Space , Distributed Representations of Words and Phrases and their Compositionality ,看完以后还是有点半懂半不懂的感觉,于是又结合网上的一些比较好的讲解(Word2Vec Tutorial - The Skip-Gram Model),以及开源的实现代码理解了一遍,在此总结一下。
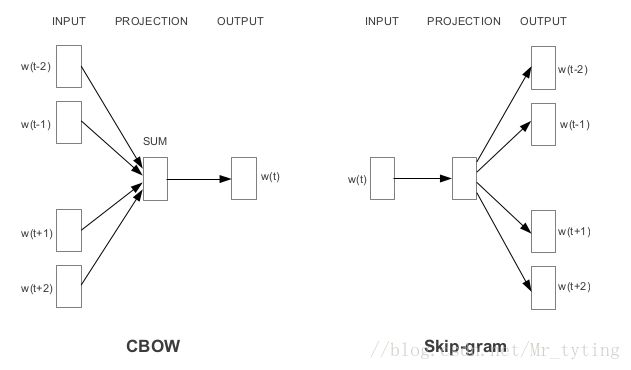
下面主要以 skip−gram 模型来介绍 word2Vec 。
word2vec工作流程
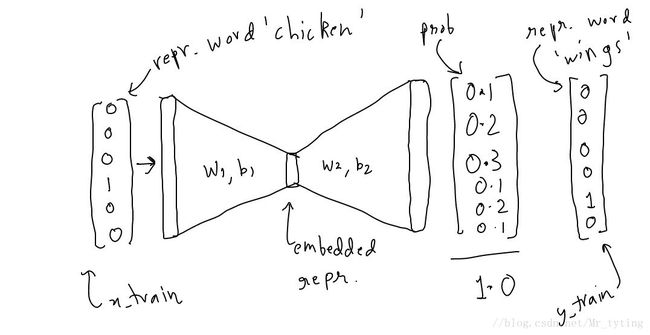
- word2Vec 只是一个三层 的神经网络。
- 喂给模型一个 word ,然后用来预测它周边的词。
- 然后去掉最后一层,只保存 input_layer 和 hidden_layer 。
- 从词表中选取一个词,喂给模型,在 hidden_layer 将会给出该词的 embedding repesentation 。
import numpy as np
import tensorflow as tf
corpus_raw = 'He is the king . The king is royal . She is the royal queen '
# convert to lower case
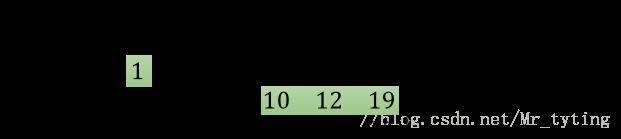
corpus_raw = corpus_raw.lower()上述代码非常简单和易懂,现在我们需要获取 input output pair ,假设我们现在有这样一个任务,喂给模型一个词,我们需要获取它周边的词,举例来说,就是获取该词前 n 个和后 n 个词,那么这个 n 就是代码中的 window_size ,例如下图:
注意:如果这个词是一个句子的开头或结尾, window 忽略窗外的词。
我们需要对文本数据进行一个简单的预处理,创建一个 word2int 的字典和 int2word 的字典。
words = []
for word in corpus_raw.split():
if word != '.': # because we don't want to treat . as a word
words.append(word)
words = set(words) # so that all duplicate words are removed
word2int = {}
int2word = {}
vocab_size = len(words) # gives the total number of unique words
for i,word in enumerate(words):
word2int[word] = i
int2word[i] = word来看看这个字典有啥效果:
print(word2int['queen'])
-> 42 (say)
print(int2word[42])
-> 'queen'好,现在可以获取训练数据啦
data = []
WINDOW_SIZE = 2
for sentence in sentences:
for word_index, word in enumerate(sentence):
for nb_word in sentence[max(word_index - WINDOW_SIZE, 0) : min(word_index + WINDOW_SIZE, len(sentence)) + 1] :
if nb_word != word:
data.append([word, nb_word])上述代码就是切句子,然后切词,得出的一个个训练样本 [word, nb_word] ,其中 word 就是模型输入, nb_word 就是该词周边的某个单词。
把 data 打印出来看看?
print(data)
[['he', 'is'],
['he', 'the'],
['is', 'he'],
['is', 'the'],
['is', 'king'],
['the', 'he'],
['the', 'is'],
['the', 'king'],
.
.
.
]现在我们有了训练数据了,但是需要将它转成模型可读可理解的形式,这时,上面的 word2int 字典的作用就来了。
来,我们更进一步的对 word 进行处理,并使其转成 one−hot 向量
i.e.,
say we have a vocabulary of 3 words : pen, pineapple, apple
where
word2int['pen'] -> 0 -> [1 0 0]
word2int['pineapple'] -> 1 -> [0 1 0]
word2int['apple'] -> 2 -> [0 0 1]那么为啥是 one−hot 特征呢?稍后将解释。
# function to convert numbers to one hot vectors
def to_one_hot(data_point_index, vocab_size):
temp = np.zeros(vocab_size)
temp[data_point_index] = 1
return temp
x_train = [] # input word
y_train = [] # output word
for data_word in data:
x_train.append(to_one_hot(word2int[ data_word[0] ], vocab_size))
y_train.append(to_one_hot(word2int[ data_word[1] ], vocab_size))
# convert them to numpy arrays
x_train = np.asarray(x_train)
y_train = np.asarray(y_train)利用 tensorflow 建立模型
# making placeholders for x_train and y_train
x = tf.placeholder(tf.float32, shape=(None, vocab_size))
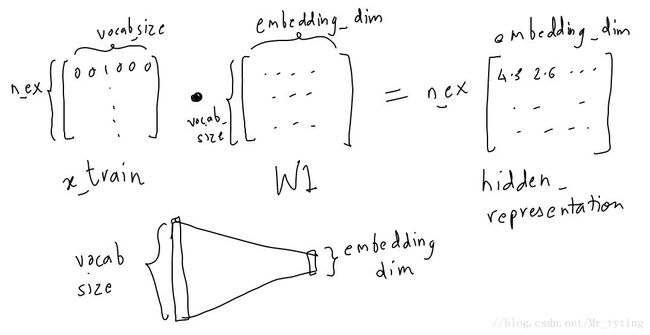
y_label = tf.placeholder(tf.float32, shape=(None, vocab_size))由上图,我们可以看出,我们将 input 转换成 embedding_representation ,并且将 vocabSize 维度降低到设定的 embedding_dim 。
EMBEDDING_DIM = 5 # you can choose your own number
W1 = tf.Variable(tf.random_normal([vocab_size, EMBEDDING_DIM]))
b1 = tf.Variable(tf.random_normal([EMBEDDING_DIM])) #bias
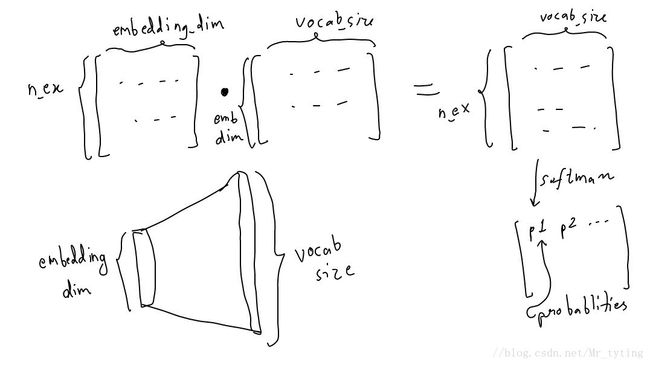
hidden_representation = tf.add(tf.matmul(x,W1), b1)接下来,我们需要使用 softmax 函数来预测该 word 周边的词。
W2 = tf.Variable(tf.random_normal([EMBEDDING_DIM, vocab_size]))
b2 = tf.Variable(tf.random_normal([vocab_size]))
prediction = tf.nn.softmax(tf.add( tf.matmul(hidden_representation, W2), b2))所以整体的过程如下:
input_one_hot ---> embedded repr. ---> predicted_neighbour_prob
predicted_prob will be compared against a one hot vector to correct it.好了,来看看怎么训这个模型
sess = tf.Session()
init = tf.global_variables_initializer()
sess.run(init) #make sure you do this!
# define the loss function:
cross_entropy_loss = tf.reduce_mean(-tf.reduce_sum(y_label * tf.log(prediction), reduction_indices=[1]))
# define the training step:
train_step = tf.train.GradientDescentOptimizer(0.1).minimize(cross_entropy_loss)
n_iters = 10000
# train for n_iter iterations
for _ in range(n_iters):
sess.run(train_step, feed_dict={x: x_train, y_label: y_train})
print('loss is : ', sess.run(cross_entropy_loss, feed_dict={x: x_train, y_label: y_train}))在训的过程中,你可以看到 loss 的变化:
loss is : 2.73213
loss is : 2.30519
loss is : 2.11106
loss is : 1.9916
loss is : 1.90923
loss is : 1.84837
loss is : 1.80133
loss is : 1.76381
loss is : 1.73312
loss is : 1.70745
loss is : 1.68556
loss is : 1.66654
loss is : 1.64975
loss is : 1.63472
loss is : 1.62112
loss is : 1.6087
loss is : 1.59725
loss is : 1.58664
loss is : 1.57676
loss is : 1.56751
loss is : 1.55882
loss is : 1.55064
loss is : 1.54291
loss is : 1.53559
loss is : 1.52865
loss is : 1.52206
loss is : 1.51578
loss is : 1.50979
loss is : 1.50408
loss is : 1.49861
.
.
.最终 loss 会收敛,即使其 accuracy 不能达到很高的水平,我们并不 care 这点,我们最终的目的是获取较好的 W1 和 b1 ,也就是 hidden_repesentation 。
为什么是 one−hot ?
当我们用 one−hot 向量乘以 W1 时,获取的是 W1 矩阵的某一行,所以 W1 扮演的是一个 look up table 。
在我们这个代码例子中,可以看看 "queen" 在 W1 中的 repesetation 。
print(vectors[ word2int['queen'] ])
# say here word2int['queen'] is 2
->
[-0.69424796 -1.67628145 3.07313657 -1.14802659 -1.2207377 ]给定一个向量,我们可以获取与其最近的向量
def euclidean_dist(vec1, vec2):
return np.sqrt(np.sum((vec1-vec2)**2))
def find_closest(word_index, vectors):
min_dist = 10000 # to act like positive infinity
min_index = -1
query_vector = vectors[word_index]
for index, vector in enumerate(vectors):
if euclidean_dist(vector, query_vector) < min_dist and not np.array_equal(vector, query_vector):
min_dist = euclidean_dist(vector, query_vector)
min_index = index
return min_index我们来看看,与 "king"、"queen"、"royal" 最近的词:
print(int2word[find_closest(word2int['king'], vectors)])
print(int2word[find_closest(word2int['queen'], vectors)])
print(int2word[find_closest(word2int['royal'], vectors)])
->
queen
king
he进阶
上面总结的主要是第一篇论文 Efficient Estimation of Word Representations in Vector Space 内的内容,虽然只是一个三层的神经网络,但是在海量训练数据的情况下,需要极大的计算资源来支撑整个过程,举例来说,我们设定的 embedding_size=300 时,而 vocab_size=10,000 时,这时 W1 矩阵的维度就达到了 10,000∗300=3million !!,这个时候再用 SGD 来优化训练过程就显得十分缓慢,但是有时候你必须使用大量的数据来训练模型来避免过拟合。论文 Distributed Representations of Words and Phrases and their Compositionality 介绍了几种解决办法。
- 采用下采样来降低训练样本数量
在 tensorflow 里面实现的 word2Vec , vocab_szie 并不是所有的 word 的数量,而且先统计了所有 word 的出现频次,然后选取出现频次最高的前 50000 的词作为词袋。具体操作请看代码 tensorflow/examples/tutorials/word2vec/word2vec_basic.py,其余的词用 unk 代替。 - 采用一种所谓的”负采样”的操作,这种操作每次可以让一个样本只更新权重矩阵中一小部分,减小训练过程中的计算压力。
举例来说:一个 input output pair 如: (“fox”,“quick”) ,由上面的分析可知,其 true label 为一个 one−hot 向量,并且该向量只是在 quick 的位置为1,其余的位置均为0,并且该向量的长度为 vocab size ,由此每个样本都缓慢能更新权重矩阵,而”负采样”操作只是随机选择其余的部分 word ,使得其在 true label 的位置为0,那么我们只更新对应位置的权重。例如我们如果选择负采样数量为5,则选取5个其余的 word ,使其对应的 output 为0,这个时候 output 只是6个神经元,本来我们一次需要更新 300∗10,000 参数,进行负采样操作以后只需要更新 300∗6=1800 个参数。
个人感觉 word2Vec 了解到这个程度差不多了。
完整代码:
import tensorflow as tf
import numpy as np
corpus_raw = 'He is the king . The king is royal . She is the royal queen '
# convert to lower case
corpus_raw = corpus_raw.lower()
words = []
for word in corpus_raw.split():
if word != '.': # because we don't want to treat . as a word
words.append(word)
words = set(words) # so that all duplicate words are removed
word2int = {}
int2word = {}
vocab_size = len(words) # gives the total number of unique words
for i,word in enumerate(words):
word2int[word] = i
int2word[i] = word
# raw sentences is a list of sentences.
raw_sentences = corpus_raw.split('.')
sentences = []
for sentence in raw_sentences:
sentences.append(sentence.split())
WINDOW_SIZE = 2
data = []
for sentence in sentences:
for word_index, word in enumerate(sentence):
for nb_word in sentence[max(word_index - WINDOW_SIZE, 0) : min(word_index + WINDOW_SIZE, len(sentence)) + 1] :
if nb_word != word:
data.append([word, nb_word])
# function to convert numbers to one hot vectors
def to_one_hot(data_point_index, vocab_size):
temp = np.zeros(vocab_size)
temp[data_point_index] = 1
return temp
x_train = [] # input word
y_train = [] # output word
for data_word in data:
x_train.append(to_one_hot(word2int[ data_word[0] ], vocab_size))
y_train.append(to_one_hot(word2int[ data_word[1] ], vocab_size))
# convert them to numpy arrays
x_train = np.asarray(x_train)
y_train = np.asarray(y_train)
# making placeholders for x_train and y_train
x = tf.placeholder(tf.float32, shape=(None, vocab_size))
y_label = tf.placeholder(tf.float32, shape=(None, vocab_size))
EMBEDDING_DIM = 5 # you can choose your own number
W1 = tf.Variable(tf.random_normal([vocab_size, EMBEDDING_DIM]))
b1 = tf.Variable(tf.random_normal([EMBEDDING_DIM])) #bias
hidden_representation = tf.add(tf.matmul(x,W1), b1)
W2 = tf.Variable(tf.random_normal([EMBEDDING_DIM, vocab_size]))
b2 = tf.Variable(tf.random_normal([vocab_size]))
prediction = tf.nn.softmax(tf.add( tf.matmul(hidden_representation, W2), b2))
sess = tf.Session()
init = tf.global_variables_initializer()
sess.run(init) #make sure you do this!
# define the loss function:
cross_entropy_loss = tf.reduce_mean(-tf.reduce_sum(y_label * tf.log(prediction), reduction_indices=[1]))
# define the training step:
train_step = tf.train.GradientDescentOptimizer(0.1).minimize(cross_entropy_loss)
n_iters = 10000
# train for n_iter iterations
for _ in range(n_iters):
sess.run(train_step, feed_dict={x: x_train, y_label: y_train})
print('loss is : ', sess.run(cross_entropy_loss, feed_dict={x: x_train, y_label: y_train}))
vectors = sess.run(W1 + b1)
def euclidean_dist(vec1, vec2):
return np.sqrt(np.sum((vec1-vec2)**2))
def find_closest(word_index, vectors):
min_dist = 10000 # to act like positive infinity
min_index = -1
query_vector = vectors[word_index]
for index, vector in enumerate(vectors):
if euclidean_dist(vector, query_vector) < min_dist and not np.array_equal(vector, query_vector):
min_dist = euclidean_dist(vector, query_vector)
min_index = index
return min_index
from sklearn.manifold import TSNE
model = TSNE(n_components=2, random_state=0)
np.set_printoptions(suppress=True)
vectors = model.fit_transform(vectors)
from sklearn import preprocessing
normalizer = preprocessing.Normalizer()
vectors = normalizer.fit_transform(vectors, 'l2')
print(vectors)
import matplotlib.pyplot as plt
fig, ax = plt.subplots()
print(words)
for word in words:
print(word, vectors[word2int[word]][1])
ax.annotate(word, (vectors[word2int[word]][0],vectors[word2int[word]][1] ))
plt.show()