卡尔曼滤波之目标跟踪
本文目录:
1.关于卡尔曼滤波理论学习
2.卡尔曼滤波的两个简单使用示例
3. 卡尔曼滤波二维平面目标跟踪中的应用
1.关于卡尔曼滤波理论学习
之前的博文有关于 卡尔曼滤波的资料,通俗易懂。这里总结一下Kalman的公式精华,输入麻烦,直接上自己之前的笔记了,如下:

最最重要的一点,在使用卡尔曼滤波之前,首先你得弄清楚你假设的动态系统模型(说白了还是调参,跟pid一样),然后直接使用算法就行了。
2.卡尔曼滤波的两个简单python使用示例
jupyter notebook写的。
import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline例子一:单一的真实值在高斯噪声影响下的卡尔曼滤波
原地址:python起步之卡尔曼滤波
#这里是假设A=1,H=1的情况
# intial parameters
n_iter = 50
sz = (n_iter,) # size of array
x = -0.37727 # truth value (typo in example at top of p. 13 calls this z)
z = np.random.normal(x,0.1,size=sz) # observations (normal about x, sigma=0.1)
Q = 1e-5 # process variance # allocate space for arrays
xhat=np.zeros(sz) # a posteri estimate of x
P=np.zeros(sz) # a posteri error estimate
xhatminus=np.zeros(sz) # a priori estimate of x
Pminus=np.zeros(sz) # a priori error estimate
K=np.zeros(sz) # gain or blending factor
R = 0.1**2 # estimate of measurement variance, change to see effect # intial guesses
xhat[0] = 0.0
P[0] = 1.0
for k in range(1,n_iter):
# time update
xhatminus[k] = xhat[k-1] #X(k|k-1) = AX(k-1|k-1) + BU(k) + W(k),A=1,BU(k) = 0
Pminus[k] = P[k-1]+Q #P(k|k-1) = AP(k-1|k-1)A' + Q(k) ,A=1
# measurement update
K[k] = Pminus[k]/( Pminus[k]+R ) #Kg(k)=P(k|k-1)H'/[HP(k|k-1)H' + R],H=1
xhat[k] = xhatminus[k]+K[k]*(z[k]-xhatminus[k]) #X(k|k) = X(k|k-1) + Kg(k)[Z(k) - HX(k|k-1)], H=1
P[k] = (1-K[k])*Pminus[k] #P(k|k) = (1 - Kg(k)H)P(k|k-1), H=1
plt.figure()
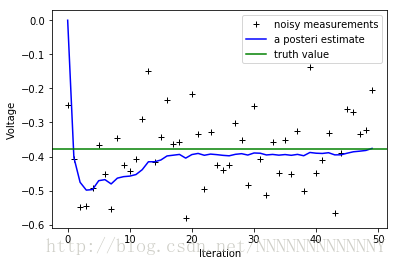
plt.plot(z,'k+',label='noisy measurements') #测量值
plt.plot(xhat,'b-',label='a posteri estimate') #过滤后的值
plt.axhline(x,color='g',label='truth value') #系统值
plt.legend()
plt.xlabel('Iteration')
plt.ylabel('Voltage')
plt.figure()
valid_iter = range(1,n_iter) # Pminus not valid at step 0
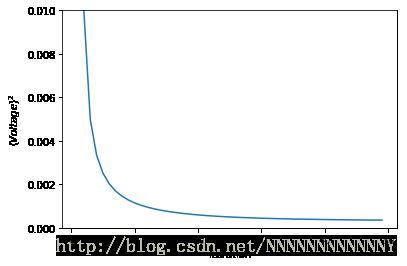
plt.plot(valid_iter,Pminus[valid_iter],label='a priori error estimate')
plt.xlabel('Iteration')
plt.ylabel('$(Voltage)^2$')
plt.setp(plt.gca(),'ylim',[0,.01])
plt.show() 例子二:估计体重
原地址:【卡尔曼滤波器-Python】The g-h filter , 有修改。
先大概看一下数据
z=np.array([158.0, 164.2, 160.3, 159.9, 162.1, 164.6, 169.6, 167.4, 166.4, 171.0, 171.2, 172.6])
x=np.arange(160, 172, 1)
er=z-x
plt.figure()
plt.scatter(er,np.zeros(12))
plt.show()
print('mean:',np.mean(er))
print('var:',np.var(er))mean: 0.108333333333
var: 4.50409722222
建立卡尔曼滤波的模型
xk=xk−1+1
zk=xk+vk
总结: A=1,B=1,uk=1,wk∼N(0,0)(即Qk=0),H=1,vk∼N(0,4.5)(即Rk=4.5)
# intial parameters
z=np.array([158.0, 164.2, 160.3, 159.9, 162.1, 164.6, 169.6, 167.4, 166.4, 171.0, 171.2, 172.6])
A=1
B=1
u_k=1
Q=0
H=1
R=4.5
# allocate space for arrays
sz=12
xhat=np.zeros(sz) # a posteri estimate of x
P=np.zeros(sz) # a posteri error estimate
xhatminus=np.zeros(sz) # a priori estimate of x
Pminus=np.zeros(sz) # a priori error estimate
K=np.zeros(sz) # gain or blending factor # intial guesses
xhat[0] = 160 #设为真实值
P[0] = 1.0
for k in range(1,sz):
# time update
xhatminus[k] = A*xhat[k-1]+B*u_k #X(k|k-1) = AX(k-1|k-1) + BU(k) + W(k),A=1,BU(k) = 0
Pminus[k] = A*P[k-1]*A+Q #P(k|k-1) = AP(k-1|k-1)A' + Q(k) ,A=1
# measurement update
K[k] = Pminus[k]*H/(H*Pminus[k]*H + R ) #Kg(k)=P(k|k-1)H'/[HP(k|k-1)H' + R],H=1
xhat[k] = xhatminus[k]+K[k]*(z[k]-xhatminus[k]) #X(k|k) = X(k|k-1) + Kg(k)[Z(k) - HX(k|k-1)], H=1
P[k] = (1-K[k])*Pminus[k] #P(k|k) = (1 - Kg(k)H)P(k|k-1), H=1 plt.figure()
plt.plot(z,'k+',label='noisy measurements') #测量值
plt.plot(xhat,'b-',label='a posteri estimate') #过滤后的值
plt.plot(x,color='g',label='truth value') #系统值
plt.legend()
plt.xlabel('Iteration')
plt.ylabel('weight')
3. 卡尔曼滤波二维平面目标跟踪中的应用用
opencv官方给了个一维的示例,在opencv\sources\samples\cpp下,首先要把这个搞懂吧。
参见:opencv官方文档 cv::KalmanFilter::KalmanFilter ( )
好,现在卡尔曼滤波肯定已经搞明白了。但是图像处理中的目标跟踪,我的观测值从哪来? 这句话简直太重要了,关于这个这的就因人而异了,卡尔曼滤波嘛,只是滤波而异,说白了是在最后一步对噪声的一个处理。至少我是这么想的,重点在于调参。
刚好最近做个东西用上二维下的目标跟踪,这里给个参考示例。
//加载数据,
import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline
import re
tip_coordinate_re=re.compile(r'^(\d+):\s(\d+)\s(\d+)$')
tip_coordinate_x=[]
tip_coordinate_y=[]
with open('endPoint_estimation.txt') as f:
for line in f.readlines():
tip_coordinate_x.append(float(tip_coordinate_re.match(line.strip()).group(2)))
tip_coordinate_y.append(float(tip_coordinate_re.match(line.strip()).group(3)))
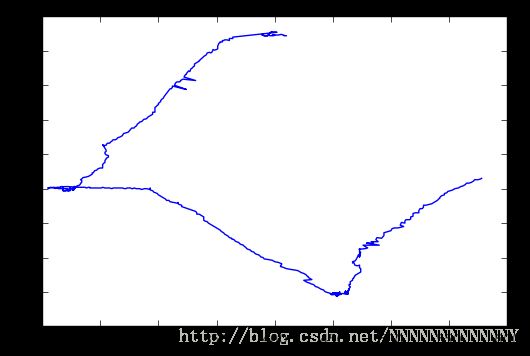
plt.plot(tip_coordinate_x, tip_coordinate_y, '-')
plt.show()(具体数据我这里就不给了,你可以用自己的或模拟一个)
//卡尔曼滤波
import numpy as np
import matplotlib.pyplot as plt
def kalman_xy(x, P, measurement, R,
motion = np.matrix('0. 0. 0. 0.').T,
Q = np.matrix(np.eye(4))):
"""
Parameters:
x: initial state 4-tuple of location and velocity: (x0, x1, x0_dot, x1_dot)
P: initial uncertainty convariance matrix
measurement: observed position
R: measurement noise
motion: external motion added to state vector x
Q: motion noise (same shape as P)
"""
return kalman(x, P, measurement, R, motion, Q,
F = np.matrix('''
1. 0. 1. 0.;
0. 1. 0. 1.;
0. 0. 1. 0.;
0. 0. 0. 1.
'''),
H = np.matrix('''
1. 0. 0. 0.;
0. 1. 0. 0.'''))
def kalman(x, P, measurement, R, motion, Q, F, H):
'''
Parameters:
x: initial state
P: initial uncertainty convariance matrix
measurement: observed position (same shape as H*x)
R: measurement noise (same shape as H)
motion: external motion added to state vector x
Q: motion noise (same shape as P)
F: next state function: x_prime = F*x
H: measurement function: position = H*x
Return: the updated and predicted new values for (x, P)
See also http://en.wikipedia.org/wiki/Kalman_filter
This version of kalman can be applied to many different situations by
appropriately defining F and H
'''
# UPDATE x, P based on measurement m
# distance between measured and current position-belief
y = np.matrix(measurement).T - H * x
S = H * P * H.T + R # residual convariance
K = P * H.T * S.I # Kalman gain
x = x + K*y
I = np.matrix(np.eye(F.shape[0])) # identity matrix
P = (I - K*H)*P
# PREDICT x, P based on motion
x = F*x + motion
P = F*P*F.T + Q
return x, P
def demo_kalman_xy():
x = np.matrix('0. 0. 0. 0.').T #initial state 4-tuple of location and velocity
P = np.matrix(np.eye(4))*1000 # initial uncertainty
# N = 20
# true_x = np.linspace(0.0, 10.0, N)
# true_y = true_x**2
# observed_x = true_x + 0.05*np.random.random(N)*true_x
# observed_y = true_y + 0.05*np.random.random(N)*true_y
observed_x = tip_coordinate_x
observed_y = tip_coordinate_y
plt.plot(observed_x, observed_y, 'ro')
result = []
# R = 0.01**2
R = 0.01**2
for meas in zip(observed_x, observed_y):
x, P = kalman_xy(x, P, meas, R)
result.append((x[:2]).tolist())
kalman_x, kalman_y = zip(*result)
plt.plot(kalman_x, kalman_y, 'g-')
plt.show()
demo_kalman_xy()
可以看到效果一般啦,具体还需要再调。
卡尔曼滤波部分的代码写得真好,声明不是本人所写,出自kalman 2d filter in python
。另外也可以参考下论文基于Kalman 预测的人体运动目标跟踪 。