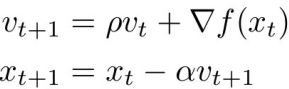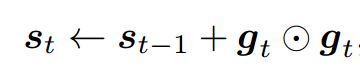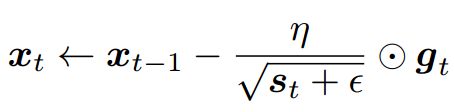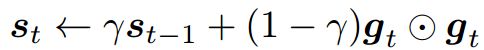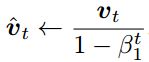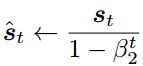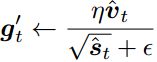深度学习中常见的参数优化方法

- SGD

                                                                          

与全量梯度下降相比,SGD的特点如下:

优点 : 由于每次只涉及一个样本,因此梯度计算速度很快;

缺点 : 每次计算梯度时只受单个样本的影响,所以导致梯度的准确度下降,可能会导致loss曲线的震荡

改进方案 : 可以采用MinBatch-GD,或者SGD + Momentum

- SGD + Momentum

                                                                  

通常将V0初始化为0, pho置为0.9或者0.99, 与SGD相比,在梯度更新时保留了上一步的梯度信息,从而使得梯度更加稳健.换个说法就是，如果当前计算出来的梯度方向与历史梯度方向不一致，则当前梯度会被历史梯度所修正（亦即：梯度衰减）。

                                                                         

            图1. SGD(black) vs SGD+Momentum(blue)          图2. SGD(black) vs SGD+Momentum(blue)  vs Nestrov (green)

- Nesterov Momentum

          　　　　　　　　　　　　　　        

Nesterov Momentum核心思想是：在计算当前梯度时，“向前”展望一下，这样往往会加速算法的收敛。其示意图如下所示：

                                    

SGD-Momentum是基于当前位置xt来计算梯度的；而Nesterov Momentum则是在展望点xt+rho*vt进行计算的。

一般而言，将上式变形 :　   ，我们可以得到与SGD-Momentum梯度更新的方式一致的表达形式：

　　　　　　　　　　　　　　　　  　 

- AdaGrad

以SGD的更新方式为例，对于每一个参数的训练都采用了相同的学习率alpha，相应的更新量为：，这种更新策略存在一个潜在的问题：对于那些取值比较大的分量，可能会导致“步子迈得太大”；对于那些取值比较小的分量，可能又存在“步子迈得太小”。而不论是前者还是后者，都可能会延缓了模型的收敛速度，为了缓解这种情况，AdaGrad算法做了如下修正：

                                                                            

                                                                                                    

其中，表示对应位置相乘，其核心思想是：通过将前t轮的梯度信息按照对应位置元素的平方和的形式进行累加，epsilon为平滑项，其取值一般为1e-8 ~ 1e-7，用来预防数值下溢。在AdaGrad算法中，不同的元素分别拥有⾃⼰的学习率，从而实现“因地制宜”，而不是SGD中的的“统一步调”。AdaGrad更新算法的缺点是：在训练的中后期，由于分母上梯度平方的累计效应，将会使得梯度趋于0，从而导致训练提前结束。

- RMSProp

RMSProp更新算法是由Geoff Hinton团队于2012年提出[1]，针对AdaGrad可能导致训练提前终止的缺点，它做了如下的改进：

                                                                        

                                                                         

其中，。RMSProp算法的核心思想是：通过将第t-1轮的状态变量和第t轮的梯度信息按照对应位置元素的平方和相加来生成第t轮的状态变量。与AdaGrad相比，在RMSProp中⾃变量每个元素的学习率在迭代过程中就不再⼀直降低，或者降低得速度相对缓慢一些。

- Adam

Adam是Adaptive moments的缩写，它由Diederik P. Kingma和Jimmy Ba于2014年提出[2]，是目前深度学习领域中应用非常广泛的优化方法。Adam算法结合了Momentum系列方法和RMSProp指数加权的移动平均策略，Momentum的更新格式如下：

                                                                              

其中， 0 ≤ β1 < 1（作者建议值为0.9），v0一般初始化为0. 中间状态变量更新如下：

                                                                        

其中，0 ≤ β2 < 1（作者建议取值为0.999），一般初始化为0.考虑到算法迭代初期，t取值较小，梯度信息的富集速度较慢，eg：当t=1时， v1 = 0.1g1，为了消除这样的影响，作者对更新后的v和s进行修正，具体格式如下：

                                                                   ，

利用修正后的v和s得到最终用于更新参数的修正梯度：

                                                                               

相应的参数迭代更新格式为：

                                                                         

参考文献：

[1]. Tieleman, T., & Hinton, G. (2012). Lecture 6.5-rmsprop: Divide the gradient by a running average of its recent magnitude. COURSERA: Neural networks for machine learning, 4(2), 26- 31.

[2]. Diederik P. Kingma, Jimmy Ba. Adam: A Method for Stochastic Optimization [arXiv-2014]