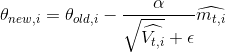深度学习中的参数优化方法
一、梯度下降法
: 学习率
1、批量梯度下降法
每次更新需要在整个数据集上求出
优点：如果loss是个凸函数，则批量梯度下降会在全局最小值处收敛；若loss非凸，则会收敛于局部最小值
缺点：1）更新速度慢
2）不能在线训练模型
3）如果数据集很大，内存无法容纳，则无法使用此方法训练模型
4）若loss非凸，陷入局部极小值后，很难跳入另一个更小的局部极小值
2、随机梯度下降法
每次更新只对数据集中的一个样本求
优点：1）更新速度快
2）能够在线学习
3）由于其在收敛过程中波动很大，容易帮助目标函数从一个局部极小值跳入另一个更小的局部极小值
缺点：由于其在收敛过程中波动较大，会使得其在收敛到特定最小值的过程很复杂，可能会持续波动而不停止
如果慢慢降低学习率，随机梯度下降表现出了与批量梯度下降法相似的收敛过程即：如果loss是个凸函数，则在全局最小值处收敛；若loss非凸，则会收敛于局部最小值
3、小批量梯度下降法
每次更新对m个样本构成的一个batch求
小批量梯度下降法集合了上述两种梯度下降法的优势
优点：1）相比于随机梯度下降法，降低了更新参数的方差，使收敛过程更加稳定
2）能够利用最新的深度学习程序库中高度优化的矩阵运算器，有效地求出每个 Batch数据的梯度
一般用SGD指代小批量梯度下降法
总结：梯度下降法面临的挑战：
1）选择合适的学习率，学习率太小，收敛速度太慢，学习率太大会阻碍收敛甚至在最小值处产生振荡，最终甚至可能导致结果发散
2）可以设置一个学习率列表，使得学习率按预先设置的学习率表变化（比如给loss设置的阈值来设定学习率的变化）
3）所有参数都采用相同的学习率；如果数据是稀疏的，某些特征出现的概率很小，我们希望较少出现的特征的系数具有更大的学习率
4）如何使目标函数跳出鞍点
tensorflow函数：
tf.train.GradientDescentOptimizer(alpha)二、动量法 Momentum
: 前 t 步积累的动量和
: 学习率
:衰减系数 <1
合并历史梯度和当前梯度作为动量，其中历史梯度前有一个小于1衰减系数，使得历史梯度的影响越来越小；动量项在梯度指向相同的方向逐渐增大，在梯度指向不同的方向逐渐减小
优点：1）加速收敛
2）减小振荡
tensorflow函数：
tf.train.MomentumOptimizer(alpha, gamma)三、Nesterov加速梯度法（NAG）
:表示将参数
按前t-1步积累的动量方向更新，计算得到的loss
：超前梯度
合并历史梯度和超前梯度
优点：相比于Momentum方法，NAG收敛速度明显加快，波动减小更多
tensorflow函数：
tf.train.MomentumOptimizer(alpha, gamma, use_nesterov=True)
四、Adagrad
将每个参数每次迭代的梯度取平方累加再开方，用基础学习率除以这个数来完成每个参数学习率的动态更新
梯度较大的参数应使用较小的学习率
: 初始学习率
随着t的增加，
会越来越大，学习率会越来越小；一般来说Adagrade算法一开始是激励收敛，到了后面就慢慢变成惩罚收敛，速度越来越慢。
优点：1）对不同的参数分别调整学习率，适合处理稀疏数据
2）不需要手工调节学习率
缺点：当迭代次数足够大之后，学习率不断减小最终变成无限小值，此时，这个算法已经不能从数据中学到额外的信息。
tensorflow函数：
tf.train.AdagradOptimizer(alpha, epsilon)五、Adadelta、RMSprop
Adadelta是Adagrad的一个延伸，为了解决Adagrad学习率单调下降的问题
Adadelta只计算固定时间窗口为w内梯度值的累积和，且梯度累积和为过去（w）梯度的衰减平均
六、Adam
同样为了解决Adagrad学习率单调下降的问题
Adam与Adadelta和RMSprop计算历史梯度衰减方式不同，它不使用历史平方衰减，其衰减方式类似动量
一般
Adam与其他几个自适应学习速率比较，效果均要好
tensorflow函数：
tf.train.AdamOptimizer(alpha, beta1, beta2, epsilon)六、总结
1、动量法和NAG都是为了解决梯度下降法的振荡问题，使其能快速收敛到极小值 （改变梯度的大小及方向）
2、Adagrad、Adadelta、RMSprop、Adam都是为了解决梯度下降法不同参数不同迭代次数学习率相同的问题 （改变学习率）
同时也能快速跳出鞍点