KMP算法

KMP算法

假如现在有一串字符串S:abcdefgabc,有一串模式串P:abcdd,要在字符串
S中查找P第一次出现的位置.

KMP算法原理

在描述KMP之前,先说一下暴力匹配算法:

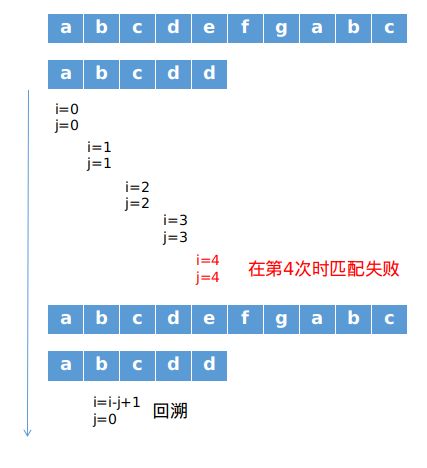
假设当前S字符串匹配到第i个位置,P字符串匹配到第j个位置,则:

• 若S[i]==P[j],说明匹配成功当前字符,则i++;j++,对下一个字符进行匹配
• 若S[i]!=P[i],说明当前字符匹配失败,则令i=i-j+1;j=0对字符串进行回溯

可以看出,在极端情况下,i可能回溯P.length-S.length次,而对于每次回溯都要重新遍历j的值,时间复杂度可达O(mn).

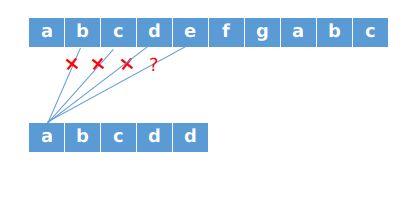
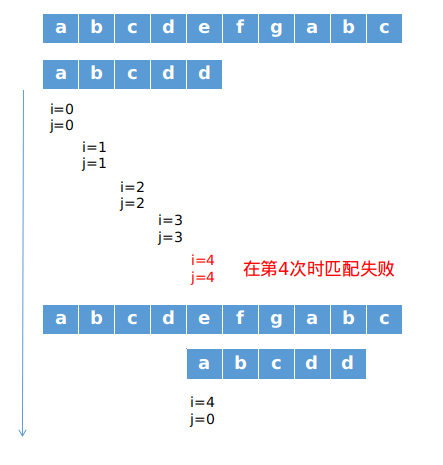
现在再次对字符串S,P进行分析,发现P字符串中P[0]与P[1...3]都不相同,而在第5次匹配时,前4次匹配都已成功,即P[0...3]==S[0...3].回溯后令i=1;j=0,即判断S[1]与P[0]的匹配情况.而在上一次匹配过程中根据P[0...3]==S[0...3]可以得出S[1]==P[1]和P字符串本身的性质得出S[1]!=P[0].说明我们再次对S[1]与P[0]
进行判断是多余的.进一步可以推导出S[1...3]与P[0]进行判断都是多余的.

我们可以直接进行S[4]与P[0]的判断.

一般情况下如何消除这些多余的判断呢?

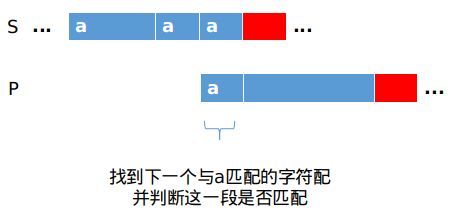
现在假设S字符串与P字符串匹配失败,如下图所示,蓝色区域表示匹配成功的区域,红色区域表示匹配失败.

匹配失败后在蓝色区域找到第一个与a匹配的字符,如图所示.蓝色区域之间的字符都不能与a字符匹配,是多余的判断故而直接忽略.

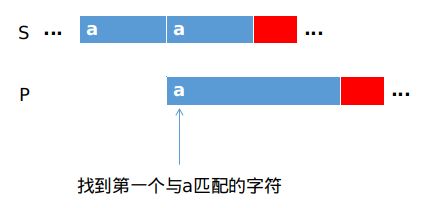
下面继续判断S字符串与P字符串的匹配情况,若匹配失败,又将继续找到下一个与a匹配的字符.

若不匹配

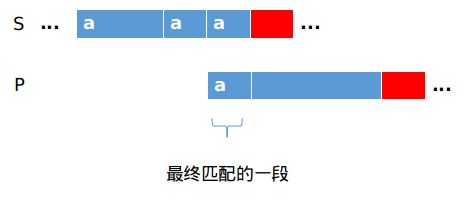
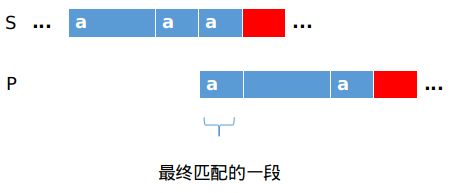
最终找到匹配的一段如图.

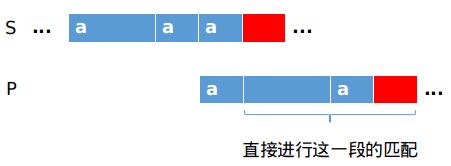
若段蓝色区域都找不到下一个与a匹配的字符,则跳过这段区域,进行下面的匹配

下面进行这段分析的总结:

最终匹配成功时,S字符串蓝色区域最后存在一段后缀与P字符串蓝色区域的一段前缀相同,而S字符串的蓝色区域与P字符串的蓝色区域相同,故P字符串蓝色区域存在一段后缀与前缀相同.且这段公共前后缀是最长的.

最终:在P字符串蓝色区域存在一段前缀与后缀相同时,可以直接忽略掉这段字符串的匹配而直接进行剩余部分的匹配

不存在相同的前后缀时,把边界当做相同的前后缀,同样进行剩余部分的匹配

在发生不匹配时,S字符串的第i个位置始终没有改变,改变的只是P字符串匹配的第j个位置,j值变化后的取值取决于第j个位置之前的字符串的最长的公共前后缀的长度.因此如果提前记录好P字符串每个位置的字符在发生不匹配时j值改变值,在匹配时即可消除掉因回溯而产生的多余的判断.在KMP中这些值组成的数组称为next数组

next数组的求法

可以使用一次遍历获得next数组,假设i表示遍历到第几个字符,j表示该字符不匹配时,应该跳转的值.即next[i]=j

• j=-1表示匹配失败时,P字符串第i个位置以及之前的字符都不能与当前S字符串中对应的字符匹配(这种情况其实只存在于i=0的时候).S字符串匹配的字符位置应加1,P字符串匹配的位置置0

• next[0]=-1,第一个字符对应的j始终为-1

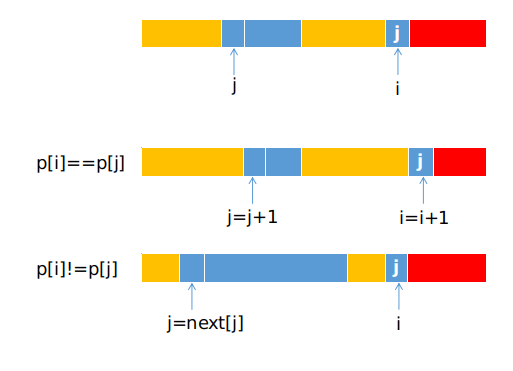
• 若p[i]==p[j]表示匹配成功,此时i++;j++;

  因为next数组是表示对应字符匹配失败时应该跳转的值,所以这里隐含一个条件,在i与j自增后p[i]!=p[j],因此增加一个判断若p[i]==p[j],设置next[i] = next[j]而不是next[i]=j;

• 若p[i]!=p[j]表示匹配失败,此时令j=next[j]继续匹配

function getNext(p){
    var i = 0;
    var j = -1;
    var next = new Array();
    next[i] = j;
    while(iif(j==-1 || p[i]==p[j]){
            i++;
            j++;
            if (p[i] != p[j])  
                next[i] = j;
            else
                next[i] = next[j];
        }else{
            j = next[j];
        }
    }
}

KMP算法匹配

function KMP(s, p){
    var next = getNext(p);
    var i = 0,
        j = 0;
    while(iif(s[i]===p[j]){
            i++;
            p++;
        }else{
            j = next[j];
        }
    }
    if(j>=p.length){
        return i-j+1;
    }else{
        return -1;
    }
}