乘法器专题研究(内含所有类型乘法器)
乘法器的verilog HDL设计汇总
1、移位相加乘法器的设计:
其大致原理如下:
从被乘数的最低位开始判断,若为1,则乘数左移i(i=0,1...(WIDTH-1))位后,与上一次和相加;若为0,则乘数左移i位后,以0相加。直至被乘数的最高位。
优点:占用的资源较少,在低速信号处理中有广泛的应用 。
缺点:串行乘法器的速度比较慢,一个结果输出需要花费多个时钟周期,在高位宽乘法运算中尤为明显。Verilog HDL代码如下:
1. //移位相加乘法器的verilog HDL代码
2. module multi_Mov_Add(a,b,outcome);
3. parameter size = 8;
4. input [size - 1 : 0] a, b; //a,b为乘法器的两个输入
5. output [2*size - 1 : 0] outcome;
6. reg [2*size - 1 : 0] outcome;
7. integer i;
8.
9. always @ (a or b)
10. begin
11. outcome = 4'b0;
12. for(i = 0; i < size; i = i + 1) //用于移位
13. begin
14. if(b[i] == 1) //如果被乘数为1,则移位相加
15. begin
16. outcome = outcome + (a<
17. end
18. end
19. end
20. endmodule
2、串行乘法器设计:
其状态图如下:
设计verilog HDL 代码如下:
1. module multi_CX(clk, x, y, result);
2.
3. input clk; //时钟信号
4. input [7:0] x, y; //x为乘数,y为被乘数
5. output [15:0] result; //运算结果
6.
7. reg [15:0] result;
8.
9. parameter s0 = 0, s1 = 1, s2 = 2; //状态
10. reg [2:0] count = 0;
11. reg [1:0] state = 0; //状态变量赋初值
12. reg [15:0] P, T; //P为运算结果的中间变量,T为乘数的中间变量
13. reg [7:0] y_reg; //y_reg为被乘数的中间变量
14.
15. always @(posedge clk) begin //时钟上升沿到达时,运行下面的语句
16. case (state) //状态S0为初始状态,从初始状态开始
17. s0: begin
18. count <= 0; //计算变量初值
19. P <= 0; //结果变量清零
20. y_reg <= y; //被乘数赋初值
21. T <= {{8{1'b0}}, x}; //乘数赋初值
22. state <= s1; //进入下一个状态
23. end
24. s1: begin //S1状态
25. if(count == 3'b111) //计数为3'b111,即7时,进入结束状态
26. state <= s2;
27. else begin //未进入结束状态
28. if(y_reg[0] == 1'b1) //被乘数末尾位为1时
29. P <= P + T; //中间结果加一次乘数
30. else //否则中间结果不变
31. P <= P;
32. y_reg <= y_reg >> 1; //被乘数右移一位,倒数第二位移到末尾
33. T <= T << 1; //乘加一次后,被乘数左移一位,这里从运算过程中可以看出
34. count <= count + 1; //count是为了统计运行一次乘法需要多少个时钟周期
35. state <= s1;
36. end
37. end
38. s2: begin
39. result <= P; //结束状态时,中间结果赋值给最终结果
40. state <= s0; //为下一次运算准备
41. end
42. default: ;
43. endcase
44. end
45.
46. endmodule
缺点:计算一次乘法需要8个周期,因此可以看出串行乘法器速度比较慢,时延大。
优点:该乘法器所占用的资源是所有类型乘法器中最少的,在低速的信号处理中有广泛的使用。
3、流水线乘法器
乘法器采用多级流水线的形式,将相邻的两个部分乘积结果再加到最终的输出乘积上,即排成一个二叉树形式的结构。(死磕下面的代码)
其verilog HDL设计如下:
1. module multi_4bits_pipelining(mul_a, mul_b, clk, rst_n, mul_out);
2.
3. input [3:0] mul_a, mul_b; //乘数与被乘数
4. input clk; //时钟信号
5. input rst_n; //复位信号
6. output [7:0] mul_out; //结果变量
7. reg [7:0] mul_out;
8. reg [7:0] stored0; //stored0,...stored3用来存逐位相乘的中间结果
9. reg [7:0] stored1;
10. reg [7:0] stored2;
11. reg [7:0] stored3;
12. reg [7:0] add01; //中间结果变量
13. reg [7:0] add23;
14. always @(posedge clk or negedge rst_n) begin
15. if(!rst_n) begin //复位信号有效
16. mul_out <= 0;
17. stored0 <= 0;
18. stored1 <= 0;
19. stored2 <= 0;
20. stored3 <= 0;
21. add01 <= 0;
22. add23 <= 0;
23. end
24. else begin
25. stored0 <= mul_b[0] ? {4'b0, mul_a} : 8'b0; //如果被乘数倒数第一位不为零,则与乘数相乘结果为{4'b0,mul_a}
26. stored1 <= mul_b[1] ? {3'b0, mul_a, 1'b0} : 8'b0; //如果被乘数倒数第二位不为零,则与乘数相乘结果为{3'b0,mul_a,1'b0}
27. stored2 <= mul_b[2] ? {2'b0, mul_a, 2'b0} : 8'b0; //同上
28. stored3 <= mul_b[3] ? {1'b0, mul_a, 3'b0} : 8'b0; //同上
29. add01 <= stored1 + stored0;
30. add23 <= stored3 + stored2;
31. mul_out <= add01 + add23; //最终结果
32. end
33. end
34. endmodule
Verilog HDL代码我都加上了注释,增加了可读性,我认为这是代码起码的尊严,也是对阅读者起码的尊重。原理就不多赘述,很简单,读懂代码即可了解。
4、Wallace树乘法器(重磅呈现)
在乘法器的设计中采用树形乘法器,可以减少关键路径和所需的加法器单元数目,Wallace树乘法器就是其中的一种。下面以一个4*4位乘法器为例介绍Wallace树乘法器及其Verilog HDL实现。
从数据最密集的地方开始,不断的反复使用全加器、半加器来覆盖“树”。全加器是一个3输入2输出的器件,因此全加器又称作3—2压缩器。通过全加器将树的深度不断缩减,最终缩减为一个深度为2的树。最后一级则采用简单的2输入加法器组成。
Wallace树乘法器的运算原理如下:
部分积 |
|||||||
被乘数 |
|
|
|
X3 |
X2 |
X1 |
X0 |
乘数 |
|
|
|
Y3 |
Y2 |
Y1 |
Y0 |
|
|
|
|
X3y0 (a[6]) |
X2y0 (a[3]) |
X1y0 (a[1]) |
X0y0 (a[0]) |
|
|
|
X3y1 (a[10]) |
X2y1 (a[7]) |
X1y1 (a[4]) |
X0y1 (a[2]) |
|
|
|
X3y2 (a[13]) |
X2y2 (a[11]) |
X1y2 (a[8]) |
X0y2 (a[5]) |
|
|
|
X3y3 (a[15]) |
X2y3 (a[14]) |
X1y3 (a[12]) |
X0y3 (a[9]) |
|
|
|
第一级 |
|||||||
|
6 |
5 |
4 |
3 |
2 |
1 |
0 |
|
X3y3 (a[15]) |
X3y2 (a[13]) |
X3y1 (a[10]) |
X3y0 (a[6]) |
X2y0 (a[3]) |
X1y0 (a[1]) |
X0y0 (a[0]) |
|
|
X2y3 (a[14]) |
X2y2 (a[11]) |
X2y1 (a[7]) |
X1y1 (a[4]) |
X0y1 (a[2]) |
|
|
|
|
X1y3 (a[12]) |
X1y2 (a[8]) |
X0y2 (a[5]) |
|
|
|
|
|
|
X0y3 (a[9]) |
|
|
|
加法器结果 |
|
|
[1 : 0] b1 |
[1 : 0] b0 |
|
|
|
对第一级的绿色部分,即a[8]和a[9],以及a[11]和a[12],使用半加器进行处理,
1. hadd U1(.x(a[8]), .y(a[9]), .out(b0)); //2输入半加器(第一级)
2. hadd U2(.x(a[11]), .y(a[12]), .out(b1));//第一级
输出分别为b0和 b1 。
第二级 |
|||||||
|
6 |
5 |
4 |
3 |
2 |
1 |
0 |
|
X3y3 (a[15]) |
X3y2 (a[13]) |
X3y1 (a[10]) |
X3y0 (a[6]) |
X2y0 (a[3]) |
X1y0 (a[1]) |
X0y0 (a[0]) |
|
|
X2y3 (a[14]) |
b1[0] |
X2y1 (a[7]) |
X1y1 (a[4]) |
X0y1 (a[2]) |
|
|
|
b1[1] |
b0[1] |
b0[0] |
X0y2 (a[5]) |
|
|
加法器结果 |
|
[1 : 0] C3 |
[1 : 0] C2 |
[1 : 0] C1 |
[1 : 0] C0 |
|
|
半加器仍然用绿色部分表示,全加器用橙色部分表示,第二级经过半加器以及全加器的处理,
即:
1. hadd U3(.x(a[4]), .y(a[5]), .out(c0)); //第二级
2. fadd U4(.x(a[6]), .y(a[7]), .z(b0[0]), .out(c1)); //3输入全加器(第二级)
3. fadd U5(.x(b1[0]), .y(a[10]), .z(b0[1]), .out(c2));
4. fadd U6(.x(a[13]), .y(a[14]), .z(b1[1]), .out(c3));
第三级 |
||||||
6 |
5 |
4 |
3 |
2 |
1 |
0 |
X3y3 (a[15]) |
C3[0] |
C2[0] |
C1[0] |
X2y0 (a[3]) |
X1y0 (a[1]) |
X0y0 (a[0]) |
C3[1] |
C2[1] |
C1[1] |
C0[1] |
C0[0] |
X0y1 (a[2]) |
|
其在verilog HDL代码中的体现如下:
1. assign add_a = {c3[1],c2[1],c1[1],c0[1],c0[0],a[2]}; //加法器(第三极)
2. assign add_b = {a[15],c3[0],c2[0],c1[0],a[3],a[1]};
3. assign add_out = add_a + add_b;
4. assign out = {add_out,a[0]};
其verilog HDL 代码如下:
1. module wallace(x,y,out);
2. parameter size = 4; //定义参数,乘法器的位数
3. input [size - 1 : 0] x,y; //输入y是乘数,x是被乘数
4. output [2*size - 1 : 0] out;
5. wire [size*size - 1 : 0] a; //a为部分积
6. wire [1 : 0] b0, b1; //第一级的输出,包含进位
7. wire [1 : 0] c0, c1, c2, c3; //第二级的输出,包含进位
8. wire [5 : 0] add_a, add_b; //第三极的输入
9. wire [6 : 0] add_out; //第三极的输出
10. wire [2*size - 1 : 0] out; //乘法器的输出(组合逻辑)
11.
12. assign a = {x[3],x[2],x[3],x[1],x[2],x[3],x[0],x[1],
13. x[2],x[3],x[0],x[1],x[2],x[0],x[1],x[0]}
14. &{y[3],y[3],y[2],y[3],y[2],y[1],y[3],y[2]
15. ,y[1],y[0],y[2],y[1],y[0],y[1],y[0],y[0]}; //部分积
16.
17. hadd U1(.x(a[8]), .y(a[9]), .out(b0)); //2输入半加器(第一级)
18. hadd U2(.x(a[11]), .y(a[12]), .out(b1));//第一级
19. hadd U3(.x(a[4]), .y(a[5]), .out(c0)); //第二级
20.
21. fadd U4(.x(a[6]), .y(a[7]), .z(b0[0]), .out(c1)); //3输入全加器(第二级)
22. fadd U5(.x(b1[0]), .y(a[10]), .z(b0[1]), .out(c2));
23. fadd U6(.x(a[13]), .y(a[14]), .z(b1[1]), .out(c3));
24.
25.
26. assign add_a = {c3[1],c2[1],c1[1],c0[1],c0[0],a[2]}; //加法器(第三极)
27. assign add_b = {a[15],c3[0],c2[0],c1[0],a[3],a[1]};
28. assign add_out = add_a + add_b;
29. assign out = {add_out,a[0]};
30.
31. endmodule
32.
33. //全加器模块
34. module fadd(x, y, z, out);
35. input x, y, z;
36. output [1 : 0] out;
37. assign out = x + y + z;
38. endmodule
39.
40. //半加器模块
41. module hadd(x, y, out);
42. input x, y;
43. output [1 : 0] out;
44. assign out = x + y;
45. endmodule
测试文件:
1. //测试文件
2.
3. `timescale 1ns/1ps
4. module wallace_tb;
5. reg [3 : 0] x, y;
6. wire [7 : 0] out;
7. wallace U1(.x(x), .y(y), .out(out)); //模块实例
8.
9. initial
10. begin
11. x = 3;
12. y = 4;
13. # 20
14. x = 2;
15. y = 3;
16. # 20
17. x = 6;
18. y = 8;
19. end
20.
21. endmodule
Moldesim中波形图如下:
5、复数乘法器
在wallace乘法器的基础上设计一个复数乘法器,复数的乘法算法是:设复数x = a + b i, y = c + d i, 则复数相乘的结果为:x * y = (a + b i)*(c + d i) = (ac - bd) + i (ad + bc) .
十分简单,只需要把部分积算出来然后就是加减运算了。
其verilog HDL代码如下:
1. //复数乘法器的verilog HDL代码
2.
3. module complex(a, b, c, d, out_real, out_im);
4. input [3:0] a, b, c, d;
5. output [8:0] out_real,out_im;
6. wire [7:0] sub1, sub2, add1, add2;
7.
8. wallace U1(.x(a), .y(c), .out(sub1));
9. wallace U2(.x(b), .y(d), .out(sub2));
10. wallace U3(.x(a), .y(d), .out(add1));
11. wallace U4(.x(b), .y(c), .out(add2));
12.
13. assign out_real = sub1 - sub2;
14. assign out_im = add1 + add2;
15. endmodule
16. //下面是wallace树乘法器模块
17. module wallace(x,y,out);
18. parameter size = 4; //定义参数,乘法器的位数
19. input [size - 1 : 0] x,y; //输入y是乘数,x是被乘数
20. output [2*size - 1 : 0] out;
21. wire [size*size - 1 : 0] a; //a为部分积
22. wire [1 : 0] b0, b1; //第一级的输出,包含进位
23. wire [1 : 0] c0, c1, c2, c3; //第二级的输出,包含进位
24. wire [5 : 0] add_a, add_b; //第三极的输入
25. wire [6 : 0] add_out; //第三极的输出
26. wire [2*size - 1 : 0] out; //乘法器的输出(组合逻辑)
27.
28. assign a = {x[3],x[2],x[3],x[1],x[2],x[3],x[0],x[1],
29. x[2],x[3],x[0],x[1],x[2],x[0],x[1],x[0]}
30. &{y[3],y[3],y[2],y[3],y[2],y[1],y[3],y[2]
31. ,y[1],y[0],y[2],y[1],y[0],y[1],y[0],y[0]}; //部分积
32. hadd U1(.x(a[8]), .y(a[9]), .out(b0)); //2输入半加器(第一级)
33. hadd U2(.x(a[11]), .y(a[12]), .out(b1));//第一级
34. hadd U3(.x(a[4]), .y(a[5]), .out(c0)); //第二级
35.
36. fadd U4(.x(a[6]), .y(a[7]), .z(b0[0]), .out(c1)); //3输入全加器(第二级)
37. fadd U5(.x(b1[0]), .y(a[10]), .z(b0[1]), .out(c2));
38. fadd U6(.x(a[13]), .y(a[14]), .z(b1[1]), .out(c3));
39.
40.
41. assign add_a = {c3[1],c2[1],c1[1],c0[1],c0[0],a[2]}; //加法器(第三极)
42. assign add_b = {a[15],c3[0],c2[0],c1[0],a[3],a[1]};
43. assign add_out = add_a + add_b;
44. assign out = {add_out,a[0]};
45.
46. endmodule
47.
48. //全加器模块
49. module fadd(x, y, z, out);
50. input x, y, z;
51. output [1 : 0] out;
52. assign out = x + y + z;
53. endmodule
54.
55. //半加器模块
56. module hadd(x, y, out);
57. input x, y;
58. output [1 : 0] out;
59. assign out = x + y;
60. endmodule
测试文件代码如下:
1. //复数乘法器测试文件
2.
3. `timescale 1ns/1ps
4. module complex_tb;
5. reg [3:0] a, b, c, d;
6. wire [8:0] out_real;
7. wire [8:0] out_im;
8. complex U1(.a(a), .b(b), .c(c), .d(d), .out_real(out_real),
9. .out_im(out_im));
10.
11. initial
12. begin
13. a = 2; b = 2; c = 5; d = 4;
14. #10
15. a = 4; b = 3; c = 2; d = 1;
16. #10
17. a = 3; b = 2; c = 3; d = 4;
18. end
19.
20. endmodule
ModelSim中仿真波形截图如下:
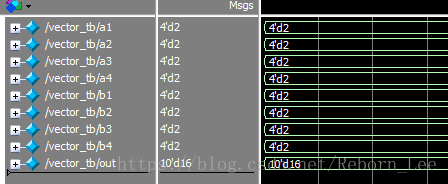
6、向量乘法器
同样基于Wallace树乘法器,我们来构造向量乘法器。
在一些矩阵运算中经常用到向量的相乘运算,本例以4维向量为例子介绍向量乘法器的verilog HDL设计。
设向量
a = (a1, a2, a3, a4),
b = (b1, b2, b3, b4),
则a 与 b的点乘为:
a * b = a1 b1 + a2 b2 + a3 b3 + a4 b4,
即向量对应位置的值相乘,再相加。原理十分简单,下面给出verilog HDL设计代码:
1. //向量乘法器的设计
2. module vector(a1, a2, a3, a4, b1, b2, b3, b4, out);
3. input [3:0] a1, a2, a3, a4;
4. input [3:0] b1, b2, b3, b4;
5. output [9:0] out; //a1b1+a2b2+a3b3+a4b4为10位
6. wire [7:0] out1, out2, out3, out4;//乘积项a1b1为8位,a2b2,a3b3,a4b4同理为8位
7. wire [8:0] out5, out6 ;//同理a3b3+a4b4为9位,a1b1+a2b2为9位
8. wire [9:0] out; //a1b1+a2b2+a3b3+a4b4为10位
9.
10. //wallace树乘法器例化部分,得到乘积项
11. wallace m1(.x(a1), .y(b1), .out(out1)); //out1 == a1b1
12. wallace m2(.x(a2), .y(b2), .out(out2)); //out2 == a2b2
13. wallace m3(.x(a3), .y(b3), .out(out3)); //out3 == a3b3
14. wallace m4(.x(a4), .y(b4), .out(out4)); //out4 == a4b4
15.
16. assign out5 = out1 + out2; //a1b1+a2b2
17. assign out6 = out3 + out4; //a3b3+a4b4
18. assign out = out5 + out6; //a1b1+a2b2+a3b3+a4b4
19.
20. endmodule
21.
22. //wallace树乘法器模块
23. module wallace(x,y,out);
24. parameter size = 4; //定义参数,乘法器的位数
25. input [size - 1 : 0] x,y; //输入y是乘数,x是被乘数
26. output [2*size - 1 : 0] out;
27. wire [size*size - 1 : 0] a; //a为部分积
28. wire [1 : 0] b0, b1; //第一级的输出,包含进位
29. wire [1 : 0] c0, c1, c2, c3; //第二级的输出,包含进位
30. wire [5 : 0] add_a, add_b; //第三极的输入
31. wire [6 : 0] add_out; //第三极的输出
32. wire [2*size - 1 : 0] out; //乘法器的输出(组合逻辑)
33.
34. assign a = {x[3],x[2],x[3],x[1],x[2],x[3],x[0],x[1],
35. x[2],x[3],x[0],x[1],x[2],x[0],x[1],x[0]}
36. &{y[3],y[3],y[2],y[3],y[2],y[1],y[3],y[2]
37. ,y[1],y[0],y[2],y[1],y[0],y[1],y[0],y[0]}; //部分积
38. hadd U1(.x(a[8]), .y(a[9]), .out(b0)); //2输入半加器(第一级)
39. hadd U2(.x(a[11]), .y(a[12]), .out(b1));//第一级
40. hadd U3(.x(a[4]), .y(a[5]), .out(c0)); //第二级
41.
42. fadd U4(.x(a[6]), .y(a[7]), .z(b0[0]), .out(c1)); //3输入全加器(第二级)
43. fadd U5(.x(b1[0]), .y(a[10]), .z(b0[1]), .out(c2));
44. fadd U6(.x(a[13]), .y(a[14]), .z(b1[1]), .out(c3));
45.
46.
47. assign add_a = {c3[1],c2[1],c1[1],c0[1],c0[0],a[2]}; //加法器(第三极)
48. assign add_b = {a[15],c3[0],c2[0],c1[0],a[3],a[1]};
49. assign add_out = add_a + add_b;
50. assign out = {add_out,a[0]};
51.
52. endmodule
53.
54. //全加器模块
55. module fadd(x, y, z, out);
56. input x, y, z;
57. output [1 : 0] out;
58. assign out = x + y + z;
59. endmodule
60.
61. //半加器模块
62. module hadd(x, y, out);
63. input x, y;
64. output [1 : 0] out;
65. assign out = x + y;
66. endmodule
其测试文件如下:
1. //向量乘法器测试文件
2. `timescale 1ns/1ps
3. module vector_tb;
4. reg [3:0] a1, a2, a3, a4;
5. reg [3:0] b1, b2, b3, b4;
6. wire [9:0] out;
7. initial
8. begin
9. a1 = 2'b10; a2 = 2'b10; a3 = 2'b10; a4 = 2'b10;
10. b1 = 2'b10; b2 = 2'b10; b3 = 2'b10; b4 = 2'b10;
11. end
12.
13. vector U1(.a1(a1), .a2(a2), .a3(a3), .a4(a4), .b1(b1),
14. .b2(b2), .b3(b3), .b4(b4), .out(out));
15.
16. endmodule
在modelsim中仿真波形如下:
7、查找表乘法器
查找表乘法器就是将乘积放在存储器中,将操作数作为地址访问存储器,得到的输出结果就是乘法器的运算结果。这种乘法器的运算速度就等于所使用的存储器的速度,一般用于较小规模的乘法器。
例如实现一个2*2位的乘法器,其查找表如下表所示:
multiple |
00(0) |
01(1) |
10(2) |
11(3) |
00(0) |
0000 |
0000 |
0000 |
0000 |
01(1) |
0000 |
0001 |
0010 |
0011 |
10(2) |
0000 |
0010 |
0100 |
0110 |
11(3) |
0000 |
0011 |
0110 |
1001 |
但是当乘法器的位数提高时,例如要实现一个8*8位的乘法器就需要2^(8+8) * 16个存储单元(2^8代表2^8个数,16代表每个乘积项有16位,总共有2^8 * 2^8个乘积项),显然这需要一个很大的存储器。那块如何能兼顾速度和资源呢?可以考虑用部分积技术。可以分别计算每一位或者每两位相乘的结果,再将结果进行移位相加,就得到了最终的结果。(至于,如何移位,移几位,我后面会仔细解释)。这种方法可以大幅度地降低查找表的规模。
下面用查找表的思想设计一个4位乘法器。(用2位乘法器查找表实现4位乘法器查找表,降低查找表的规模)。
其verilog HDL设计代码为:
1. //4位查找表乘法器verilog HDL设计
2.
3. module lookup_mult(a, b, clk, out);
4. input [3:0] a, b; //4位输入
5. input clk;
6. output [7:0] out; //8位输出
7. reg [7:0] out;
8.
9. reg [1:0] firsta, firstb, seconda, secondb; //a的高两位为firsta,低两位为seconda,b同理
10. wire [3:0] outa, outb, outc, outd; //看例化部分
11.
12. always @ (posedge clk)
13. begin
14. firsta <= a[3:2];
15. seconda <= a[1:0];
16. firstb <= b[3:2];
17. secondb <= b[1:0];
18. end
19. //例化部分
20. lookup m1(.out(outa), .a(firsta), .b(firstb), .clk(clk));
21. lookup m2(.out(outb), .a(firsta), .b(secondb), .clk(clk));
22. lookup m3(.out(outc), .a(seconda), .b(firstb), .clk(clk));
23. lookup m4(.out(outd), .a(seconda), .b(secondb), .clk(clk));
24.
25. always @ (posedge clk)
26. begin
27. out <= (outa<<4) + (outb<<2) + (outc<<2) +outd; //乘法器的输出结果
28. end
29.
30. endmodule
31.
32. //2位查找表
33. module lookup(out, a, b, clk);
34. output [3:0] out;
35. input [1:0] a, b; //2位输入
36. input clk;
37. reg [3:0] out; //4位输出
38. reg [3:0] address;//地址,例如a*b,则地址为{a,b}
39.
40. always @ (posedge clk)
41. begin
42. address <= {a,b}; //用操作数的拼接作为地址访问存储器
43. case(address)
44. 4'b0000: out <= 4'b0000;
45. 4'b0001: out <= 4'b0000;
46. 4'b0010: out <= 4'b0000;
47. 4'b0011: out <= 4'b0000;
48. 4'b0100: out <= 4'b0000;
49. 4'b0101: out <= 4'b0001;
50. 4'b0110: out <= 4'b0010;
51. 4'b0111: out <= 4'b0011;
52. 4'b1000: out <= 4'b0000;
53. 4'b1001: out <= 4'b0010;
54. 4'b1010: out <= 4'b0100;
55. 4'b1011: out <= 4'b0110;
56. 4'b1100: out <= 4'b0000;
57. 4'b1101: out <= 4'b0011;
58. 4'b1110: out <= 4'b0110;
59. 4'b1111: out <= 4'b1001;
60. default: out<= 4'bx;
61. endcase
62. end
63.
64. endmodule
测试代码为:
1. //测试文件
2. `timescale 1ns/1ps
3. module lookup_mult_tb;
4. reg [3:0] a,b;
5. reg clk = 0;
6. wire [7:0] out;
7. integer i,j;
8. always #10 clk = ~clk;
9. lookup_mult U1(.out(out), .a(a), .b(b), .clk(clk));
10.
11. initial
12. begin
13. a = 0;
14. b = 0;
15. for(i = 1; i < 15; i = i + 1)
16. #20 a = i;
17. end
18.
19. initial
20. begin
21. for(j = 1; j < 15; j = j + 1)
22. #20 b = j;
23. end
24.
25. initial
26. begin
27. #360 $stop;
28. end
29.
30. endmodule
重点语句解释:
1. out <= (outa<<4) + (outb<<2) + (outc<<2) +outd;
部分积 |
|||||||
[3:0] a |
|
|
|
X3 |
X2 |
X1 |
X0 |
[3:0] b |
|
|
|
Y3 |
Y2 |
Y1 |
Y0 |
|
|
|
|
X3y0
|
X2y0
|
X1y0
|
X0y0
|
|
|
|
X3y1 |
X2y1
|
X1y1
|
X0y1
|
|
|
|
X3y2 |
X2y2 |
X1y2
|
X0y2
|
|
|
|
X3y3 |
X2y3 |
X1y3 |
X0y3
|
|
|
|
注意:
1. always @ (posedge clk)
2. begin
3. firsta <= a[3:2];
4. seconda <= a[1:0];
5. firstb <= b[3:2];
6. secondb <= b[1:0];
7. end
由上述代码可以知道,a的高2位为firsta,在上述表格中用黄色代替,低2位为seconda,用红色代替,同理b的高2位为firstb,用蓝色代替,低2位为secondb,用绿色代替。
1. lookup m1(.out(outa), .a(firsta), .b(firstb), .clk(clk));
2. lookup m2(.out(outb), .a(firsta), .b(secondb), .clk(clk));
3. lookup m3(.out(outc), .a(seconda), .b(firstb), .clk(clk));
4. lookup m4(.out(outd), .a(seconda), .b(secondb), .clk(clk));
有此四段代码可知,firsta与firstb相乘得到outa,在上表中的体现用紫色字体代替;同理,seconda与secondb相乘得outd,用红色字体表示;其他就不一一赘述,可见若用2位移位相加法求最终的乘法输出out,outa需要左移4位才能到表上紫色字体的位置,即firsta与firstb用查表法相乘的结果为0000_outa,”_”表示分隔符,没有任何其他意义,需要左移4位才能得到outa_0000,即紫色字体在表格中的位置。
仔细看我的分析应该就能明白上述意思,并且能够推理出为什么outb,outc左移2位,最后由如下代码得出结果:
1. out <= (outa<<4) + (outb<<2) + (outc<<2) +outd;