信道编码之差错控制原理

在前面讲差错控制方式时，有的编码只能检错，却不能纠错；有的码既能检错，又能纠错。这个到底是由什么决定的呢？

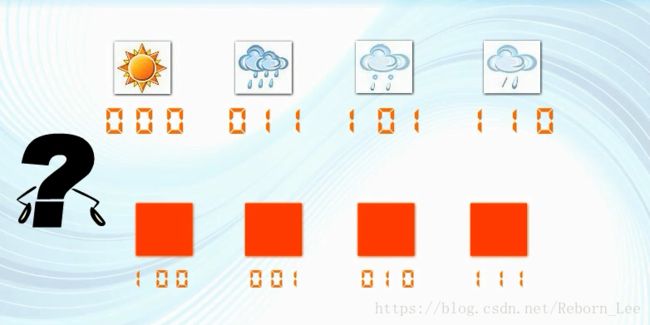
通过一个简单的例子来说明这个问题。我们知道，一个由3位二进制数字构成的码组，总共由8种不同的组合。若将其全部表示天气，则可以表示8种不同的天气，如下：

若其中任一码组在传输中发生一个或多个错码，会发生什么情况呢？

就变成另一个信息码组了，比如说000变成了011，接收端就会将晴天误判为雨天了。

这时接收端是无法发现错误的。

如果在这8种码组中只准使用4种来传送信息，比如：

这时就会有3中情况。比如说码组000，如果000中错了1位，则接收端就可能会接收到100、010、或001。

这3种码组都是不允许使用的，因此接收端就可以认为发现了错码；

但如果000错了2位，接收端就可能收到110、011或101，是允许使用的码组，这样接收端就会产生误判，不会发现错误；

如果3位都错的话，也是不允许使用的码组，因此接收端可以判断出码组是有错误的。

综上，如果接收端收到了禁用码组，即不可用的码组，就可以认为发现了错码。

但要注意的是，虽然发现了错码，但并不知道传输过程中到底是那个码发生了错误，发生了几个错误。

例如说，接收端接收到了100码，虽然是禁用码组，但我们是不知道是000、101、110哪个发生了1个错误造成的，还是011发生3位错误造成的，因此只能发现错误，却不能纠正错误。

那什么样的码可以纠错呢？

我们可以把这个例子中可用的码组再缩小范围。

比如说只用000表示晴天，111表示雨天。其余的码组都是禁用码组，这时如果接收端接收到了001，就可以判断出现了错误，如果认为只发生了一个错误，那么接收端就知道是000发生了错误，因为111发生1位错误是无论如何都变不成001的，从而将001纠正为000.

但如果认为错误码数不超过两个，那么000错一位和111错两位都可能变为001，因此就只能检错而不能纠错了。

到底错几个码我们如何得知呢？如果错了2位码，却按照1位码来纠错，那不就还是会引起错误？

信道编码不是万金油，是不可能把发送端的错误都检出来或者纠正出来的。用得不好，反而会带来一些麻烦。

但从整体、平均的角度来看，它还是可以大大地改善系统的可靠性。至于一种编码它的纠错和检错能力如何，就需要找到一种规律，来说明这个能力。

这个规律如何找呢？

首先澄清几个基本概念。

分组码：

从前面的例子中，可以得出如果不要求检错和纠错，为了传输晴、雨、霜、雾4种不同的信息，只要两位码就够了，即00、01、10、11，我们称它们为信息位。

而为了检错和纠错，实际用了3位码000,011,101,110来表示四种信息，那么增加的那位就称为监督位。

我们将这种将信息码分组，为每组信码附加若干监督码的编码集合，称为分组码。

分组码一般用符号（n，k）表示，其中 k是每组二进制信息码元数，n是分组码的总位数，即分组码的长度。那么由此，可以得到监督码元数r = n - k。

刚刚的那个例子中，n，k，r各是多少？

很容易得知，n = 3，k = 2， r = 1 。

码重和码距的概念？

码重，就是在分组码中1的数目；

码距，即两个码组对应位上数字不同的位数，又称为汉明距离。

同时，我们把某种编码中各个码字间距离最小值称为最小码距。

上面例子中，4个码组之间，可以看到任意两个码组距离均为2，最小码距也为2 。

说了这么多，这些概念有什么用呢？

这些概念是为那个所谓的规律准备的，蕴藏着大智慧。

一种编码的最小码距的大小直接关系到这种编码的检错和纠错能力。（后面解释）

现在回到那个规律上，看看前人是如何找到的这种规律？

首先，为了检测e个错码，要求最小码距：

即若要求检测e个错码，最小码距d0至少不小于e+1 。

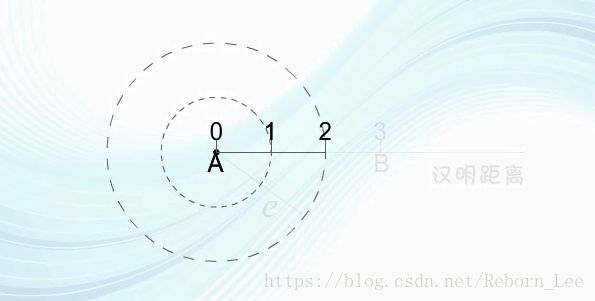
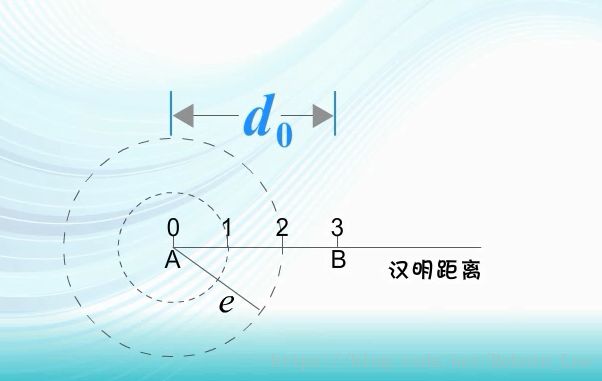
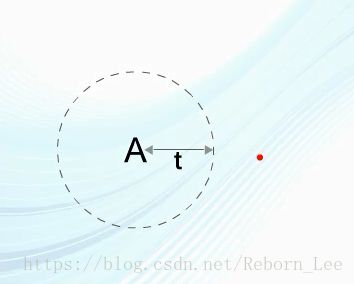
我们用下图简单说明一下，设一码组A位于0点。若码组A中发生1位错码，则可以认为A的位置将移动到以0位圆心，以1位半径的圆上某点；

若码组A中发生两位错码，则其位置不会超出以0点为圆心，以2为半径的圆。

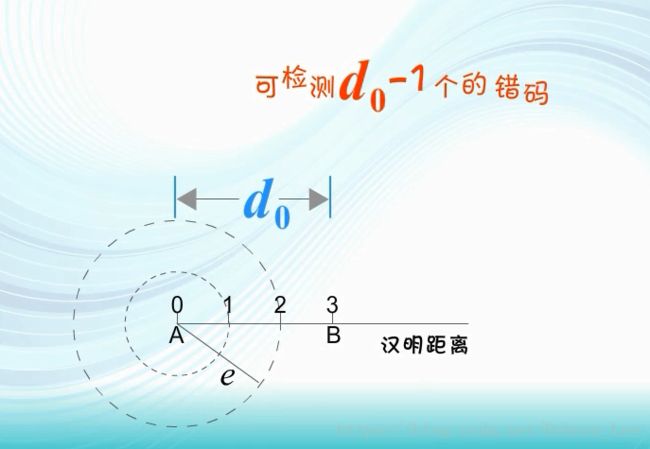
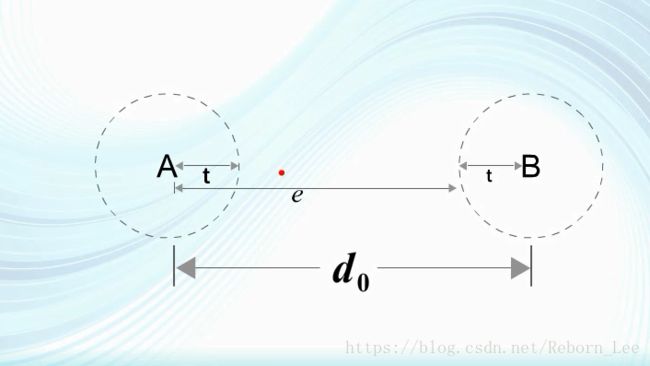
因此，只要码组A和码组B的最小码距大于等于3，则半径为2的圆上以及圆内就不会有其他的许用码组。

也就是说只要码组A和码组B的最小码距大于等于3，当码组A发生2位或2位以下错码时，就不可能移到码组B的位置上。

因而能检测2个以下的错码。

或者说，码组A发生两位及两位以下错码时，不可能变成另一任何许用码组。因而能检测错码的位数等于2 。

同理，若一种编码的最小码距为d0，则将能检测（d0 - 1）个错码。

如果以B为圆心来看，它们发生错码的可能还会有交集呢？

因为这里只是检错，只要发现码组错误就行了，而不管这个错误是离A近还是离B近，所以有交集是不要紧的。

但如果要纠错，就要考虑这个错误离A近还是离B近了，一般离谁近，就纠正为谁。所以这时候就要求错码到各自的原码的距离不能有交集，不能说我既可以纠正为A，又可以纠正为B。

最小码距和纠错能力之间是否有关系呢？

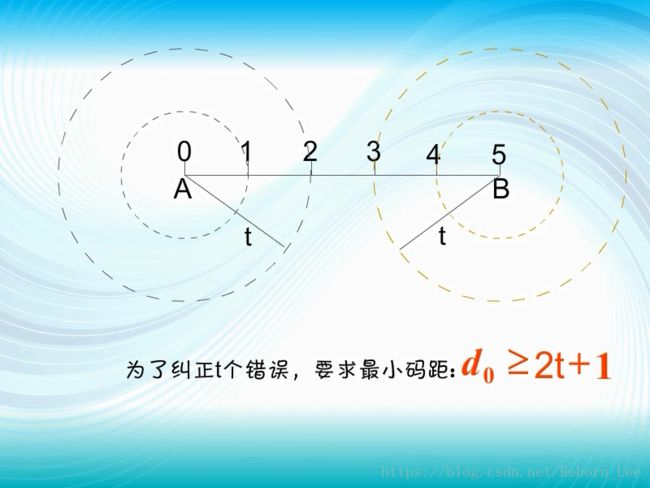
为了纠正t个错误，要求最小码距  ，

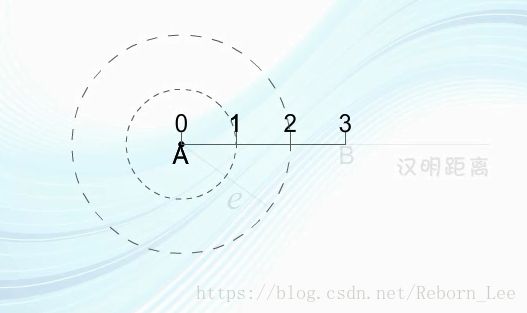
图中码组A或B若发生不多于两位错码，和它们的错码位置均不会超过以原位置为圆心，以2为半径的圆，由于这两个圆不重叠，故可以这样判决：若接收码组落在以A为圆心的圆上，就判决收到的码组为A；

若落于以B为圆心的圆上，就判决码组为B。这样就能纠正两位错码。

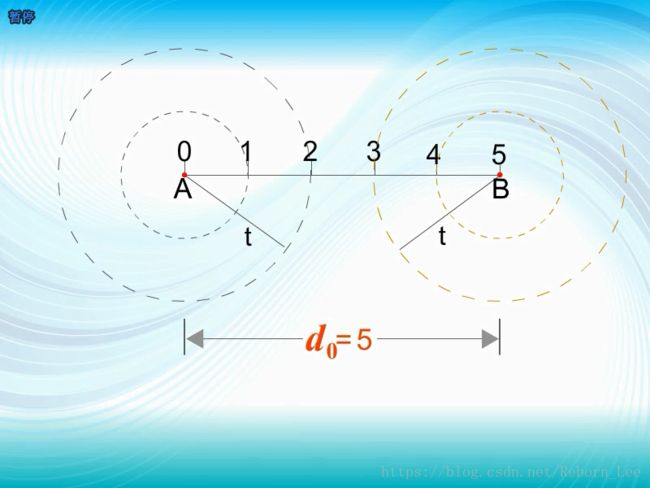
若这种编码中除码组A和B外，还有许多种不同码组，都不会相互重叠。这样，每种码组如果发生不超过两位错码都将纠正。因此，当最小码距d0=5时，能够纠正两个错误，且最多只能纠正两个错码。

若错码达到3个，就将落于另一圆上，从而发生错判。

因此，为纠正t个错误，最小码距应不小于2t+1。

那能不能纠正t个错误，并同时检测e个错码呢？

或者这样描述这个问题，d0应该满足什么条件，编码既能检错又能纠错呢？

对于一些错码数较多的码组，会超过该码的纠错能力，因此还需要检错，能自动按检错重发方式工作，以降低系统的总误码率。这就要求最小码距 ，且  。

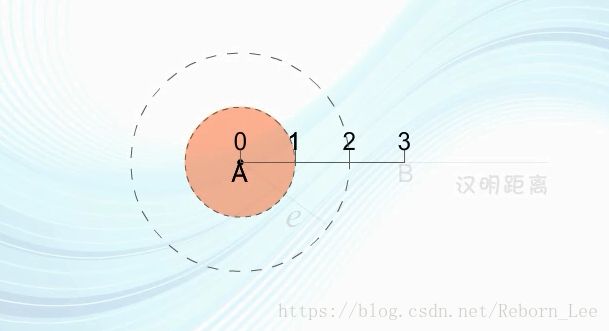
当错码落于以A 为圆心，半径大于t的圆上时，此时是没有办法纠正错误的，即e>t；

此时要想检测e个错误时，显然就要e>t，而e又要小于d0-t，否则就进入许用码组B的纠错范围内，而被错纠为B，因此就要满足

。（这段描述，想要更形象的理解要结合下图）

归纳总结：（这段总结堪称印度神油）