(JZ4252)2019.01.30【NOIP提高组】模拟B组 0.QYQ的图

【五校联考7day2】QYQ的图

Description

给你一个n个点，m条边的无向图，每个点有一个非负的权值ci，现在你需要选择一些点，使得每一个点都满足：
如果这个点没有被选择，则与它有边相连的所有点都必须被选择。
问：满足上述条件的点集中，所有选择的点的权值和最小是多少？
QYQ很快就解决了这个问题，但是他已经回到了左下角……没有留下答案，现在只好请你来解决这个问题啦！

Input

从文件graph.in中输入数据。
输入的第一行包含两个整数n，m
输入的第二行包含n个整数，其中第i个整数代表ci
输入的第三行到第m+2行，每行包含两个整数u，v，代表点u和点v之间有一条边

Output

输出到文件graph.out中。
输出的第一行包含一个整数，代表最小的权值和

Sample Input
3 1
1 2 3
3 1

Sample Output
1
样例说明：
只选择1号点，满足题意

Data Constraint

对于20% 的数据：n<=10
对于40%的数据：n<=20
对于100%的数据：1<=n<=50， 1<=m<=500， 0<=c<=1000
图中可能会有重边，自环。
点的编号为1—n。

纪中题解：

直接搜索就好了，当然不要 O(2^n)那种，每次搜索的时候如果这个点不选，就直接把与它相连的所有点选上，搜索的时候加入一些剪枝，比如如果现在的结果已经比现在的最佳答案大了就直接不搜了

悲催的故事：

   原本是想直接打个暴搜，dfs选的点。那么就反推题目(如果这个点没有被选择，则与它有边相连的所有点都必须被选择)：如果这个点被选择，则与它有边相连的所有点都不被选择。因为这样代价最小。
   过了水样例，但后来发现，如下图：肯定要选权值为二的那个点，但如果按之前的方法来算，那么3–10就会选10，3–5就选不了了

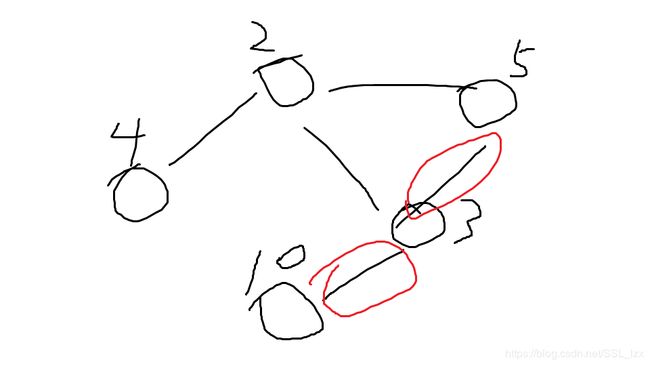
   然后就想着dfs不选的数。每不选一个数，就将与它有边相连的点加上。我们设k数组来装可以dfs的点，不可以的点包括：之前dfs过的点，加上的点。然后再dfs。
   不过不知道是回溯出了问题还是怎么的，只有20分╮(╯▽╰)╭（不过你也没有判断自环和重边啊！(○･｀Д´･ ○)）

20%：

#include
#include
#include
#include
#include
using namespace std;
int n,m,ans=233333,minn;
int c[55];
bool p[55][55],d[55][55],k[55];

void dfs(int x){
bool e[55][55];
	k[x]=0;
	if (minn>=ans) return;
	memcpy(e,p,sizeof(p));
	for (int i=1; i<=n; i++) if (p[x][i]){
		minn+=c[i];
		k[i]=0; 
		p[x][i]=0; p[i][x]=0;
		for (int j=1; j<=n; j++) {p[i][j]=0; p[j][i]=0;}
	}
	for (int i=1; i<=n; i++) if (k[i]) dfs(i); 
	memcpy(p,e,sizeof(e));
	k[x]=1;
}
int main(){
    freopen("graph.in","r",stdin);
    freopen("graph.out","w",stdout);
    
	scanf("%d%d",&n,&m);
	for (int i=1; i<=n; i++) scanf("%d",&c[i]);
	for (int i=1; i<=m; i++){
		int u,v;
		scanf("%d%d",&u,&v);
		p[u][v]=1; p[v][u]=1;
	}
	memcpy(d,p,sizeof(d));
	for (int i=1; i<=n; i++) {
		minn=0;
		memcpy(p,d,sizeof(p)); 
		memset(k,1,sizeof(k));
		dfs(i);
		ans=min(ans,minn);
	}
	printf("%d",ans);
	return 0;

	fclose(stdin); fclose(stdout);
}

   
   
   

100%

#include
#include
#include
#include
#include
using namespace std;
struct node{
	int to,next;
}a[1100];
int n,m,tot,ans,minn;
int b[55],c[55],ls[55],jh[55];
bool k[55],bj[55];

void add(int x,int y){
	a[++tot].to=y;
	a[tot].next=ls[x];
	ls[x]=tot;
}

void dfs(int x){
	b[++tot]=x; k[x]=1;
	for (int i=ls[x]; i; i=a[i].next)
		if (!k[a[i].to]) dfs(a[i].to);
}
void QYQ(int dep,int z){
	if(z>=minn) return;//剪枝
	if(dep>tot){
		minn=min(minn,z);
		return;
	}
	QYQ(dep+1,z+c[b[dep]]);
	if(!jh[b[dep]]&&!bj[b[dep]]){
		for(int i=ls[b[dep]]; i; i=a[i].next) jh[a[i].to]++;
		QYQ(dep+1,z);
		for(int i=ls[b[dep]]; i; i=a[i].next) jh[a[i].to]--;
	}
}
int main(){
    freopen("graph.in","r",stdin);
    freopen("graph.out","w",stdout);
    
	scanf("%d%d",&n,&m);
	for (int i=1; i<=n; i++) scanf("%d",&c[i]);
	for (int i=1; i<=m; i++){
		int u,v;
		scanf("%d%d",&u,&v);
		add(u,v); add(v,u);
		if (u==v) bj[u]=1;
	}
	for (int i=1; i<=n; i++) {
		minn=233333333; tot=0;
		if (k[i]) continue;
		dfs(i);
		QYQ(1,0);
		ans+=minn;
	}
	printf("%d",ans);
	return 0;

	fclose(stdin); fclose(stdout);
}