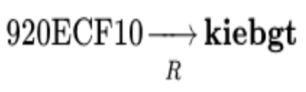深入浅出彩虹表原理

什么是彩虹表？

        一言以蔽之，彩虹表是一种破解用户密码的辅助工具。彩虹表以时空折中理论为基础，但并不是简单地“以空间换时间”，而是一种“双向交易”，在二者之间达到平衡。1980年，公钥密码学的提出者之一Hellman针对DES算法（一种对称加密算法）提出了一种时空折中算法，即彩虹表的前身：预先计算的散列链集。2003年瑞典的Philippe Oechslin在其论文Making a Faster Cryptanalytic Time-Memory Trade-Off（参考博客2）中对Hellman的算法进行了改进，并命名为彩虹表。当时是针对Windows Xp开机认证的LM散列算法。当然，目前除了破解开机密码，彩虹表目前还能用于SHA、MD4、MD5等散列算法的破译，速度快、破解率高，正如Philippe在论文中提到的：“1.4G的彩虹表可以在13.6s内破解99.9%的数字字母混合型的Windows密码“。实际上，Philippe所做的改进本质上是减少了散列链集中可能存在的重复链，从而使空间的有效利用率更高，关于这一点，后面会详述。

        为了便于叙述，本文以MD5为示例（实际应用中，不推荐使用MD5，而推荐SHA256, SHA512, RipeMD, WHIRLPOOL等），即以MD5作为明文的散列算法H，加密后的密文为q，明文为p。彩虹表的作用就是在已知散列算法H和散列后的密文q的情况下，快速地得到明文p。除了MD5，参考博客3中还给出了针对LM、NTLM和SHA1等算法对应的彩虹表。整个破解过程为：根据密文q所使用的散列算法H，生成或者下载针对该算法的彩虹表，然后再基于彩虹表对密文进行破解，最终得到明文p。

不可逆的散列算法（HASH）

        哈希（Hash）算法就是单向散列算法，它把某个较大的集合P映射到另一个较小的集合Q中，假如这个算法叫H，那么就有Q = H（P）。对于P中任何一个值p都有唯一确定的q与之对应，但是一个q可以对应多个p。作为一个有用的Hash算法，H还应该满足：H(p)速度比较快； 给出一个q，很难算出一个p满足q = H(p)；给出一个p1，很难算出一个不等于p1的p2使得 H(p1)=H(p2)。  

        MD5是一种常见的散列算法。由参考博客5可知，本质上，MD5是将明文对应的二进制值与四个特定的32位的二进制值进行多轮的与、或、非、异或等运算，最终将明文对应的二进制转换成新的二进制。由于运算过程中存在进位丢失，导致人们无法根据MD5的计算过程和最终结果逆向计算出对应的明文。

        这里还想补充的一点是：MD5常常和Base64编码一起使用。原因是：MD5的输入是明文对应的二进制，输出也是二进制，但输出的二进制无法保证还能解析成可打印字符（以ASCII码为例，其第0～32号及第127号是控制字符或通讯专用字符，不便于打印/显示/存储），而Base64恰好是一种网络上最常见的基于64个可打印字符来表示二进制数据的方法。以下分析都默认执行了Base64的转换。

彩虹表的前身：预先计算的散列链

        由前面的描述已知，由于MD5具有不可逆性，因而即使我们知道了加密算法H和加密后的密文q，我们也无法找到一个反函数R，使得p=R(q)=R(H(p))。因而本文介绍的所有破解算法（包括彩虹表）本质上都属于穷举法。

穷举法

        为了根据H和q获取p，我们首先想到了最简单的穷举法。假设p字符集为alpha-numeric（参考博客4，即p由数字和字母组成），穷举法就是穷举所有的字母和数字的组合，依次执行H运算，并将运算结果和q进行比较：如果不相同则继续寻找下一个；如果相同，则由于MD5不保证H(p1)=H(p2)一定不存在（概率极低），因而此时极大概率获取到的就是明文。显然，随着明文字符集的扩充（比如包括!@#$%等特殊符号）和密码长度的增加，穷举法的破解耗时之长，可想而知。参考博客6中就提到：以14位字母和数字的组合密码为例，共有1.24×10^25种可能，即使电脑每秒钟能进行10亿次运算，也需要4亿年才能破解。

字典表

        为了解决穷举法耗时长的问题，于是有了字典表，该方法就是事先将字符集中所有可能的组合执行H运算，并将明文及其对应的运算结果以（明文，密文）对儿的方式存储起来。执行破解时通过查询字典表的方式，匹配密文的明文即为需要破解的密码。还是以14位字母和数字的组合密码为例，生成的密码32位哈希串的对照表将占用5.7×10^14 TB的存储空间。如果增加密码长度或添加符号，需要的时间或磁盘空间将更加难以想象。

预先计算的散列链集

        为了解决字典法对海量磁盘空间的要求，1980年，Hellman想出了一种以计算时间降低存储空间的办法，即预先计算的散列链。理解散列链集为何能降低对磁盘空间要求的关键是理解约简函数（reduction function）R，该函数的定义域和值域恰好和散列函数H相反，即通过该函数可以将哈希值约简为与原明文相同定义域（字符集）的值。前面已经讲过，在已知散列函数H和密文q的情况下，是不可能找到反函数R，使得p=R(q)=R(H(p))的。所以这里的约简函数R不是反函数，而是一种将散列函数H的值域映射回其定义域的函数。例如六位的明文aaaaaa执行H运算后为“281DAF40”，而对“281DAF40”进行R运算后得到另一个六位字母格式的值“sgfnyd”。因为这个值在H函数的定义域中，因此可以对它继续进行H运算。就这样，将H运算、R运算、H运算......这个过程反复地重复下去，重复一个特定的次数k以后，就得到一条哈希链，例如k为2时得到如下哈希链：

        这条链并不需要完整地保存下来，我们只需要保存起始节点和末节点即可，例如上例中只需要保存（aaaaaa，kiebgt）对儿即可，因为中间的值都可以通过计算得出。和字典法相对比可知，这个链条实际上包含了两个“（明文，密文）”对儿，即（aaaaaa，281DAF40）和（sgfnyd，920ECF10）。也就是说，原本需要存储两个对儿的数据，通过哈希链，就只需要存储一个对儿即可，空间利用率提升了一倍。试想一下，如果继续增大k值，就意味着由这条哈希链的起始节点和末节点组成的（明文，密文）对儿所能计算出的（明文，密文）对儿将更多。反过来可以说，同样大小的空间，如果存储散列集对儿，将比存储普通的字典对儿所能涵盖的（明文，密文）对儿多很多。这才是约简函数R存在的核心价值。至此我们可以发现，字典法不就是散列链集当k等于1时的特殊情况吗？当为1时的链为aaaaaa->281DAF40->sgfnyd，此时由于链条中只包含一个（明文，密文）对儿，散列链集自然就退化为字典表。

        以大量随机明文作为起始节点，通过上述步骤计算出哈希链，并同样将起始明文和末节点值存储起来，即可得到一张哈希链集。如下示例：

......

这张链集要如何使用呢？例如，假如我们要破解已知的密文为920ECF10，首先对其执行一次R运算，得到“kiebgt”：

        恰巧在本例中，它等于集合中的一个末节点，因此我们可以猜测明文有极大可能存在于以起始节点aaaaaa开头，kiebgt结尾的这条链中（前面也提到过，因为函数H和R都有可能发生碰撞，即从不同的输入得到相同输出，因而可能性并非100%）。为了进一步验证，我们从起始节点开始重建哈希链：

        算到这里我们发现，sgfnyd进行哈希运算的结果正是密文920ECF10，即我们要找的密文大概率就是sgfnyd。

        再比如，我们要破解的密文为281DAF40，第一次R运算后的结果并未在末节点中找到，则再重复执行一次H运算+R运算，这时我们又得到了kiebgt，则我们再从起点aaaaaa开始计算，这次得到我们要找的密文为aaaaaa。

        当然，如果是重复了k=2次之后，仍然没有在末节点中找到对应的值，则可以断定，所需的明文不在这张集合中——集合并未存储长度大于k的哈希链，因此再计算也没有意义。

        从上面的两个破解示例可以归纳出基于散列链集的破解步骤（假定散列链的长度为k）：

步骤1：假设我们要破解的密文将会出现在由每条链的第k个H函数作用之后的密文组成的集合之中；

子步骤1.1：对密文执行一次R运算；

子步骤1.2：在散列集中寻找能匹配末节点的（明文，密文）对儿，如果能找到，则从起始点开始计算，直到找到能匹配的明文并成功退出；如果找不到，则执行步骤2；

步骤2：假设我们要破解的密文将会出现在由每条链的第k-1个H函数作用之后的密文组成的集合之中；

子步骤2.1：对密文执行一次R运算+一次H运算+一次R运算；

子步骤2.2：在散列集中寻找能匹配末节点的（明文，密文）对儿，如果能找到，则从起始点开始计算，直到找到能匹配的明文并成功退出；如果找不到，则执行步骤3；

步骤3：仿照步骤2，依次假设密文将出现在第k-i个H函数作用之后的密文组成的集合之中，并对密文执行一次R运算再加上（i-1）的（H运算+R运算），直到找到能匹配的明文并成功退出或直到i=k。

        至此，由上述分析可知，尽管增大k值，可以提高空间利用率，但却增加了破解密文时的计算量。相信到这里大家可以理解开头所说的“彩虹表并不是简单地“以空间换时间”，而是一种双向交易，在二者之间达到平衡”这句话的含义。即增大k值，本质上就是以时间换空间，减小k值，就是以空间换时间。RainbowCrack中rtgen工具使用的默认k值好像是2100。

约简函数R存在的问题

        在构造哈希链的时候，一个优秀的函数R功不可没。首先R函数需要能将值域限定在固定的范围——给定的长度范围、给定的字符取值范围等之内，否则的话，哈希链中大量的计算结果并不在可接受的范围内，一条链无法对应多个明文，链条就失去了意义；其次R必须同哈希函数一样，尽量保证输出值在值域中的均匀分布，以减少碰撞的概率。

        但实际上，很难找到能满足以上条件的完美的R函数。当计算中发生碰撞时，就会出现如下情况（详见参考博文7）：

        图中加粗的部分，对应的明文和对应的密文是完全重复的，因此这两条哈希链能解密的明文数量就远小于理论上的明文数量2k。而不幸的是，由于集合只保存了链条的首末节点，因此这样的重复链条并不能被迅速地发现。随着碰撞的增加，这样的重复链条会逐渐造成严重的冗余和浪费。

闪亮登场的彩虹表

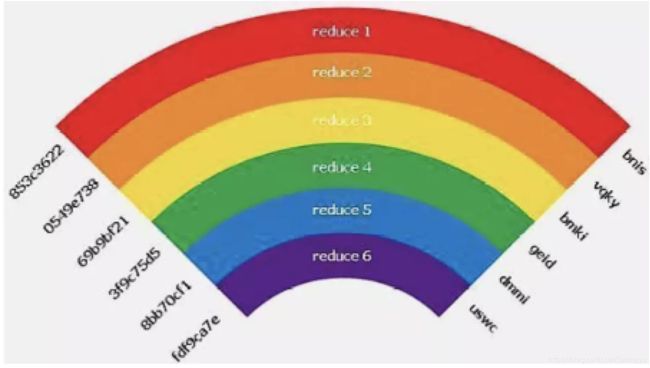
        为了解决R函数存在的问题，2003年Philippe Oechslin在其论文中提出在各步的运算中，并不使用同一个R函数，而是分别使用R1...Rk共k个不同的函数。这样一来，即使偶然发生碰撞，通常会是如下情形：

        容易看到，当两个链条发生碰撞的序列位置不同时，由于后续的R函数不一样，使得链条的后续部分也不相同，从而极大地减少了链条中的重复链路，保证了链条的有效性。同时，即便在极端情况下，有两个链条在同一个序列位置上发生碰撞，导致后续链条完全一致，这样的链条也会因为末节点相同而被检测出来，可以丢弃其中一条而避免浪费存储空间。如果把每条这样的哈希链，用不同的颜色标识，这就产生了彩虹表（这也就是彩虹表名称的由来）。

 

        彩虹表的破解步骤同散列链集十分相似，唯一不同的是计算过程中需要使用不同的约简函数，因而不再赘述其破解过程。

彩虹表中的约简函数R集

        前面介绍了约简函数所需要具备的两条性质：

1.R需要能将值域限定在固定的范围之内。实际上，在计算和下载彩虹表时，不同类型的明文（明文长度和字符集的差异）和使用的散列算法H（MD5、SHA等），其需要的彩虹表是不同的。例如彩虹表下载网站（参考博客3）就按照不同的哈希函数、字符集和密码长度等的不同分成了很多不同的库，这些库使用的R函数都是不一样的，只有这样才能保证R函数的值域和所需猜解的明文取值范围保持一致。

2.R需要尽量保证输出值在值域中均匀分布，以减少碰撞的概率。对于这条性质，一般是利用H函数生成的哈希值本身的均匀性来实现的。

彩虹表的防御

        由彩虹表破解原理可知，彩虹表的防御可以在两个方面做文章：一个是明文本身，一个是散列函数H。

        首先介绍对于散列函数H，我们能做的事情和不能做的事情。比如我们可以将H定义为一千次MD5后的结果。由于H在算法中的重复性，当单次运算的H函数耗时增加，意味着彩虹表的生成时间也会大大的增加，从而导致破解成本的增加。除此之外，参考博客9中强烈反对人们将不同的hash函数组合在一起用的方案甚至使用自定义的hash函数。因为这种方式不仅带来的效果很微小，反而可能带来一些互通性的问题，甚至有时候会让hash更加不安全。博客中建议使用标准的经过严格测试的hash算法，并通过采用一个安全变量或者迭代次数作为参数的方式，让hash过程变得足够的慢（甚至故意选择一些大量消耗CPU资源的hash函数），从而使彩虹表的生成时间变得极长。当然这样也会使得我们自身的系统在接收用户认证请求时的性能受到影响，因而需要综合考量。

        我们再来说说对明文本身我们能做什么。对明文最常用的方法就是加盐（salt），加盐是指我们不直接对明文本身做哈希运算，而是在明文的后面添加随机生成的字符串，然后对添加后的字符串做哈希运算（比如保存用户的账号密码时，我们对用户的明文密码加随机字符串，然后再做哈希运算，最终存储的是哈希运算后的值）。对于为什么加盐能有效地防止彩虹表的攻击，绝大多数的博客都会说这是由于彩虹表在生成的过程中，针对的是特定的函数H，H如果发生了改变，则已有的彩虹表数据就完全无法使用。如果每个用户都用一个不同的盐值，那么每个用户的H函数都不同，则必须要为每个用户都生成一个不同的彩虹表，这就大大提高了破解难度（参考博客6、7、8等）。对此我不以为然。

        为什么说加盐之后，每个用户的H函数就不同了呢？H函数不还是那个H函数么？发生变化的是明明是明文本身啊！考虑一种极端情况，假设一个用户设置的明文密码本身就是使用哈希算法得到的随机码，我们给它再添加一个随机码，并进行哈希运算，得到的密文不还是可以通过彩虹表破解么？加盐的意义到底何在呢？参考博客1中说由于用户一般很少会使用：!@#$%^*=+之类的特殊符号，而这些符号可以通过加盐实现。加盐相当于增加了明文的值域，因而在造表的过程中设计R函数就需要考虑到映射回这些特殊符号，这就增大了造表的空间和难度。对于这个说法，一开始我觉得有一定道理，但直到我看到参考博客4。该博客中说到，ascii-32-95这个字符集涵盖了键盘上所有的95个字符，即：!"#$%&'()*+,-./0123456789:;<=>?@ABCDEFGHIJKLMNOPQRSTUVWXYZ[\]^_`abcdefghijklmnopqrstuvwxyz{|}~。也就是说，如果加盐的作用只是增加特殊符号的话，那么意义不大，因为这无非就是让破解者多了一次选择彩虹表的时间（前面已经提到过，参考博客3按照不同的哈希函数、字符集和密码长度等的不同分成了很多不同的库）。

        让我们换一个角度来思考这个问题：假设有Tom和Jerry两个用户来注册同一个网站，两个用户的用户名分别就是Tom和Jerry。尽管两人都不知道对方的密码，但我们假设：恰巧，恰巧这两个用户都使用“TomAndJerry”这一个字符串作为各自的密码。此时，尽管这两个用户使用的是同一个明文密码，但由于这两个用户并非同一个用户，因而我们的网站系统会给这两个用户的明文密码加上不同的随机字符串。比如加上随机字符串后的两个明文密码为：TomAndJerry134F5G5HIJ*和TomAndJerryPO3E68H&T86，然后我们分别对这两个字符串再执行哈希运算，最终得到了两个完全不同的密文。要知道，破解者实际上期望最终破解得到的是TomAndJerry，而不是加了不同随机字符串之后的明文。从这个角度来看，我们对同一个明文字符串添加不同的随机字符串，然后再进行哈希运算，最终得到两个不同的密文，这个操作过程是不是等价于我们对同一个明文使用不同的哈希算法进行运算，并最终得到两个不同的密文呢？所以从这个角度来说，参考博客6、7、8中的那种说法也有一定的道理。这里再总结一下：如果每个用户都用一个不同的盐值，必须要为每个用户都生成一个不同的彩虹表，这就大大提高了破解难度。从这句话可以看出，加盐可以让攻击者无法使用查表和彩虹表的方式对大量hash进行破解。但是依然无法避免对单个hash的字典和暴力攻击。高端的显卡(GPUs)和一些定制的硬件每秒可以计算数十亿的hash，所以针对单个hash的攻击依然有效。为了避免字典和暴力攻击，我们可以采用一种称为key扩展(key stretching)的技术（以下来自参考博客9）。

        思路就是让hash的过程便得非常缓慢，即使使用高速GPU和特定的硬件，字典和暴力破解的速度也慢到没有实用价值。通过减慢hash的过程来防御攻击，但是hash速度依然可以保证用户使用的时候没有明显的延迟。

        key扩展的实现是使用一种大量消耗cpu资源的hash函数。不要去使用自己创造的迭代hash函数，那是不够的。要使用标准算法的hash函数，比如PBKDF2或者bcrypt。PHP实现可以在这里找到。

        这些算法采用了一个安全变量或者迭代次数作为参数。这个值决定了hash的过程具体有多慢。对于桌面软件和手机APP，确定这个参数的最好方式是在设备上运行一个标准测试程序得到hash时间大概在半秒左右的值。这样就可以避免暴力攻击，也不会影响用户体验。

         如果是在web应用中使用key扩展hash函数，需要考虑可能有大量的计算资源用来处理用户认证请求。攻击者可能通过这种方式来进行拒绝服务攻击。不过我依然推荐使用key扩展hash函数，只是迭代次数设置的小一点。这个次数需要根据自己服务器的计算能力和预计每秒需要处理的认证请求次数来设置。对于拒绝服务攻击可以通过让用户登陆的时候输入验证码的方式来防御。系统设计的时候一定要考虑到这个迭代次数将来可以方便的增加或降低。

        如果你担心计算机的能力不够强，而又希望在自己的web应用中使用key扩展hash函数，可以考虑在用户的浏览器运行hash函数。Stanford JavaScript Crypto Library包含了PBKDF2算法。

        

参考博客：

1、http://www.360doc.com/content/17/0706/16/37475013_669359523.shtml 彩虹表破解开机密码、MD5算法等原理

2、https://lasecwww.epfl.ch/pub/lasec/doc/Oech03.pdf  Making a Faster Cryptanalytic Time-Memory Trade-Off（论文）

3、http://project-rainbowcrack.com/table.htm  List of Rainbow Tables

4、http://project-rainbowcrack.com/charset.txt 彩虹表的字符集表

5、https://blog.csdn.net/Saintyyu/article/details/102641627 为什么说MD5是不可逆哈希算

6、https://www.jianshu.com/p/131eddd18f6b 关于彩虹表的介绍

7、https://www.zhihu.com/question/19790488?sort=created 什么是彩虹表

8、https://www.jianshu.com/p/732d9d960411 彩虹表

9、https://wooyun.js.org/drops/%E5%8A%A0%E7%9B%90hash%E4%BF%9D%E5%AD%98%E5%AF%86%E7%A0%81%E7%9A%84%E6%AD%A3%E7%A1%AE%E6%96%B9%E5%BC%8F.html  加盐保存密码以防止彩虹表的正确方式