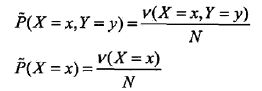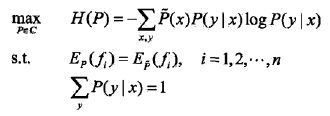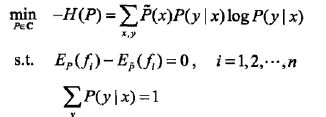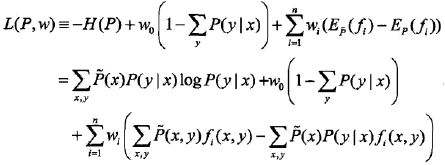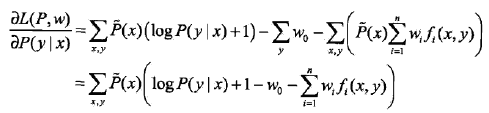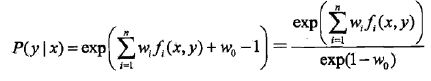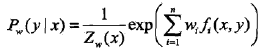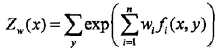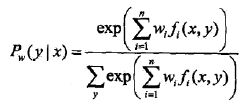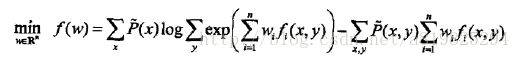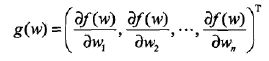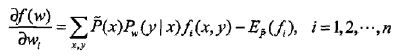【机器学习】最大熵算法 整理
最大熵模型由最大熵原理推导实现
1.最大熵原理
最大熵原理认为,学习概率模型时,在所有可能的概率模型(分布)中,熵最大的模型是最好的模型。通常用约束条件来确定概率模型的集合,所以,最大熵原理也可以表述为在满足约束条件的模型集合中选取熵最大的模型。
熵满足下列不等式: ![]() 式中,|X|是X的取值个数,当且仅当X的分布是均匀分布时右边的等号成立。
式中,|X|是X的取值个数,当且仅当X的分布是均匀分布时右边的等号成立。
即当X服从均匀分布时,熵最大。
下面通过一个例子来介绍一下最大熵原理:
问题:假设随机变量X有5个取值{A,B,C,D,E},要估计取各个值的概率P(A),P(B),P(C),P(D),P(E)。
解:这些概率值满足以下约束条件:P(A)+P(B)+P(C)+P(D)+P(E) = 1
满足这个约束条件的概率分布有无穷多个。如果没有任务其他信息,仍要对概率分布进行估计,一个办法就是认为这个分布中各个值是相等的:P(A) = P(B) = P(C) = P(D) = P(E) = 1/5
有时,能从一些先验知识中得到一些对概率值的约束条件,例如:P(A) + P(B) = 3/10
满足上面两个约束条件的概率分布仍然有无穷多个。在缺少其他信息的情况下,可认为A和B是等概率的,C,D与E是等概率的,于是:P(A) = P(B) = 3/20 及 P(C) = P(D) = P(E) = 7/30
2.最大熵模型的定义
最大熵原理是统计学习的一般原理,将它应用到分类得到最大熵模型。
学习的目标是用最大熵原理选择最好的分类模型
(2)给定训练数据集,可以确定联合分布P(X,Y)的经验分布和边缘分布P(X)的经验分布。
其中,v(X=x,Y=y)表示训练数据中样本(x,y)出现的频次,v(X=x)表示训练数据中输入x出现的频数,N表示训练样本容量。
(3)用特征函数f(x,y)描述输入x和输出y之间的某一个事实。其定义是
特征函数f(x,y)关于模型P(Y|X)与经验分布![]() 的期望值:
的期望值:![]()
如果有n个特征函数,那么就有n个约束条件。
定义最大熵模型
则模型集合C中条件熵H(P)最大的模型称为最大熵模型。式中的对数为自然对数。
3.最大熵模型的学习
最大熵模型的学习过程就是求解最大熵模型的过程。最大熵模型的学习可以形式化为约束最优化问题。
对于给定的训练数据集![]() 以及特征函数
以及特征函数![]() ,
,
最大熵模型的学习等价于约束最优化问题:
按照最优化问题的习惯,将求最大值问题改写成等价的求最小值问题:
将约束最优化的原始问题转换为无约束最优化的对偶问题,通过求解对偶问题求解原始问题
(1)首先,引进拉格朗日乘子,定义拉格朗日函数L(P,w):
对偶问题是:![]()
由于拉格朗日函数L(P,w)是P的凸函数,原始问题的解与对偶问题的解释等价的。
(2)然后求解对偶问题内部的极小化问题![]() L(P,w)。
L(P,w)。![]() L(P,w)是w的函数,
L(P,w)是w的函数,
求偏导数:
令偏导数等于0,在![]() >0的情况下,解得:
>0的情况下,解得:
此时,就可以利用梯度下降、拟牛顿等最优化方法进行学习了,类似于逻辑斯蒂回归求解参数w。
4.极大似然估计
证明对偶函数的极大化等价于最大熵模型的极大似然估计
(1)已知训练数据的经验概率分布![]() ,条件概率分布P(Y|X)的对数似然函数表示为:
,条件概率分布P(Y|X)的对数似然函数表示为:
当条件概率分布P(y|x)是最大熵模型时,对数似然函数为
(2)对偶函数
5.模型学习的最优化算法
最大熵模型学习归结为以似然函数为目标函数的最优化问题,通常通过迭代算法求解。从最优化的观点看,这时的目标函数具有很好的性质。它是光滑的凸函数,因此多种优化方法都适用,保证能找到全局最优解。
下面以拟牛顿法为例,对于最大熵模型而言
相应的拟牛顿法BFGS算法如下
参考文献 :《统计学习方法》
附:我经历过的关于 一道面试题:
有8个硬币,如果知道有一个异常硬币(比正常硬币重或轻),给你一个称,称几次可以得出异常硬币?
答案:3次。
第一次、两边分别称4个硬币,取出 重或轻的 四个硬币。
第二次、两边分别称2个硬币,取出 重或轻的 两个硬币。
第三次、两边分贝称1个硬币,得出 重或轻的 一个硬币。
那如果不知道异常硬币的特征呢?答案也是称 3 次。
第一次、两边分别放两个,如果相等,则异常硬币再另四个中;如果不相等,则异常硬币再这个四个中。
第二次、从正常硬币中取两个,再从异常硬币中取出两个。如果相等,则另外两个中有一个是异常硬币;如果不相等,则这个两个硬币中,存在异常硬币。
第三次、从正常硬币中取一个,再从异常硬币中取一个。如果相等,则另一个是异常硬币;如果不相等,则这个是异常硬币。