【计算机图形】Perlin Noise 实例和理解
Perlin noise
一、 背景介绍
分形：
分形，具有以非整数维形式充填空间的形态特征。通常被定义为“一个粗糙或零碎的几何形状，可以分成数个部分，且每一部分都（至少近似地）是整体缩小后的形状”，即具有自相似的性质。分形（Fractal）一词，是芒德勃罗创造出来的，其原意具有不规则、支离破碎等意义。1973年，芒德勃罗（B.B.Mandelbrot）在法兰西学院讲课时，首次提出了分维和分形的设想。（百度百科）
分形在自然界中随处可见：
生成方式：
Perlin noise 就是一种非常有用强大的算法，常用于生成看似杂乱而又有序的内容。尤其特别适合用于游戏和其他视觉媒体，如电影。它的创始人Perlin也因为最先运用此技术而获得奥斯卡奖。
| 噪音维数 | 原始噪音 (Grayscale) | 实例 |
|---|---|---|
| 1维 |  |
 Using noise as an offset to create handwritten lines. |
| 2维 |  |
 By applying a simple gradient, a procedural fire texture can be created. |
| 3维 |  |
 Perhaps the quintessential use of Perlin noise today, terrain can be created with caves and caverns using a modified Perlin Noise implementation. |
二、原理
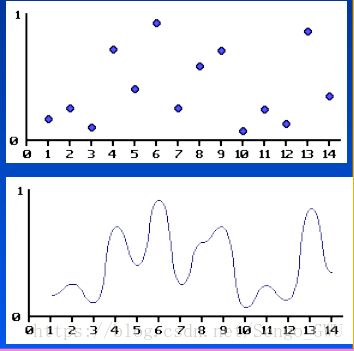
对一维，如上图，先分配随机的散点，再对这些点进行插值获得连续的曲线。此处需要注意的是需要控制波长，否则可能导致Aliasing(不知道中文应该如何翻译这个词，因为其并不代表锯齿)。
此处细节Prof. James给我的邮件答复内容：
Because the wavelength is about the size ofthe lattice. Therefore the frequency is also narrowly limited. You are going to add a number of thesesignals to get the 1/f noise. You need to know the frequency you are about toadd in order to be able to sample at the Nyquist limit.
对二维
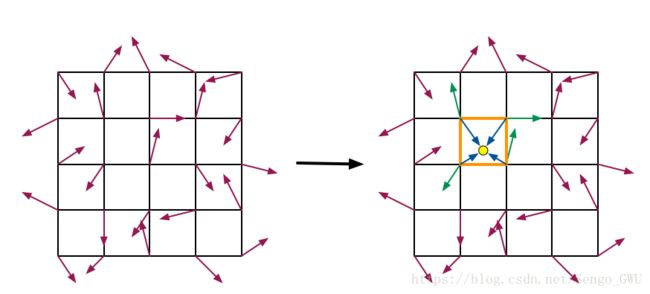
- 定义一个晶格结构，每个晶格的顶点有一个“伪随机”的梯度向量。对于二维的Perlin噪声来说，晶格结构就是一个平面网格，三维的就是一个立方体网格。
- 输入一个点（二维的话就是二维坐标，三维就是三维坐标，n维的就是n个坐标），我们找到和它相邻的那些晶格顶点（二维下有4个，三维下有8个，n维下有2n2n个），计算该点到各个晶格顶点的距离向量，再分别与顶点上的梯度向量做点乘，得到2n2n个点乘结果。
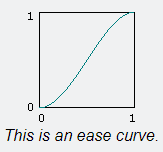
- 使用缓和曲线（ease curves）来计算它们的权重和。在原始的Perlin噪声实现中，缓和曲线是s(t)=3t2−2t3s(t)=3t2−2t3，在2002年的论文6中，Perlin改进为s(t)=6t5−15t4+10t3s(t)=6t5−15t4+10t3。由高等数学可以知道，函数越是高阶可导函数曲线越是平滑，s(t)=3t2−2t3s(t)=3t2−2t3在一阶导满足连续性，但它的二阶导在晶格顶点处（即t = 0或t = 1）不为0，会造成明显的不连续性。s(t)=6t5−15t4+10t3s(t)=6t5−15t4+10t3在二阶导上仍然满足连续性。
如上图，每个晶体格的顶点都有一个递度向量，梯度向量代表该顶点相对单元正方形内某点的影响是正向还是反向的。这些梯度向量并不是完全随机的，而是由单位正方体（3维）的中心点指向各条边中点的12个向量： (1,1,0),(-1,1,0),(1,-1,0),(-1,-1,0), (1,0,1),(-1,0,1),(1,0,-1),(-1,0,-1), (0,1,1),(0,-1,1),(0,1,-1),(0,-1,-1) 采用这些特殊梯度向量的原因在Ken Perlin’s SIGGRAPH 2002 paper: Improving Noise这篇文章里有具体说明。主要是为了避免“镜像”现象。伪随机指的是每次生成的一串随机数如（1,3,7,2），下一次生成的随机数依然是一样的（1,3,7,2）。
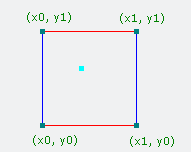
如下图，此处蓝点代表2D平面输入的（x,y）坐标点和其周围的4个晶体格顶点。
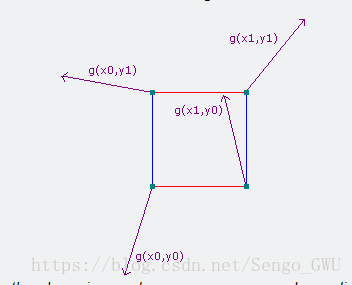
对每个顶点，我们生成一个伪随机的递度向量。其中，指向中心点的递度向量定义为正方向，反之则为负反向。如下图。
其中，这些伪随机递度向量在此图中并不是精确的，只是用于示意。Perlin给出了在3维中这些递度向量的值。
(1,1,0),(-1,1,0),(1,-1,0),(-1,-1,0),
(1,0,1),(-1,0,1),(1,0,-1),(-1,0,-1),
(0,1,1),(0,-1,1),(0,1,-1),(0,-1,-1)选取这些值的原因在Perlin 2002年的论文中解释：Ken Perlin's SIGGRAPH 2002 paper: Improving Noise.
接下来，我们对这2个向量（距离向量和递度向量）进行点成。对3D：
grad.x * dist.x + grad.y * dist.y + grad.z * dist.z这么做能实现是因为对2个向量的点成，等于COS它们之间的夹角再乘以它们的模长。
dot(vec1,vec2) = cos(angle(vec1,vec2)) * vec1.length * vec2.length因此，如果2个向量有相同的方向，相当于：
1 * vec1.length * vec2.length方向相反则：
-1 * vec1.length * vec2.length垂直则为0. 因此，它们的点积，如果为正则表示距离向量和递度向量方向相同，反之则为负。如图，黄色区域表示结果为正，蓝色区域表示结果为负。
如果我们给定的递度向量是周期性的值，即内部的值是周期重复的如（134134），则噪音本身也会无缝的衔接在一起。因此我们的代码中需要对递度的值进行重复。
对于这4个距离向量和递度向量点成后的结果（3D则8个）进行插值计算（可以使用sin或者cos），从而获得一种连续的加权平值。并且，我们希望插值结果尽量光滑，因此引入了eaze curve 缓和曲线:
对于0-1的映射，我们都是用u,v来表示其横纵坐标轴。eaze function的定义为：
6t5-15t4+10t3也就是说对于一个晶体格，我们通过对4个点进行插值可以获得整个晶体格范围内所有的点。
三、代码
我们需要2步来使Perlin 噪音无缝衔接。第一步，我们要使noise function本身是周期的。因此，我们将perm重复了一次，则其noise计算后的值也是重复的。
import random
import math
from PIL import Image
perm = range(256) # 随机排列
random.shuffle(perm)
perm += perm # 使其有周期
dirs = [(math.cos(a * 2.0 * math.pi / 256), # X方向cos，Y方向sin 插值
math.sin(a * 2.0 * math.pi / 256))
for a in range(256)]
def noise(x, y, per):
# Perlin noise is generated from a summation of little "surflets" which are the product of a randomly oriented
# gradient and a separable polynomial falloff function.
def surflet(gridX, gridY): # gridX, gridY 为晶体格顶点的坐标
distX, distY = abs(x-gridX), abs(y-gridY) # 距离向量
polyX = 1 - 6*distX**5 + 15*distX**4 - 10*distX**3 # polynomial falloff function
polyY = 1 - 6*distY**5 + 15*distY**4 - 10*distY**3
# 此处hash函数用于每个输入坐标都有一个对应的排列值
hashed = perm[perm[int(gridX) % per] + int(gridY) % per]
grad = (x-gridX)*dirs[hashed][0] + (y-gridY)*dirs[hashed][1]
return polyX * polyY * grad
intX, intY = int(x), int(y)
# 4个方向结果的累加，图中黄色和蓝色面积的累加。4个晶体格。
return (surflet(intX+0, intY+0) + surflet(intX+1, intY+0) +
surflet(intX+0, intY+1) + surflet(intX+1, intY+1))第二步，讲周期和频率联系起来：
def fBm(x, y, per, octs):
val = 0
for o in range(octs):
val += 0.5**o * noise(x*2**o, y*2**o, per*2**o)
return val
size, freq, octs, data = 128, 1/32.0, 5, []
for y in range(size):
for x in range(size):
data.append(fBm(x*freq, y*freq, int(size*freq), octs))
im = Image.new("L", (size, size))
im.putdata(data, 128, 128) # 此处128不是图片size
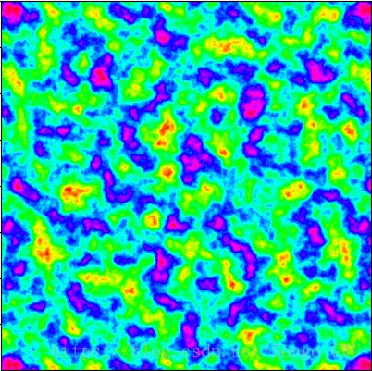
im.save("noise.png")结果图：
通过colormap将灰度图映射到对应颜色：
参考文献：
1. How do you generate tileable Perlin noise?
2. Understanding Perlin Noise
3.【图形学】谈谈噪声