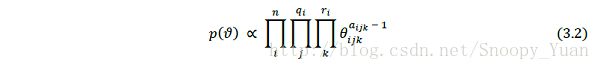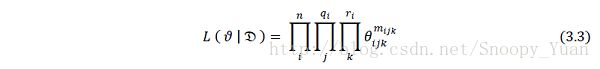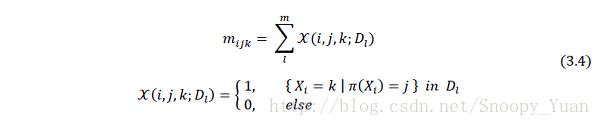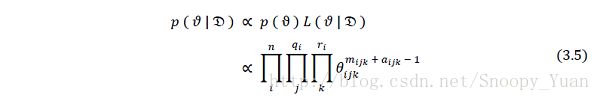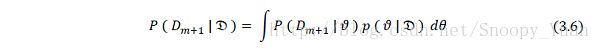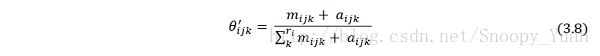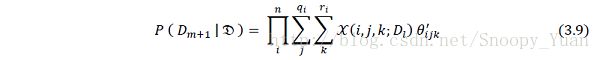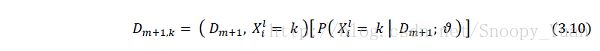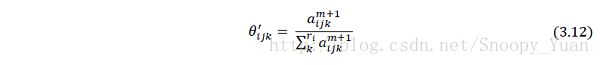概率图模型基础 - 贝叶斯网络参数学习（贝叶斯估计+碎权更新法）

前序

贝叶斯网络是一种性能优秀的不确定推理方法。其模型结构解释性好，推理过程本质与人的思维模式相似。

要采用贝叶斯网络进行推理分析，首先考虑网络模型的搭建。与神经网络的黑盒模式相反，贝叶斯网络模型要真实的反应研究对象，于是需要知道其网络结构和参数。现在已经有越来越多的研究关注于如何通过数据进行贝叶斯网络结构和参数的学习，但实际中我们往往面临数据集的局限，这是专家知识对建模来说依然十分重要。

本文考虑整合专家知识，在数据驱动的大思路下进行贝叶斯网络的参数学习。通过分析贝叶斯估计的实现过程来给出完整数据样本下的参数学习方法，同时考虑碎权更新法来解决数据缺失的挑战。

（注：本文主要是笔者在项目背景下进行基础学习的总结笔记。错误难免，还望得到广大网友们的热心指导。）

贝叶斯网建模思路

现在的一种主流思路是将网络学习的内容加入贝叶斯网推理模型之中，以期实现模型动态优化，提升实时精度。

当数据量可能会面临限制时，可考虑先依赖专家知识进行初始化建模，然后利用在线流数据分析的方式增量的迭代优化模型。根据难以程度，可采取下图所示三步走计划：

下面重点对参数学习更新部分进行叙述。

贝叶斯网参数学习

贝叶斯网的学习是指通过数据分析，获取贝叶斯网的过程，它包括参数学习与结构学习两个部分。参数学习是指已知网络结构，确定网络参数的问题。而我们这里对参数学习的角色定位是：在已知初始化模型的基础上（包括初始化结构和初始化参数），基于实时获取的新数据，通过参数学习来优化更新模型。所以这里的参数学习用于参数的实时更新。为整合先验知识，采用“贝叶斯估计”来实现参数学习的基本方法，同时采用碎权更新法来实现数据样本不完整场景下的实时近似估计。

1.基础知识

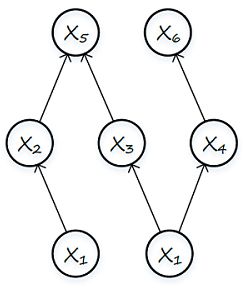
一个贝叶斯网包含有根节点、叶节点、中间节点三类节点。下图为一个贝叶斯网示例：

上图中：X1，X2 为根节点，X2，X3，X4 即为中间节点，X5，X6 为叶节点。各节点间关系由有向边标识，如 X2 为 X1 的子节点，X5 的父节点有 X2 和 X3 。每个节点对应变量，记为：X = { X1, X2, …, Xn }，其中 n 为变量个数，如图3-2中 n = 6。

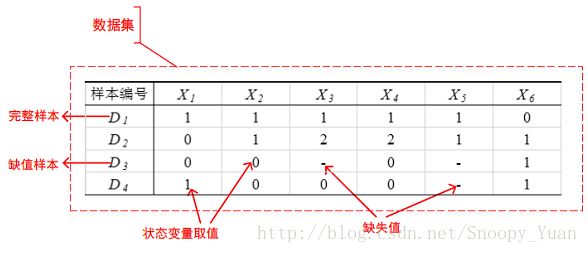
由 X 的所有或部分变量状态构成的向量称为数据样本，多个样本构成数据集（简称数据）。如下图表示了下图3-2的一个数据集样例：

我们记一个贝叶斯网为：N = { Y, ϑ }，其中 Y 表示贝叶斯网模型（DAG）， ϑ 表示贝叶斯网模型参数（CPT）。那么，考虑节点 Xi（i ~ 1 ,…, n），其父节点 π(Xi) 的取值组合为 j（j ~ 1 ,…, qi），节点状态取值为 k（k ~ 1 ,…, ri）。那么网络的参数 ϑ 记如下式：

所以一个贝叶斯网共有 个参数，由于某个节点状态概率和恒为1，故需要我们学习的独立参数数目是 。

2.贝叶斯估计整合先验知识

对于一个贝叶斯网 N = { Y, ϑ } ，在完整数据 D = ( D1, D2, …, Dm ) 下采用贝叶斯估计对其进行参数估计的流程可分为下面几步：

2.1.专家知识转化为先验概率分布

为方便先验参数 p(ϑ) 的确定，一般假设 p(ϑ) 具有全局独立性，p(ϑi) 具有局部独立性，p(ϑij) 是狄利克雷分布 D [ aij1, aij2, …, aijri ] 。据此，先验分布 p(ϑ) 规范为乘积狄利克雷分布，如下式：

于是，只需依靠专家知识给出狄利克雷分布的超参数 {aijk} 即可。

2.2.基于数据得到后验概率分布

设数据 D = ( D1, D2, … , Dm ) 满足独立同分布性质，则参数 ϑ 在数据 D 下的似然函数可写为：

上式中，mijk 是表示数据包含当前状态 (i,j,k) 的特征量，其定义如下：

于是由贝叶斯公式计算出后验概率如下：

所以，后验概率也是乘积狄利克雷分布。

2.3.计算下一个样本的概率分布（条件概率）

某个节点的条件概率表包含了父节点状态组合下该节点处于各状态的概率，实际上就是样本取值的概率分布。考虑下一个样本 Dm+1 = ( X1, X2, …, Xn ) ，根据网络后验概率计算得到其概率分布如下式：

根据全局独立性和马尔可夫性等性质，上式可化简为：

上式所代表的概率分布可以映射到一个与当前网络结构相同的贝叶斯网 N = { Y, ϑ’ }，其参数 ϑ’ = { θ’ijk } 是静态的，其分布 p(θij.) 满足狄利克雷分布，超参数为 [ mijk + aijk ] ，ϑ’ 计算式如下：

于是得出 Dm+1 的概率分布最终计算式如下：

3.数据残缺下的贝叶斯估计

在数据出现缺失值的情况下，为了尽可能地实现数据的最大化利用，采用碎权更新法，其核心思想是：将缺值的样本按照可能取值进行修补，对每个修补样本按照其可能性赋给权重，这样的样本称之为碎权样本，然后基于碎权样本进行贝叶斯估计。该方法的核心是碎权样本权重计算。

设基于之前的专家知识及数据得到的关于贝叶斯网的后验概率分布为 p(ϑ│D) ，对应狄利克雷分布的超参数为 [aijk^m] 。现在有缺值数据样本 Dm+1 ，{Xi^l} 是其中缺值变量的集合，则 Xi^l 取某值 k 的概率是 P( Xi^l = k │ Dm+1; ϑ )，以此为权重，可得到新的碎权数据样本如下：

于是，基于新的碎权样本进行参数更新，根据之前讨论，可直接加权更新狄利克雷分布超参数：

于是此时贝叶斯网的参数是：

代回式(3.9)即可算出新的条件概率表。

4.完整算法

综上，给出数据不完整条件下的贝叶斯估计参数学习算法如下：

算法1：基于碎权更新的贝叶斯估计算法

输入： 贝叶斯网的结构 Y ，实时数据 D ；
输出： 贝叶斯网参数估计 ϑ ； 
流程：
1.  expert knowledge to initial hyper-parameters aijk in Dirichlet distribution of prior p(ϑ) ;
2.  while (D) :
        for  Dm  in  D :
            for  i,  j,  k :
                if  Dm  is  incomplete  for  Xi:     
                        get θijk^' using (3.12);
                else    get θijk^' using (3.8) ;
            update ϑ using (3.1) ;
            update P ( Dm+1 │ ϑ ) using (3.9)  ;
3.  output ϑ as well as P ( D_more  │ ϑ ) ;

思考与展望

上面给出一套贝叶斯网络的基本参数学习方法，包括先验知识的整合和缺值样本问题的解决。进一步研究可着眼于以下一些问题：

• 网络复杂时先验参数（狄利克雷分布超参数）数目太多，专家给定工作量大，有没有什么方法可以减小专家给定时的工作量？（引入AND-OR将概率逻辑化？）

• 迭代学习过程要对每个变量（即网络节点）进行更新计算，计算量随系统规模扩大而急剧扩大。有没有什么方法优化计算减小计算量？（比如团树传播算法（CTP）的融入以实现共享计算？）

还望大家多多提出相关问题和建议。