机器学习基础:集成学习方法应用实验(RF、GBDT)
集成学习正广泛地被应用于机器学习/数据挖掘的实际项目之中。掌握集成学习方法,了解其特性与适用场景,对机器学习理论与实践的结合帮助甚大。这里,我们考察集成学习最重要的两种类型:装袋(Bagging)与提升(Boosting),从其两大算法入手:Random Forest、GBDT,基于自己生成的数据集场景和UCI数据集开展实验,对比分析算法的表现。
基础简要回顾
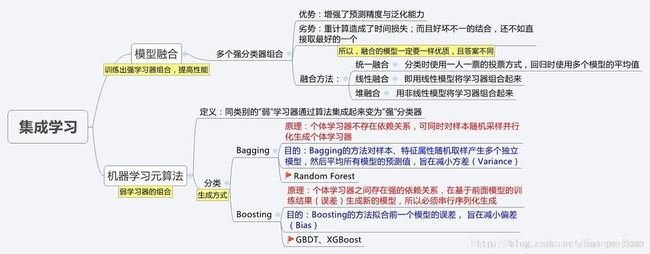
关于集成学习,引用博文笔记︱集成学习Ensemble Learning的描述如下图:
从图中可以看出,集成学习包括元算法和模型融合两方面,元算法提供了从个体弱学习器到集成强学习器的实现,模型融合则在强学习器的基础上,设计结合策略进一步提升性能,元算法按照个体弱学习器之间的依赖关联关系,又分为Boosting类算法和Bagging类算法。下面对其中最基础的几大算法进行概述。
Bagging
Bagging(装袋法)基于自助采样法(bootstrap sampling)来生成训练数据,通过多轮有放回的对初始训练集进行随机采样,多个训练集被并行化生成,对应可训练出多个基学习器,再将这些基学习器结合,构建出强学习器。
因为是随机有放回的采样(自助法),初始训练集中的样本既有可能多次出现在某个采样集中,又有可能不出现,通过统计计算,初始集约有63.2%的样本出现在训练集当中,剩下的36.8%样本可用于模型泛化能力的验证,这种方法称为“包外估计”(out-of-bag-estimation),同时包外样本还可以用于决策树的剪枝、神经网络早停控制等等。
装袋法的本质是引入了样本扰动,通过增加样本随机性,达到降低方差的效果,这种方法在决策树、神经网络等易受样本扰动影响的模型上效果尤为明显。
RF
RF-Random Forest(随机森林)是Bagging的扩展,主要面向决策树模型,在Bagging法构造决策树基学习器的基础上,对每步划分时的当前特征集进行随机选择以生成随机特征子集,然后再在子集中选择最优特征进行划分,进而训练出当前的基学习器。
在进行当前节点特征(假设 d 个)随机选择时,子集特征数目 k 推荐取值 k≈log2(d) 。较小的特征子集加速了训练,减小了计算开销。
随机森林通过特征子集的随机选择的方式,引入了特征扰动,在装袋法的基础上,这种方法可进一步降低了方差,增强了模型的泛化精度。
AdaBoost
不同与Bagging,Boosting算法是一种串行序列化方法,它的前后两个基学习器间强关联,后面学习器的训练往往建立在前面学习器的训练结果基础上。
AdaBoost算法是Boosting算法族的典型代表,它基于“残差逼近”的思路,采用“重赋权法”,即是根据每个基学习器的结果调整样本权重,生成新的更加关注于错误样本的数据分布,然后在新数据分布上继续以损失函数最小为目标训练新的基学习器。同时根据这些基学习器的训练误差,对基学习器赋权,最后采用加权求和得出集成模型。
AdaBoost旨在减小学习的偏差,能够基于泛化精度很差的学习器个体构建出强集成。
GBDT
GB(Gradient Boosting)可以被看作是AdaBoost的变体,最大不同之处在于GB在迭代优化过程中采用了梯度计算而非加权计算。GB通过在每一步残差减少的梯度方向上训练新的基学习器,最后通过集成得到强学习器。
GBDT算法(Gradient Boosting Decision Tree)是一种基于GB框架下的决策树集成学习算法。基学习器采用的是以最小化平方误差为目标的回归树,迭代的过程建立在对“之前残差的负梯度表示”的回归拟合上,最后累加得到整个提升树。
同其他Boosting算法一样,GBDT也关注于降低拟合的偏差。
分类实验
这里我们采用2个sklearn.datasets自带的UCI数据集进行实验。两种算法(RF和GBDT)的实现基于sklearn.ensemble。这里查看完整实验代码-GitHub。
数据集
2个数据集的简要信息如下:
| # | 总类别数 | 特征数 | 样本数 | 其他 |
|---|---|---|---|---|
| IRIS-鸢尾花数据集 | 3 | 4 | 150(每类50条样本) | 特征均为数值连续型、无缺失值 |
| Breast_Cancer-乳腺癌数据集 | 2 | 30 | 569(正样本212条,负样本357条) | 特征均为数值连续型、无缺失值 |
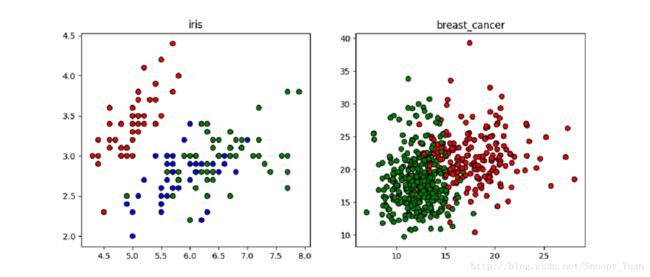
加载数据,通过matplotlib绘制出散点图示意如下:
模型训练测试
基于两种参数(决策树深 max_depth、基树个数 n_estimators)的不同取值下集成学习的性能来进行分析,给出不同参数下测试集准确率组图如下:
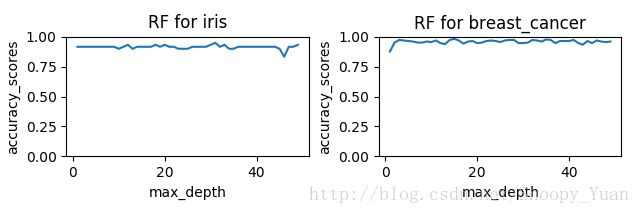
RF模型下 max_depth 参数对准确率的影响:
RF模型下 n_estimators 参数对准确率的影响:
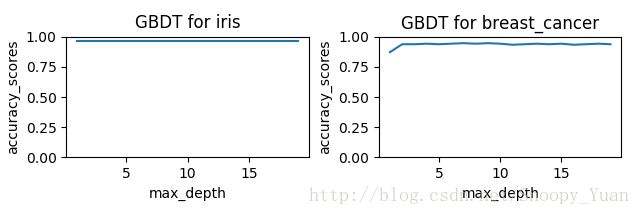
GBDT模型下 max_depth 参数对准确率的影响:
GBDT模型下 n_estimators 参数对准确率的影响:
从上面的系列图可以看出:
- 由于数据样本本身可分性良好,所以两种集成学习方法均表现出了极好的预测精度;
- 进一步地,在实验中我们发现,要达到相同的精度,RF要求的 max_depth 参数要比 GBDT 大,这是由于两种集成方法的偏差-方差侧重不同。
- 参数 n_estimator 越大,模型精度越高,但是模型训练耗时也越长,这是显而易见的;
小结与参考
本文回顾了集成学习的思路,并以RF、GBDT为典型进行了实验。由于此处选择的数据集并没有太大的规模,且总体来说可分性好,所以实验结果并没有明显地将RF、GBDT等方法的威力反映出来,但是,本文为两种算法的调参提供了思路,为进一步将这些方法用于复杂性问题积累了经验。
本文涉及到的一些重要参考链接如下:
- 基础知识: 博客 - 笔记︱集成学习Ensemble Learning与树模型、Bagging 和 Boosting
- 基础知识: 博客 - GBDT:梯度提升决策树
- 实现辅助: sklearn官网 - 集成学习API
- 实现辅助: sklearn官网 - Classifier comparison