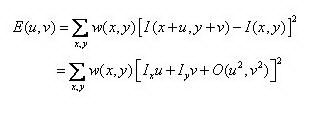图像算法之二：特征提取算法系列之Harris

Harris算子介绍：

该算子是C．Harris和M．J．Stephens在1988年提出的一种点特征提取算子。这种算子受信号处理中自相关函数的启发，可以给出图像中某一像素点的自相关矩阵肘，其特征值是自相关函数的一阶曲率，如果X，Y两个方向上的曲率值都高，那么就认为该点是角点。

Harris[2]角点检测算子是Moravec角点检测算子的改进.

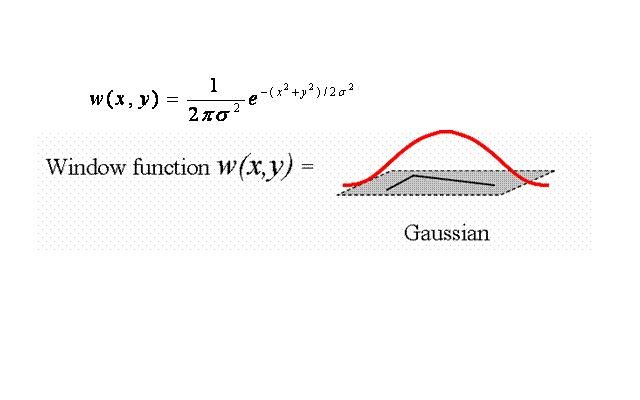
（1）算子用高斯函数代替二值窗口函数,对离中心点越近的像素赋于越大的权重，以减少噪声影响。

                    图1-3高斯函数

(2)Moravec算子只考虑了每隔45度方向，Harris算子用Taylor展开去近似任意方向。

写成矩阵形式: :

式子（1-2）

式子（1-3）
式中，Ix为x方向的差分，Iy为y方向的差分，w(x,y)为高斯函数。

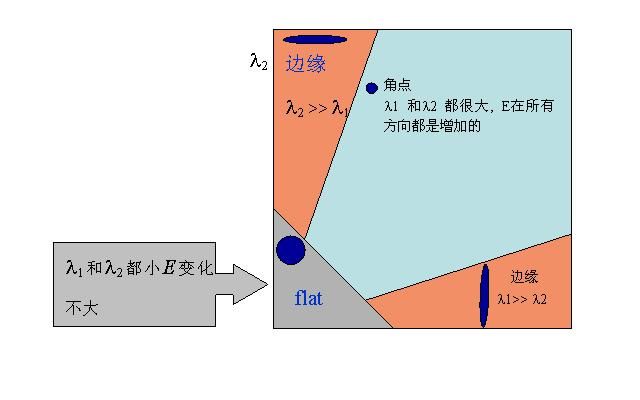
(3) Harris采用了一种新的角点判定方法。矩阵M的两个特征向量l1和l2与矩阵M的主曲率成正比。Harris利用l1, l2来表征变化最快和最慢的两个方向.若两个都很大就是角点,一个大一个小就是边缘,两个都小就是在变化缓慢的图像区域。

图1- 4用矩阵Ｍ的特征向量分类图像像素点

但是解特征向量需要比较多的计算量,且两个特征值的和等于矩阵M的迹，两个特征值的积等于矩阵M的行列式。所以用(1-4）式来判定角点质量。(k常取0.04-0.06)
（1-4）
(4) Harris算法总结

Step 1:对每一像素点计算相关矩阵M。

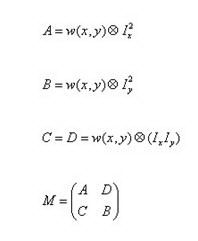
Step 2:计算每像素点的Harris 角点响应。

Step 3.在w*w范围内寻找极大值点，若Harris 角点响应大于阀值，则视为角点。

Harris算子对灰度的平移是不变的,因为只有差分，对旋转也有不变性，但是对尺度很敏感,在一个尺度下是角点, 在在另一个尺度下可能就不是了.

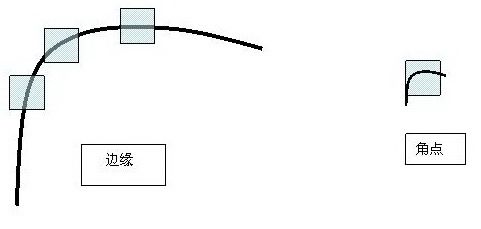
              图1- 5　harris算子对尺度的敏感性

             图1- 6　harris算子对简单图像的响应

Harris 算子是一种有效的点特征提取算子,其优点总结起来有:

①计算简单:Harris 算子中只用到灰度的一阶差分以及滤波,操作简单。

②提取的点特征均匀而且合理:Harris 算子对图像中的每个点都计算其兴趣值,然后在邻域中选择最优点。实验表明,在纹理信息丰富的区域,Harris 算子可以提取出大量有用的特征点,而在纹理信息少的区域,提取的特征点则较少。

③稳定:Harris算子的计算公式中只涉及到一阶导数，因此对图像旋转、灰度变化、噪声影响和视点变换不敏感,它也是比较稳定的一种点特征提取算子。

Harris 算子的局限性有：

  ①它对尺度很敏感，不具有尺度不变性。
  ②提取的角点是像素级的。

参考文献：
[1]Chris Harris, Mike Stephens, A Combined Corner and Edge Detector, 4th Alvey Vision Conference, 1988, pp147-151