VAE与GAN的关系(1)

VAE（Variational Auto-Encoder）和GAN（Ganerative Adversarial Networks）都是生成模型（Generative model）。所谓生成模型，即能生成样本的模型。我们可以将训练集中的数据点看作是某个随机分布抽样出来的样本，比如：MNIST手写体样本，我们就可将每一幅图像看作是一个随机分布 p(x) p ( x ) 的抽样（实例）。如果我们能够得到这样的一个随机模型，我们就可以无限制地生成样本，再无采集样本的烦恼。但这个随机分布 p(x) p ( x ) 我们并不知道，需要通过对训练集的学习来得到它，或者逼近它。要逼近一个随机分布，其基本思想是：将一个已知的，可控的随机分布 q(z) q ( z ) 映射到目标随机分布 p(x) p ( x ) 上。在深度学习领域中，有两个典型的生成模型：1、VAE，变分自编码器；2、GAN，生成对抗性网络，它们的结构如图1、图2：

图1 VAE结构图

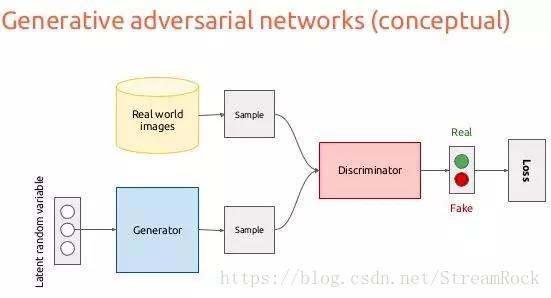
图2 GAN结构图
VAE的工作流程是：
1、在训练集（Dataset）中抽样，得到样本 xi x i ， xi x i 经过神经网络编码器（NN Encoder）得到一个正态分布（ N(μi,σ2i) N ( μ i , σ i 2 ) ）的充分统计量：均值（以图1为例进行解释， μi=(m1,m2,m3) μ i = ( m 1 , m 2 , m 3 ) ）和方差（ σi=(σ1,σ2,σ3) σ i = ( σ 1 , σ 2 , σ 3 ) ）；
2、由 N(μi,σ2i) N ( μ i , σ i 2 ) 抽样得到 zi z i ， 已知 zi z i 的分布是标准正态分布 N(0,1) N ( 0 , 1 ) ；
3、 zi z i 经过NN_Decoder得到输出 x̂i x ^ i
4、 Loss=‖x̂i−xi‖ L o s s = ‖ x ^ i − x i ‖ ，训练过程就是让Loss取得最小值。
5、训练好的模型，我们可以利用Decoder生成样本，即将已知分布 q(z) q ( z ) 的样本通过Decoder映射成目标 p(x) p ( x ) 分布的样本。
以上过程可以用图3进行概括。

图3 VAE原理图
为比较VAE和GAN的差异，参考图4，简述GAN的工作原理如下：
1、在一个已知的、可控的随机分布 q(z) q ( z ) (e.g.:多维正态分布 q(z)=N(μ,σ2) q ( z ) = N ( μ , σ 2 ) )采样，得到 zi z i ；
2、 zi z i 经过生成器映射 G(zi) G ( z i ) 得到在样本空间（高维空间）的一个数据点 xgi x i g ，有 xgi=G(zi) x i g = G ( z i ) ；
3、 xgi x i g 与样本流型（Manifolds）之间的距离在图中表示为 D(‖xgi,x̂gi)=‖xgi−x̂gi‖ D ( ‖ x i g , x ^ i g ) = ‖ x i g − x ^ i g ‖ ，其中 x̂gi x ^ i g 表示 xgi x i g 在流型上的投影，生成器的目标是减少此距离，可以将此距离定义为生成器的损失（Loss）。
4、因为不能直接得到样本的流型，因而需要借助判别器(Discriminator)间接地告诉生成器（Generator）它生成的样本距样本流型是“远了”还是“近了”，即判别真（real）和假（fake）正确的概率，一方面要判别器提高判别准确性，一方面又要提高生成器的以假乱真的能力，由此形成了竞争导致的均衡，使判别器和生成器两者性能同时提高，最后我们可获得最优的生成器。
5、理想的最优生成器，能将生成的 xgi x i g 映射到样本分布的流型中（即图中阴影部分）

图4 GAN原理
由GAN的生成过程，我们可以很直观地得到两个GAN缺陷的解释（详细分析可见《Wasserstein GAN》）：
1、模型坍塌（Model collapse）
GAN只要求将 xgi x i g 映射至离样本分布流型尽可能近的地方，却不管是不是同一个点，于是生成器有将所有 zi z i 都映射为一点的倾向，于是模型坍塌就发生了。
2、不收敛
由于生成器的Loss依赖于判别器Loss后向传递，而不是直接来自距离 D(xgi,x̂gi) D ( x i g , x ^ i g ) ，因而若判别器总是能准确地判别出真假，则向后传递的信息就非常少（体现为梯度为0），则生成器便无法形成自己的Loss，因而便无法有效地训练生成器。正是因为这个原因，《Wasserstein GAN》才提出了一个新的距离定义（Wasserstein Distance）应用于判别器，而不是原型中简单粗暴的对真伪样本的分辨正确的概率。Wasserstein Distance所针对的就是找一个方法来度量 D(xgi,x̂gi) D ( x i g , x ^ i g ) 。

比较VAE与GAN的效果，我们可以得到以下两点：
1、GAN生成的效果要优于VAE
2、GAN比VAE要难于训练

文章：Variational Inference: A Unified Framework of Generative Models and Some Revelations，原文：arXiv:1807.05936，中文链接：https://kexue.fm/archives/5716。文章来自中山大学 数学学院 苏剑林。文中为两个生成模型建立了统一的框架，并提出一种为训练Generator而设计的正则项原理，它可以作为《Wasserstein GAN》的一个补充，因为WGAN给出的是GAN判别器Loss的改进意见，而该文却是对生成器下手，提出生成器的一个正则项原则。
以下是从变分推断（Variational Inference）角度对两个模型的推导过程：
p(x) p ( x ) 是真实随机变量的分布，样本集中的数据可认为是从这个分布中抽样出来的样本，它是未知的。我们希望用一个可控的、已知的分布 q(x) q ( x ) 来逼近它，或者说让这两个分布尽量重合。如何实现这个目标呢？一个直观的思路是：从一个已知的分布出发，对其中的随机变量进行映射，得到一个新的分布，这个映射后分布与目标分布尽量重合。在VAE中，这个映射由Decoder完成；在GAN中，这个映射由Generator来完成。而已知分布可以是：均匀分布或正态分布，例如：随机变量 z z 服从多维标准正态分布 z∼N(0,1) z ∼ N ( 0 , 1 ) ，它经过映射得到 xgi x i g ，为表述方便我们统一用 G(zi)=xgi，xgi∼q(x) G ( z i ) = x i g ， x i g ∼ q ( x ) 表示经过映射后的随机变量 xg x g 服从分布 q(x) q ( x ) ，它与真实变量分布 xr∼p(x) x r ∼ p ( x ) 在同一个空间 X X 。我们希望得到尽可能与 p(x) p ( x ) 重合的 q(x) q ( x ) 。
为达到“尽量”这一目标，需要对重合程度进行量化，于是我们定义了一个测度的指标——KL散度：

KL(p(x)‖q(x))=∫p(x)logp(x)q(x)dx(1) K L ( p ( x ) ‖ q ( x ) ) = ∫ p ( x ) log ⁡ p ( x ) q ( x ) d x ( 1 )

当p(x)与q(x)完全重合，有 KL(p(x)‖q(x))=0 K L ( p ( x ) ‖ q ( x ) ) = 0 ，否则 KL(p(x)‖q(x))>0 K L ( p ( x ) ‖ q ( x ) ) > 0 。直接求上述真实分布 p(x) p ( x ) 与生成分布 q(x) q ( x ) 的KL散度 KL(p(x)‖q(x)) K L ( p ( x ) ‖ q ( x ) ) 有时十分困难，往往需要引入隐变量（Latent Variables）构成联合分布 p(x,z) p ( x , z ) 和 q(x,z) q ( x , z ) ，计算 KL(p(x,z)‖q(x,z)) K L ( p ( x , z ) ‖ q ( x , z ) ) 来代替直接计算 KL(p(x)‖q(x)) K L ( p ( x ) ‖ q ( x ) ) 。
（1）GAN的联合分布 p(x,z) p ( x , z ) 的拟合
GAN在Generator生成了 xgi x i g 将与真实样本 xri x i r 一起作为输入 x x ，进入一个二选一选择器，该选择器以一定的概率（比如说50%）选择其一（选择器可以看成是随机变量 y y ，它服从服从0-1分布）, x x 接着进入判决器，判决器判定输入 x x 的是真实样本（ xr x r ），判断为1，或是生成样本（ xg x g ），判断为0，最后输出给定 x x 判为1的概率。
令联合分布是输入 x x 和选择器 y y 的分布， p(x,y) p ( x , y ) 表示真实的联合分布，而 q(x,y) q ( x , y ) 是判别器可控制的联合分布，是为拟合真实分布所设计的分布，由上机制可见，在 q(x,y) q ( x , y ) 中， x x 与 y y 其实是相互独立的，因而有：

q(x,y)={p(x)⋅p1q(x)⋅p0if y=1 if y=0 (2) q ( x , y ) = { p ( x ) ⋅ p 1 if  y = 1   q ( x ) ⋅ p 0 if  y = 0   ( 2 )

其中， p1 p 1 表示 y=1 y = 1 的概率， p0 p 0 表示 y=0 y = 0 的概率，有 p1+p0=1 p 1 + p 0 = 1 。若判别器有足够的拟合能力，并达到最优时，则 q(x,y)→p(x,y) q ( x , y ) → p ( x , y ) ，这意味着：

q(x)=∑yq(x,y)→∑yp(x,y)=p(x)(3) q ( x ) = ∑ y q ( x , y ) → ∑ y p ( x , y ) = p ( x ) ( 3 )

为拟合，由（2）可得两个联合分布KL散度：

KL(q(x,y)‖p(x,y))=∫[ p(x)⋅p1logp(x)p1p(y=1|x)p(x)+q(x)⋅p0logq(x)p0p(y=0|x)p(x)] dx(4) K L ( q ( x , y ) ‖ p ( x , y ) ) = ∫ [   p ( x ) ⋅ p 1 log ⁡ p ( x ) p 1 p ( y = 1 | x ) p ( x ) + q ( x ) ⋅ p 0 log ⁡ q ( x ) p 0 p ( y = 0 | x ) p ( x ) ]   d x ( 4 )

令 p1=p0=0.5 p 1 = p 0 = 0.5 ，以 KL(q(x,y)‖p(x,y)) K L ( q ( x , y ) ‖ p ( x , y ) ) 为Loss，因为 p1 p 1 、 p0 p 0 、 p(x) p ( x ) 、 q(x) q ( x ) 与判别器参数无关，另外，判别器的输出是 p(y=1|x)=D(x) p ( y = 1 | x ) = D ( x ) ，因而：

KL(q(x,y)‖p(x,y))∼∫p(x)log1p(y=1|x)dx+∫q(x)log1p(y=0|x)dx=∫p(x)log1D(x)dx+∫q(x)log11−D(x)dx=−Ex∼p(x)(logD(x))−Ex∼q(x)(log(1−D(x)))(5) K L ( q ( x , y ) ‖ p ( x , y ) ) ∼ ∫ p ( x ) log ⁡ 1 p ( y = 1 | x ) d x + ∫ q ( x ) log ⁡ 1 p ( y = 0 | x ) d x = ∫ p ( x ) log ⁡ 1 D ( x ) d x + ∫ q ( x ) log ⁡ 1 1 − D ( x ) d x = − E x ∼ p ( x ) ( log ⁡ D ( x ) ) − E x ∼ q ( x ) ( log ⁡ ( 1 − D ( x ) ) ) ( 5 )

GAN的判别器要尽量分辨两个分布，因而要KL散度尽可能大，因而若(5)式要作为判别器的Loss，则需取反，即：

LossD=Ex∼p(x)(logD(x))+Ex∼q(x)(log(1−D(x)))(6)D=argminD[Ex∼p(x)(logD(x))+Ex∼q(x)(log(1−D(x)))](7) L o s s D = E x ∼ p ( x ) ( log ⁡ D ( x ) ) + E x ∼ q ( x ) ( log ⁡ ( 1 − D ( x ) ) ) ( 6 ) D = arg ⁡ min D [ E x ∼ p ( x ) ( log ⁡ D ( x ) ) + E x ∼ q ( x ) ( log ⁡ ( 1 − D ( x ) ) ) ] ( 7 )

（6）式与传统GAN判别器Loss分析结果（可参见: https://blog.csdn.net/StreamRock/article/details/81096105）相同。
讨论完判别器Loss_D，接下来讨论生成器的Loss_G，同样从（4）式入手，此时可调的参数是生成器的参数， p1 p 1 、 p0 p 0 、 p(x) p ( x ) 、 p(y=1|x) p ( y = 1 | x ) (即 D(x) D ( x ) )与生成器参数无关，与之相关的是 q(x) q ( x ) ，因而有：

KL(q(x,y)‖p(x,y))=∫[ p(x)⋅p1logp(x)p1p(y=1|x)p(x)+q(x)⋅p0logq(x)p0p(y=0|x)p(x)] dx∼∫q(x)logq(x)(1−D(x))p(x)dx(8) K L ( q ( x , y ) ‖ p ( x , y ) ) = ∫ [   p ( x ) ⋅ p 1 log ⁡ p ( x ) p 1 p ( y = 1 | x ) p ( x ) + q ( x ) ⋅ p 0 log ⁡ q ( x ) p 0 p ( y = 0 | x ) p ( x ) ]   d x ∼ ∫ q ( x ) log ⁡ q ( x ) ( 1 − D ( x ) ) p ( x ) d x ( 8 )

最优判决器应该具有如下特性：

D(x)=p(x)p(x)+q(x)(9) D ( x ) = p ( x ) p ( x ) + q ( x ) ( 9 )

（9）式可以从图5，直接得到。

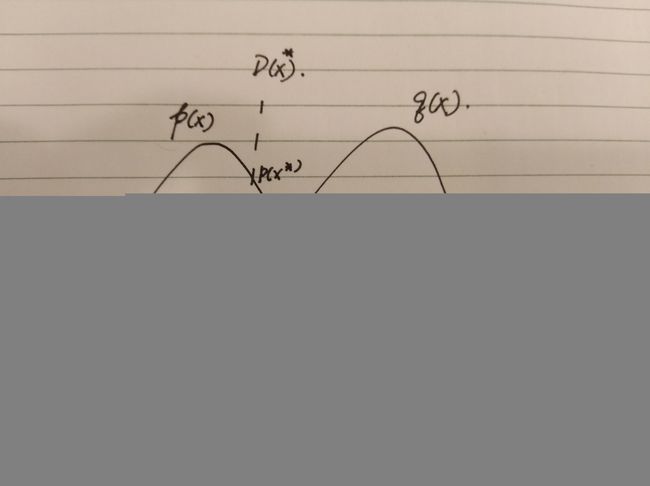
图5 最优判决器
将（9）代入（8）有：

Loss_G=∫q(x)logq(x)(1−D(x))p(x)dx=∫q(x)logq(x)(1−p(x)p(x)+q(x))p(x)dx=∫q(x)log1p(x)p(x)+q(x)dx=−∫q(x)logD(x)dx=−Ex∼q(x)(logD(x))=−Ez∼N(0,1)(logD(G(z)))(10) L o s s _ G = ∫ q ( x ) log ⁡ q ( x ) ( 1 − D ( x ) ) p ( x ) d x = ∫ q ( x ) log ⁡ q ( x ) ( 1 − p ( x ) p ( x ) + q ( x ) ) p ( x ) d x = ∫ q ( x ) log ⁡ 1 p ( x ) p ( x ) + q ( x ) d x = − ∫ q ( x ) log ⁡ D ( x ) d x = − E x ∼ q ( x ) ( log ⁡ D ( x ) ) = − E z ∼ N ( 0 , 1 ) ( log ⁡ D ( G ( z ) ) ) ( 10 )

于是可采用（10）作为生成器的损失Loss_G，与传统推导的结果一致。考察（9）式，式中 q(x) q ( x ) 实际上是不断变化的，因而我们将(9)改造一下， q0(x) q 0 ( x ) 表示前一次生成器的状态，于是有：

D(x)=p(x)p(x)+q0(x)(11)Loss_G=∫q(x)logq(x)(1−D(x))p(x)dx=∫q(x)logq(x)(1−p(x)p(x)+q0(x))p(x)dx=∫q(xlogq(x)D(x)q0(x)dx)=−Ex∼q(x)[logD(x)]+KL(q(x)‖q0(x))=−Ez∼N(0,1)[logD(G(z))]+KL(q(x)‖q0(x))(12) D ( x ) = p ( x ) p ( x ) + q 0 ( x ) ( 11 ) L o s s _ G = ∫ q ( x ) log ⁡ q ( x ) ( 1 − D ( x ) ) p ( x ) d x = ∫ q ( x ) log ⁡ q ( x ) ( 1 − p ( x ) p ( x ) + q 0 ( x ) ) p ( x ) d x = ∫ q ( x log ⁡ q ( x ) D ( x ) q 0 ( x ) d x ) = − E x ∼ q ( x ) [ log ⁡ D ( x ) ] + K L ( q ( x ) ‖ q 0 ( x ) ) = − E z ∼ N ( 0 , 1 ) [ log ⁡ D ( G ( z ) ) ] + K L ( q ( x ) ‖ q 0 ( x ) ) ( 12 )

比较（10）与（12）发现(12)多了一项 KL(q(x)‖q0(x)) K L ( q ( x ) ‖ q 0 ( x ) ) ,此为生成器Loss的正则项，它要求 q(x) q ( x ) 与 q0(x) q 0 ( x ) 尽可能小，由此可实现生成器的正则项，详细分析可见： https://kexue.fm/archives/5716