Deep Multi-View Spatial-Temporal Network for Taxi Demand Prediction
1.背景
这篇文章是滴滴出现发表在AAAI2018会议上的文章,其目的是通过历史订单数据来预测下一时刻城市中区域 i i i的订单量,也就是demand prediction。在论文的摘要部分作者说到:传统的demand prediction methods 通常都是从时序的角度来进行建模处理而忽略了复杂的时空间的非线性依赖关系。因此这篇文章采用了从多视角(Spatial View, Temporal View, Semantic View)的角度来对问题进行建模处理。
在论文的Introduction部分,作者进一步指出先前(例如ST-ResNet等)的方法都没能同时地考虑时间时间和空间上的依赖关系(到底这么才叫同时呢?)。所以作者采用了CNN+LSTM的方式来处理复杂的非线性时空依赖关系。但是又不能直接照搬ST-ResNet中的卷积方式(将整个城市看成是一张image,然后对整个image进行卷积操作),因为作者认为 “ near things are more related than distant things " ,因此作者采用了局部卷积(local CNN)的做法。 仔细想想也有道理,因为订单数据不同于人流数据。在ST-ResNet中,作者说到之所以要采用那样的卷积方式,是因为考虑到即使两个相距很远的区域依然很有可能出现人口的流入流出(如某地举办大型活动),而对于订单数据来说则更倾向于邻近区域之间的相互影响。
接着作者又指出,由于采用了local CNN使得存在这样的可能性:尽管在立体空间上相距较远的区域,在语义空间中可能有着类似的需求模型。例如,"For example, residential areas may have high demands in the morning when people transit to work, and commercial areas may be have high demands on weekends. " 作者举出这个例子是为了说明,尽管住宅区和商业区相距很远,但是从两者的需求模型(住宅区早上和商业区周末)来看却有着相似性。为了解决这一问题,作者又引出了第三个视角Semantic View。
temporal view: 通过LSTM来建模时间维度上的依赖性;
spatial view: 通过local CNN 来建模局部空间上的依赖性;
semantic view: 通过graph embedding来建模具有相似需求模型的地区;
2. 网络模型
2.1 数据处理及问题定义
-
同ST-ResNet中的处理方式一样,首先将整个城市划分成若干个互不相交的矩形区域 l i l_i li,且 L = { l 1 , l 2 , ⋯ , l N } L=\{l_1,l_2,\cdots,l_N\} L={l1,l2,⋯,lN};同时,时间序列集合 L = { I 0 , I 1 , ⋯ , I T } \mathcal{L}=\{I_0,I_1,\cdots,I_T\} L={I0,I1,⋯,IT},设置时间片的大小为30分钟
-
将一个请求订单 o o o定义为一个三元组: ( o . t , o . l , o . u ) (o.t,o.l,o.u) (o.t,o.l,o.u),分别表示时间戳、区域位置和乘客编号;
-
将区域 l i l_i li在 t t t时刻的订单量定义为: y t i = { o : o . t ∈ I t ∧ o . l ∈ l i } y^i_t=\{o:o.t\in I_t \wedge o.l \in l_i\} yti={o:o.t∈It∧o.l∈li},也就是某个时间片 I i I_i Ii内,在区域 l i l_i li中的所有订单数
-
将 t t t时刻,区域 l i l_i li中的环境特征(例如:温度、气象等)定义为 e t i ∈ R r \mathcal{e}^i_t\in\mathcal{R^r} eti∈Rr
-
将最终的预测问题定义为:
y t + 1 i = F ( Y t − h , . . . , t L , E t − h , . . . , t L ) ; i ∈ L y^i_{t+1}=\mathcal{F}(\mathcal{Y}^L_{t-h,...,t},\mathcal{E}^L_{t-h,...,t});\;\;i\in L yt+1i=F(Yt−h,...,tL,Et−h,...,tL);i∈L
其中 Y t − h , . . . , t L , E t − h , . . . , t L \mathcal{Y}^L_{t-h,...,t},\mathcal{E}^L_{t-h,...,t} Yt−h,...,tL,Et−h,...,tL分别表示所有区域中的历史订单量和历史环境信息,以此来预测区域 l i l_i li中下一时刻的订单量
2.2 Spatial View : Local CNN
作者之所以要提出用local CNN的原因在于,若对依赖关系较弱(相距较远)的区域进行卷积,会最终导致不好的结果,因此论文中采用了 local CNN。
We realize including regions with weak correlations to predict a target region actually hurts the performance. To address this issue, we propose a novel local CNN method which only considers spatially nearby regions. This local CNN method is motivated by the First Law of Geography: “near things are more related than distant things,”
Local CNN 和CNN实质上没有差别,只是在作用区域上Local CNN 并不是对整张image做卷积,而只是局部。
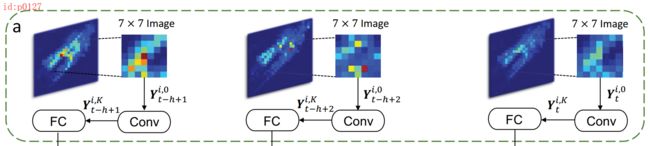
如图p0127所示,在 t t t时刻对于每一张image来说,以区域 i i i 为中心取宽度为 S S S的局部区域 Y t i ∈ R S × S × 1 Y^i_t\in\mathbb{R}^{S\times S\times 1} Yti∈RS×S×1(当区域 i i i位于image边缘时,用0填充)。接着,将 Y t i Y^i_t Yti(为了同后续卷积结果记法一致,文中用 Y t i , 0 Y^{i,0}_t Yti,0来表示)作为第一次卷积的输入;第 t t t时刻的输入在经过 K K K个卷积层后,输出结果为 Y t i , K ∈ R S × S × λ Y^{i,K}_t\in\mathbb{R}^{S\times S\times\lambda} Yti,K∈RS×S×λ, λ \lambda λ表示第 K K K层卷积核的个数,其中:
Y t i , k = f ( y t i , k − 1 ∗ W t k + b t k ) Y^{i,k}_t=f(y^{i,k-1}_t*W^k_t+b^k_t) Yti,k=f(yti,k−1∗Wtk+btk)
接下来,将 Y t i , K Y^{i,K}_t Yti,Kreshape成 s t i ∈ R S 2 λ s_t^i\in\mathbb{R}^{S^2\lambda} sti∈RS2λ作为下一个全连接层的输入,然后输出得到 s ^ t i ∈ R d \hat{s}^i_t\in\mathbb{R}^d s^ti∈Rd.
2.3 Temporal View : LSTM
在经过local CNN处理之后,对于任意时刻 t t t来说,都有一个输出 s ^ t t \hat{s}^t_t s^tt;接着,再将其与天气、事件等额外因素 e t i ∈ R r e^i_t\in\mathbb{R}^r eti∈Rr进行拼接,得到 g t i ∈ R r + d \mathbb{g}^i_t\in\mathbb{R}^{r+d} gti∈Rr+d;最后,将多个时刻的结果输入到标准的LSTM当中来拟合时间维度上的依赖关系,最终输出 h t i h^i_t hti

2.4 Semantic View : Graph Embedding
由于作者前面说到整个网络结构将以local CNN的形式进行空间维度上的特征提取,而由此带来的问题便是有的区域之间虽然相隔很远,但是在需求模型上可能一样。(虽然看起来同使用local CNN的初衷有点违背,但按照作者的意图来看是想做到:总体上采用local CNN,对于这种特殊情况采用其它方法来解决)因此,作者提出采用基于需求模型相似性的区域图结构来捕捉这种潜在的语义信息,听起来有点拗口,具体做法如下:
We propose to use a graph of regions to capture this latent semantic, where the edge represents similarity of demand patterns for a pair of regions.

其具体做法就是,首先以所有的区域为顶点,各区域之间的相似度为权重构造一个无向图;而所谓的相似度就是根据DTW算法计算任意两个区域需求模型的相似度。如图p0129左边所示第二个小图所示,上下分别为不同区域在各个时刻的需求量,而根据DTW算法就可以求得两者的相似度。
在得到这个带权无向图之后,根据图嵌入(graph embedding )方法得到每个区域的向量表示 m i m^i mi(类似于词向量中每个词的向量表示)。对于 m i m^i mi的理解,由于 m i m^i mi表示的是区域 i i i的需求模型,因此对于越是需求模型相似的区域,其向量表示越相近距离越小。这样一来,对于有着相似需求模型的区域来说, m i m^i mi所施加的影响就越相似。
最后,将 m i m^i mi经过一个全连接层后输出 m ^ i \hat{m}^i m^i,并与 h t i h^i_t hti进行拼接得到 q t i q^i_t qti,然后是最后的全连接层预测输出得到 y ^ t + 1 i \hat{y}^i_{t+1} y^t+1i
另外值得说的一点就是,论文中的损失函数不仅有通常的平方误差项,还增添了额外的一个“占比”项。用以避免较大(或较小)的预测值对结果的影响。
L ( θ ) = ∑ i = 1 N ( ( y t + 1 i − y ^ t + 1 i ) 2 + γ ( y t + 1 i − y ^ t + 1 i y t + 1 i ) 2 ) \mathcal{L}(\theta)=\sum_{i=1}^{N}\left(\left(y_{t+1}^{i}-\hat{y}_{t+1}^{i}\right)^{2}+\gamma\left(\frac{y_{t+1}^{i}-\hat{y}_{t+1}^{i}}{y_{t+1}^{i}}\right)^{2}\right) L(θ)=i=1∑N((yt+1i−y^t+1i)2+γ(yt+1iyt+1i−y^t+1i)2)
The loss function consists of two parts: mean square loss and square of mean absolute percentage loss. In practice, mean square error is more relevant to predictions of large values. To avoid the training being dominated by large value samples, we in addition minimize the mean absolute percentage loss.
3.总结
论文以逐个区域分开的方式来进行需求预测,可以算上是piexl-level层面的做法,这种做法也值得借鉴;同时,论文中还引入了一种新的语义视角来建模具有相似需求模型的小区域,这种思路也很新颖。
参考:
动态时间规整—DTW算法
深度学习中不得不学的Graph Embedding方法
流量预测相关 交流群: 883638095
