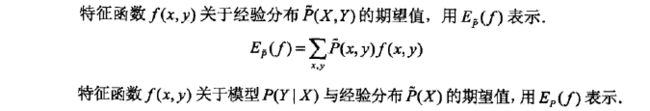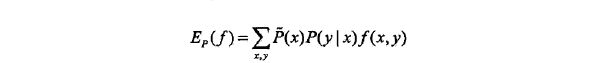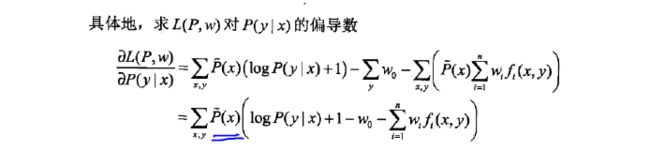一些对最大熵模型的理解

一、最大熵原理

概念：对于随机变量X，其概率分布为P(X)，一般在约束条件下会有无数P(X)存在。最大熵原理就是在所有符合约束条件的P(X)中，熵最大的模型即为最优模型。

二、最大熵模型

最大熵模型，就是基于最大熵原理的分类模型。李航《统计学习方法》中对最大熵模型的描述如下：

问题1：为什么是条件熵？

因为我们需要的是一个分类模型，也就是对于样本x，模型返回其对应的类别y，即模型应该是一个条件概率分布，表示为P(Y|X)。

 

问题2：在最大熵模型定义中，式（6.12）究竟表示什么意思？为什么要引入这条约束条件？

（1）要理解这个问题，首先看式（6.12）等号的右侧部分定义。后面距离比较长，理解的同学就不必看了）：

也就是说，是特征函数f(x,y)的期望值，我们知道当x=y时，f(x,y)=1；否则f(x,y)=0。上面的公式表示，在训练集中，所有x和y可能组成的关系中，满足特征函数f(x,y)=1的数量。

打个比方，你统计女人喜欢或不喜欢某个男人的原因。回答肯定有很多种，我们用变量x表示喜欢或不喜欢的原因，变量y表示喜欢或不喜欢。有女孩认为喜欢的原因是“他很帅气”，此时事实就是“x=帅，y=喜欢”，我们定义特征函数f(x=帅，y=喜欢)=1来表示这样一个事实；但有的哥们就悲剧了，姑娘不喜欢的原因是认为他“穷”，此时事实就是“x=穷，y=不喜欢”，我们定义为特征函数f(x=穷,y=不喜欢)=1来表示。现在，我们假设走访了1000位女生，得到了1000个回答。就表示这1000个回答中，喜欢男生的原因是帅和不喜欢男生的原因是因为穷的女生总数。

我这里只列举了两种事实，并假设通过这两种事实就能很好地描述我走访的这1000个女生的回答（也就是假设大部分女生都是这两种回答）。由此可以看出，我们可以定义很多事实来描述给定的训练集，好的事实更能得到好的模型，所以训练最大熵模型时，确定好符合训练集的事实很重要。比如上面的例子中，最好不要定义类似这样的事实“x=按时吃饭，y=喜欢”，因为你觉得在回答喜欢的女生中，会有多少是因为“按时吃饭”这个原因喜欢男生的？本质原因是这样的事实不能很好地描述已知数据集。

这个期望值衡量的是什么呢？其实就是衡量你定义的这些个特征函数（本质上表示x和y满足某一事实），对已知事实（即训练集）的描述程度。

（2）再看等式（6.12）左边的部分，是不是发现很相似呢？它也是一个期望：

和右边公式的差别就是右边公式中的变成了。为什么会是这样？其实我们也不想这样，我们也想获得x和y的联合概率分布，但我们是不知道的，只能另想办法。办法就是根据全概率公式，我们只要知道即可。但我们也不知道，进死胡同了吗？没有，好在我们知道啊。根据大数定律，在样本达到一定数量后，我们可以用经验分布来表示真实的概率分布，这样就可以表示啦。

（3）这两个期望和相等，有什么意义？

根据（1）中的举例，其实就是为了描述女生喜欢或不喜欢男生的原因的分布情况，我定义了n个事实，相应的有n个特征函数。由于不可能去统计地球上所有女生的回答，因此我希望调研的1000个女生中的原因分布与真实情况下的分布最接近，理想的情况是相同！注意，和都是小于1的，因为本质上，其中x和y满足某一事实。而对所有x，y，有。同理对于也是一样。

 

问题3：为什么公式中有个?

按照熵的定义，公式中应该没有。个人认为是为了方便后面学习过程的推导（见下面的公式），如果没有这个参数，下面公式最后一项中的就提取不出来，就会造成在最后的模型中存在参数，而不一定是准确的。

那为什么乘上没关系呢？因为对于给定的训练数据集，是一个常数，因此对于后面最大熵模型的极大似然估计是没有影响的。

三、最大熵模型的学习

这部分难点是将约束最优化问题转换为无约束最优化的对偶问题。

关于拉格朗日乘子法，这里就不再叙述了，不理解的同学可以参考https://www.zhihu.com/question/38586401，其中@戏言玩家解释的很好。

下面讲讲我对转换的理解，请看书中公式：

对于为什么会有公式（6.18）应该没有问题吧？

（6.18）可以这样理解：先给定某种模型（，其中C是模型空间），然后在参数空间{w}中，找到某个，得到的最小值。一个模型对应一个最小值，求所有模型中的最小值就是,i=1,2,...,k(C)，k(C)表示模型空间中的模型数量。

很好，公式本身的逻辑没有问题。问题在于公式中L(P,w)是凸函数，其图像也就是类似。凸函数有极小值，但可能没有最大值，即最大值可能是正无穷（无约束或即使在某些约束条件下）。因此不能保证凸函数的max值存在且能求出。那怎么办呢？那就把上面求的过程反过来吧，也就是转化为公式（6.18）的对偶问题，表示为公式（6.19）。

那么就来说说我对公式（6.19）的理解。我们先固定住w，就可以表示为给定w时，约束曲线与模型P的等高线的最低相切点（如下图，红色曲线为约束曲线g(x,y)，图来自知乎，见上面给的链接。另外，其实应该是约束平面而不是曲线，因为g(x,y)=K），而表示求所有模型的最低相切点中，值最小的那个切点。现在解绑w，每个w都有一个这样的切点，那么我们求所有w中最大的那个切点，也就是公式（6.19）。

这样的一个点能够使所有不满足约束条件的点都在该点之下（也就是只要该点之上的点都满足约束条件）。这个时候的就是拉格朗日函数中的H(P)，也就是所求最大熵模型。需要注意的是，公式（6.19）的值≥公式（6.18）的值。

（图片来自知乎）

四、为什么要求对偶函数的极大化？

书中有一句话，不知道大家注意到没有：

为什么会有这个结论？其实，约束最优化问题（6.14）~（6.16）转换为无约束最优化的对偶问题后，求解约束最优化问题就变成了对偶函数的极大化，而对偶函数的极大化是与最大熵模型的极大似然估计等价的（证明如书中第87页）。最大熵模型的极大似然估计不就是要求解的P(y|x)吗？