机器人找金币------一个经典的强化学习实验

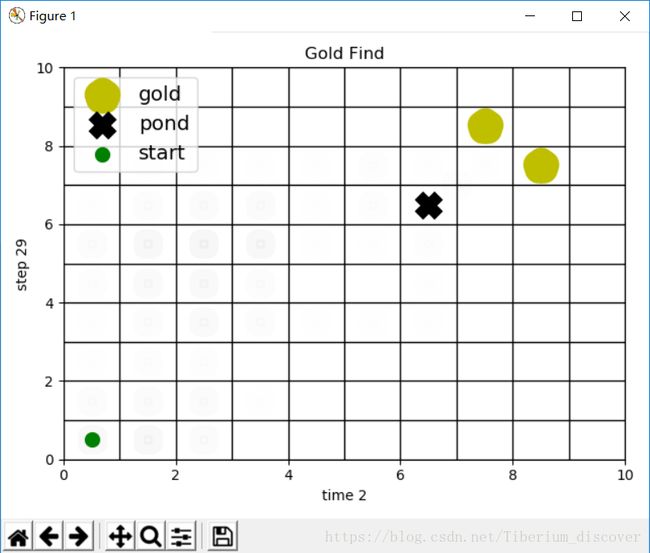
代码之前：这是在电子科大面试（实习）时老师布置的任务，过去学习的基本上是统计学习方法，从来没有接触过强化学习的相关内容，因此走了不少弯路。先简要描述一下问题：在一个十乘十的方格中有一个机器人寻找金币。有一个金矿和水坑分布在该方格处，机器人需要寻找到金币并尽力避开水坑。开始时机器人位于左下角处随机搜索，遇到金币或者水坑后停止搜索，利用强化学习不断迭代逐渐使得机器人找到最优路径。（截图显示的是两个金币矿的时候）

第一次的思路特别简单，也被批评了。利用一个十乘十的矩阵记录每一个方格点（状态）的权值，初始均为零。在一次迭代后（一轮寻找过程），若寻找到金币，则为路径上每一个方格点的权值加上一个正值（越靠近金币增加权值越多），若寻找到水坑，则为路径上每一个方格点的权值增加一个负值。例如：走过了1（-1），2（-1），3（-1），4（+5）四个路径点，最终在4点处找到了金币，则为3号节点增加权值4（5-1），2号节点增加权值3（5-1-1），1号节点增加权值2（5-1-1-1）。在机器人每一次择路过程（选择下一次的状态）中，均以百分之八十的几率选择临近节点中权值最大的节点作为下一个状态（贪婪），以百分之二十的几率随机选择任一临近节点作为下一个状态（探索）。这就是第一次实验的基本思路。这种算法存在许多的问题，比如根本没有用到强化学习中的贝尔曼方程，对于回报、值函数等概念也难有定义。（这里就不再贴代码了，也烦请各位大神指正）
后来在学长的指导下，初步了解了一下SARSA算法，回到家后，购买了一本《深入浅出强化学习原理入门》，在这里不得不吐槽一下本书，十分不友好。感觉作者是不是对“人人都可以读懂”“老妪能解”这些词语有什么误解。反正看起来比较艰辛，对比李航老师的《统计学习方法》一书确实是有较大的差距。

闲言少叙，SARSA学习方法是一种基于时间差分的强化学习方法，该方法除了考虑当前行为-值函数的影响，还要考虑下一步对当前状态的影响进而作出决定。（实质就是增加一个A，下一步的A，然后据此来估计Q(s,a)）其中最重要的是：（1）行为值函数的表示，（2）探索环境的策略以及（3）值函数更新。

（1）这一部分是行为—值函数，利用python中字典数据类型表示，机器人的状态有10x10个，考虑到边界以外是12x12个，动作集合一共有四个，上下左右。字典的索引由三部分构成，状态的横坐标，纵坐标，以及动作。键值为行为—值函数，初始均为0。

for i in range(-1,11):
    for j in range(-1,11):
        states_coordinate.append([i,j])

actions=['e','s','w','n']   #动作集合

qfunc=dict()    #初始化q函数值
for s in states_coordinate:
    for a in actions:
        key="%d-%d-%s"%(s[0],s[1],a)
        qfunc[key]=0.0

（2）另一部分是行动策略，这里我们采用简化的策略方法，即每一次决策都有百分之八十的可能性选择使值函数最大的抉择（贪婪），百分之二十随机选择行为（贪婪）

def greedy(qfunc,state):   #行动策略，传入q函数，当前状态，返回下一个状态
    r=random.uniform(0,1)
    amax=0
    qmax=qfunc["%d-%d-%s"%(state[0],state[1],actions[0])]
    if r<=explore_rate:                #贪心走法
        for i in range(len(actions)):
            q=qfunc["%d-%d-%s"%(state[0],state[1],actions[i])]
            if qmaxelse:                    #探索走法
        amax=random.choice([0,1,2,3])
    return actions[amax]

（3）这一部分是值函数更新部分，采用的TD（时间差分）更新方程（如下），其实对于这一部分我理解地不是很深刻，还需要多看看博客体会一下。

qfunc[key]=qfunc[key]+alpha*(R+gamma*qfunc[new_key]-qfunc[key])

算法的主要流程伪代码如下所示：

算法之外，老师的另一个要求是利用python实现界面设计，大概是能够看到机器人每次寻路然后最优路径的颜色逐渐加深。这一部分主要应用到了python中动态图画包matplotlib.animation的内容，对我而言也是一个全新的部分，简而言之其中最重要的就是如下的函数：

anim = FuncAnimation(fig, update, init_func=init_paiting(), frames=gen_num(), interval=50, repeat=False)

其中各参数含义：
#fig: 是我们创建的画布。

# 创建画布
    fig, ax = plt.subplots()
    plt.xlim(0, 10)
    plt.ylim(0, 10)
    fig.set_tight_layout(True)
    ax.set_title('Gold Find')

#update是我们每个时刻要更新图形对象的函数，其返回值就是每次都要更新的对象，告诉FuncAnimation在不同时刻要更新哪些图 形对象，传入的对象即是第四个参数frames。

def update(frame):   #更新画面函数
    label1 = 'time {0}'.format(frame[0])  #横坐标代表迭代次数
    label2 = 'step {0}'.format(len(frame[1])) #纵坐标代表每次迭代走过的长度
    for i in frame[1]:
        i[0]+=0.5     #加0.5是为了在每个方格中心表示
        i[1]+=0.5
        data.append(i)

    sca1.set_offsets(data)  # 关键：更新数据
    ax.set_xlabel(label1)
    ax.set_ylabel(label2)
    return sca1, ax        #每次更新的都是图中的散点以及横纵坐标标识

#init_func: 初始化函数。
#frames: 相当于时刻t，要模拟多少帧图画，不同时刻的t相当于animat的参数。
#interval: 刷新频率，毫秒。

在画图这部分中，大家具体可以查阅其他老师的csdn博客，里面有较为完整的解说和实例。如振裕老师的博客：
https://blog.csdn.net/suzyu12345/article/details/78338091?readlog

由于贴动图比较麻烦，给大家先看一看静态图，待我稍微研究下录屏剪切再做一个GIF效果图。

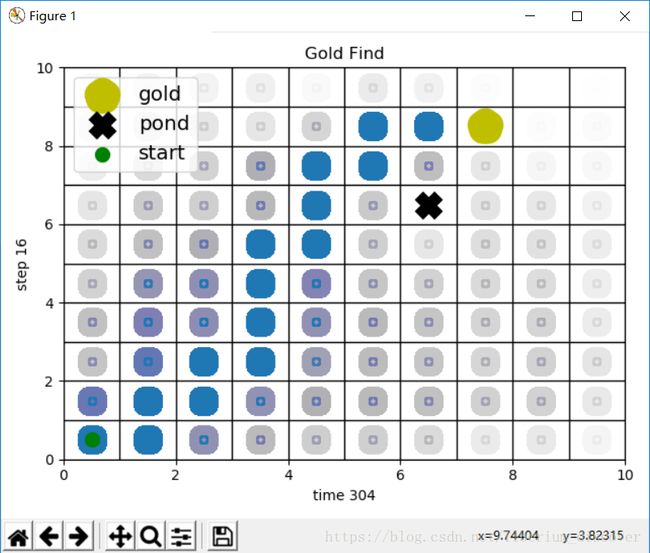
动态效果图如下所示：

现在就贴上完整代码，主函数给出注释，其余部分若有不理解欢迎留言讨论：

import numpy as np
import matplotlib.pyplot as plt
import random
import copy
from matplotlib.animation import FuncAnimation  # 动图的核心函数


alpha=0.1      #学习率
gamma=0.9      #遗忘因子
explore_rate=0.8   #探索率
gold_point = [] #初始化金币坐标点
gold_point.append([7,8])
#gold_point.append([8,7])
pond_point=[6,6]  #水池坐标点
states_coordinate=[]  #棋盘坐标


def init_paiting():

    # 画出一个维持不变的轴线。
    x_axis = []
    for i in range(0, 11):
        x_axis.append([i, i])
    y_axis = [11, 0]

    for i in range(len(x_axis)):
      line1 = ax.plot(x_axis[i],y_axis, 'k-', linewidth=1)  #横轴
      line2 = ax.plot(y_axis,x_axis[i],'k-', linewidth=1)     #纵轴

    gold1 = ax.scatter(gold_point[0][0] + 0.5, gold_point[0][1] + 0.5, c='y', marker='*', linewidth=20,label='gold')  # 金矿
    #gold2 = ax.scatter(gold_point[1][0] + 0.5, gold_point[1][1] + 0.5, c='y', marker='*', linewidth=20)
    pond = ax.scatter(pond_point[0]+0.5,pond_point[1]+0.5, c='k', marker='x', linewidth=20,label='pond')  # 水池
    point = ax.scatter( 0.5, 0.5, c='g', marker='o', linewidth=5,label='start')  # 起始点的散点图
    plt.legend(loc='upper left',fontsize='x-large')


for i in range(-1,11):
    for j in range(-1,11):
        states_coordinate.append([i,j])

actions=['e','s','w','n']   #动作集合

qfunc=dict()    #初始化q函数值
for s in states_coordinate:
    for a in actions:
        key="%d-%d-%s"%(s[0],s[1],a)
        qfunc[key]=0.0


def greedy(qfunc,state):   #行动策略，传入q函数，当前状态，返回下一个状态
    r=random.uniform(0,1)
    amax=0
    qmax=qfunc["%d-%d-%s"%(state[0],state[1],actions[0])]
    if r<=explore_rate:                #贪心走法
        for i in range(len(actions)):
            q=qfunc["%d-%d-%s"%(state[0],state[1],actions[i])]
            if qmaxelse:                    #探索走法
        amax=random.choice([0,1,2,3])
    return actions[amax]

def move(state,action):
    if action=='e':
        return [state[0]+1,state[1]]
    elif action=='s':
        return [state[0],state[1]-1]
    elif action=='w':
        return [state[0]-1,state[1]]
    elif action=='n':
        return [state[0], state[1]+1]

def gen_num():  #产生器函数
    for i in range(len(route_set)):
        yield [i,route_set[i]]


def update(frame):   #更新画面函数
    label1 = 'time {0}'.format(frame[0])
    label2 = 'step {0}'.format(len(frame[1]))
    for i in frame[1]:
        i[0]+=0.5
        i[1]+=0.5
        data.append(i)

    sca1.set_offsets(data)  # 关键：更新数据
    ax.set_xlabel(label1)
    ax.set_ylabel(label2)
    return sca1, ax


def compare_qfunc(qfunc1,qfunc2):   #比较两个值函数字典差异
    diff=0
    for key in qfunc1:
        diff+=abs(qfunc1[key]-qfunc2[key])
    print(n,diff)
    return diff


if __name__ == '__main__':
    # 创建画布
    fig, ax = plt.subplots()
    plt.xlim(0, 10)
    plt.ylim(0, 10)
    fig.set_tight_layout(True)
    ax.set_title('Gold Find')


    n=0      #迭代次数
    N=5000   #最大迭代次数
    route_set=[]   #路线集合列表，每迭代完一次将该路线加入路线集合
    error=10       #初始设置误差（可随机设置一个大数）

    while nand error>0.2:   #跳出迭代的条件：循环结束 or 前后两次值函数更新总和低于阈值
        n+=1
        state = [0, 0]     #机器人初始坐标点
        route = []         #本次迭代路线

        qfunc_old=copy.copy(qfunc)    #保存记录前一次值函数，方便比较误差

        while (True):  # 对于一次寻路过程
            oversize=False   #越界判断
            terminal=False   #终点判断
            take_action=greedy(qfunc,state)    #选择行动 a
            new_state=move(state,take_action)  #下一个状态 s'
            key="%d-%d-%s" % (state[0],state[1],take_action)
            route.append(state)   #将本次状态和行动记录入route

            if new_state[0]<0 or new_state[0]>9 or new_state[1]<0 or new_state[1]>9 :  #越界
                oversize = True
                R=-100       #回报-100
            elif new_state in gold_point:  #到达金矿
                terminal = True
                R=300        #回报+300
                route.append(new_state)
            elif new_state==pond_point:   #到达水坑
                terminal=True
                R=-100      #回报-100
                route.append(pond_point)
            else:                       #其余情况，每走一步回报-3
                terminal=False
                R=-3

            new_action = greedy(qfunc, new_state)    # 下一个状态，根据策略将采取的行动 a'
            new_key = "%d-%d-%s" % (new_state[0], new_state[1], new_action)

            qfunc[key]=qfunc[key]+alpha*(R+gamma*qfunc[new_key]-qfunc[key])
            state=new_state

            if (terminal or oversize):    #结束本次寻路条件，到达水坑或者金币（terminal）或者越界（oversize）
                break

        error=compare_qfunc(qfunc, qfunc_old)   #比较前后两次值函数误差总和
        if(oversize==False):
          route_set.append(route)           #若没有越界，则将本次线路加入到路线集合，方便在图中显示



    sca1 = ax.scatter([], [], alpha=0.005, marker='s', linewidths=15)
    data = []
    anim = FuncAnimation(fig, update, init_func=init_paiting(), frames=gen_num(), interval=50, repeat=False)
    plt.show()