leetCode刷题记录

1.minimum-depth-of-binary-tree

Given a binary tree, find its minimum depth.The minimum depth is the number of nodes along the shortest path from the root node down to the nearest leaf node.
使用广度优先搜索，类似层次遍历
我们把一层一层往下搜索，遇到第一个左右子树都为null，则返回dept

import java.util.LinkedList;
import java.util.Queue;
class TreeNode {
   int val;
   TreeNode left;
   TreeNode right;
   TreeNode(int x) { val = x; }
}
public class _14 {

    public static int run(TreeNode root) {
        if(root==null){
            return 0;
        }
        Queue queue=new LinkedList();
        queue.add(root);
        int dept=0;
        while (!queue.isEmpty()){
            ++dept;  //第i层
            int size=queue.size(); //第i层有多少个结点
            while (--size>=0){  //遍历节点 判断是否有左右子树都为null，有的话则直接返回结果。
                TreeNode current=queue.remove();
                if(current.left==null&¤t.right==null){
                    return dept;
                }
                if(current.left!=null){
                    queue.add(current.left);
                }
                if(current.right!=null){
                    queue.add(current.right);
                }
            }

        }
        return dept;
    }

    public static void main(String[] args) {
        TreeNode treeNode=new TreeNode(1);
        System.out.println(run(treeNode));
    }
}

2.evaluate-reverse-polish-notation

Evaluate the value of an arithmetic expression in Reverse Polish Notation.
Valid operators are+,-,*,/. Each operand may be an integer or another expression.
Some examples:
[“2”, “1”, “+”, “3”, ““] -> ((2 + 1) 3) -> 9
[“4”, “13”, “5”, “/”, “+”] -> (4 + (13 / 5)) -> 6
思路：逆波兰表达式，用一个栈模拟就可以了，遇到数字压入栈，遇到op，则弹出
两个值进行运算，再把结果压人栈中即可。

import java.util.*;
public class _16 {

    private static int Evaluate(int a,int b,String op){
        if(op.equals("+")){
            return a+b;
        }else if(op.equals("-")){
            return a-b;
        }else if(op.equals("*")){
            return a*b;
        }else{
            return a/b;
        }
    }

    public static int evalRPN(String[] tokens) {
        Stack st=new Stack();
        st.push(Integer.parseInt(tokens[0]));
        int ed=tokens.length;
        int s=0;
        String[] temp="+ - / *".split("\\s+");
        Vector vec=new Vector();
        vec.addAll( Arrays.asList(temp));
        int res=0;
        while (!st.isEmpty()){
            if(s1) {
                if (vec.contains( tokens[++s] )) {
                    int b = st.pop();
                    int a = st.pop();
                    st.push( Evaluate( a, b, tokens[s] ) );
                } else {
                    st.push( Integer.parseInt( tokens[s] ) );
                }
            }else{
                res=st.pop();
            }
        }
        return res;
    }

    public static void main(String[] args) {
        String[] res={"4", "13", "5", "/", "+"};
        System.out.println(evalRPN(res));
    }
}

3.word-break-ii

Given a string s and a dictionary of words dict, add spaces in s to construct a sentence where each word is a valid dictionary word.
Return all such possible sentences.
For example, given
s =”catsanddog”,
dict =[“cat”, “cats”, “and”, “sand”, “dog”].
A solution is[“cats and dog”, “cat sand dog”].
思路：
用一个数组dp[i][j]表示第i位到第(i+j)位是否存在dict里面的单词。
例如dp[0][2]就表示cat,dp[0][3]表示cats.保存所有状态值，匹配为1，不匹配为0.
我们利用深搜找出所有的情况即可。

public class _17 {

    private static int[][] dp;
    private static ArrayList result;

    public static ArrayList wordBreak(String s, Set dict) {
        int len=s.length();
        dp=new int[len+1][len+1];
        for (int i=0;ifor (int j=0;j//表示偏移量
                dp[i][j]=check(s.substring(i,i+j+1),dict);
            }
        }
        result=new ArrayList();
        dfs(s.length()-1,new Stack(),s);
        Collections.reverse(result); //emmmm...加了这个就A了，出题人脑回路清奇，还限定了输出顺序。
        return result;
    }


    @SuppressWarnings("unchecked")
    private static void dfs(int pos, Stack st,String s){
        if(pos==-1){ //从后面往前遍历 找到即把结果拼接存到result里面
            Stack re= (Stack) st.clone();
            StringBuilder sb=new StringBuilder();
            while (!re.isEmpty()){
                if(re.size()>1){
                    sb.append(re.pop()).append(" ");
                }else{
                    sb.append(re.pop());
                }
            }
            result.add(sb.toString());
            return;
        }
        //这里表示
        //例如 catsand 
        //1.catsand
        //2.atsand
        //3.tsand 
        //4.sand 匹配 则压入栈->继续查找0～pos-1的字符串
        //5.and 
        ...
        //7.d
        for (int i = 0; i <= pos; i++) {
            if(dp[i][pos-i]==1){
                st.push(s.substring(i,pos+1));
                dfs(i-1,st,s);
                st.pop(); //回溯
            }
        }
    }

    private static int check(String s,Set dict){
        if(dict.contains(s)){
            return 1;
        }
        return 0;
    }

    public static void main(String[] args) {
        String s="catsanddog";
        String[] dict ={"cat", "cats", "and", "sand", "dog"};
        Set set=new HashSet(Arrays.asList(dict));
        wordBreak(s,set);
        System.out.println(result);
    }

4.word-break

Given a string s and a dictionary of words dict, determine if s can be segmented into a space-separated sequence of one or more dictionary words.
For example, given
s =”leetcode”,
dict =[“leet”, “code”].
Return true because”leetcode”can be segmented as”leet code”.

//解法一：
dp[i]代表在i之前的数字是已经匹配过且符合条件的。
 0 1 2 3 4 5 6 7 8
 l e e t c o d e
当i=4，j=0时候，我们s.substring(0,4)刚好在dirt中，并且dp[j]=true,
那么我们就将dp[i]放置为true,即dp[4]=true,表示在i=4之前的子串即leet是符合条件的，        
当我们i=8，j=4时，s.substring(4,8)即code在dirt中，且dp[j]=true，那么说明这串是符合条件的。
public class _19 {
    public boolean wordBreak(String s, Set dict) {
        int len=s.length();
        boolean[] dp=new boolean[len+1];
        dp[0]=true;
        for (int i = 1; i <= len; i++) {
            for (int j = 0; j < i; j++) {
                if(dict.contains(s.substring(j,i))&&dp[j]){
                   dp[i]=true;
                }
            }
        }
        return dp[len];
    }
}
解法二：和word-break-ii类似，dfs找出一种情况即返回true即可。
public class _18 {
    private static boolean[][] dp;
    private static int len;
    private boolean flag;
    public boolean wordBreak(String s, Set dict) {
        len=s.length();
        dp=new boolean[len+1][len+1];
        for (int i = 0; i < len; i++) {
            for (int j = 0; j < len-i; j++) {
                dp[i][j]=dict.contains(s.substring(i,i+j+1));
            }
        }
        dfs(s.length()-1);
        if(flag){
            flag=false;
            return true;
        }
        return false;
    }
    private void dfs(int pos){
        if(flag==true){
            return;
        }
        if(pos==-1){
            flag=true;
        }
        for (int i = 0; i <= pos; i++) {
            if(dp[i][pos-i]){
                dfs(i-1);
            }
        }
    }
    public static void main(String[] args) {
        String s ="a";
        String[] ss={"a"};
        Set dict=new HashSet(Arrays.asList(ss));
        System.out.println(new _18().wordBreak(s,dict));
    }
}

5.candy

There are N children standing in a line. Each child is assigned a rating value.
You are giving candies to these children subjected to the following requirements:
Each child must have at least one candy.
Children with a higher rating get more candies than their neighbors.
What is the minimum candies you must give?
思路:dp[i]代表当前位置所需要的糖果数目。我们正着跑一遍，反着跑一遍即可。

public class _20 {
    public int candy(int[] ratings) {
        int n=ratings.length;
        int[] dp=new int[n+1];
        Arrays.fill(dp,1);
        for (int i = 1; i < n; i++) {
            if (ratings[i] > ratings[i - 1]) {//当前值比前一位的大 当前值在前一位的基础上+1
                dp[i] = dp[i - 1] + 1;
            }
        }
        for (int j = n-2; j >= 0; --j) {
            if(ratings[j]>ratings[j+1]&&dp[j]<=dp[j+1]){ //当前值比他的后面以为要大，且dp的值要小的话，那么就dp[j]=dp[j+1]+1;
                dp[j]=dp[j+1]+1;
            }
        }
        int res=0;
        for (int i = 0; i < n; i++) {
            res+=dp[i];
        }
        return res;
    }
    public static void main(String[] args) {
        int[] a=new int[]{4,2,3,4,1};
        System.out.println(new _20().candy(a));
    }
}

6.leetCode palindrome-partitioning

Given a string s, partition s such that every substring of the partition is a palindrome.
Return all possible palindrome partitioning of s.
For example, given s =”aab”,
Return
[
[“aa”,”b”],
[“a”,”a”,”b”]
]
思路:dp[i][j]表示从第i位到第j位是不是回文串。
O(n^2)求出所有的回文串。
然后dfs从后往前找一遍存下所有的情况。
记得按字典序排序。

import java.util.ArrayList;
import java.util.Collections;
import java.util.Comparator;
import java.util.Stack;

public class _21 {
    static int[][] dp;
    static ArrayList> result;
    public ArrayList> partition(String s) {
        result=new ArrayList>();
        int len=s.length();
        dp=new int[len+1][len+1];
        for (int i = 0; i < len; i++) {
            dp[i][i]=1; 
        }
        for (int i = 0; i < len; i++) { //求出所有的回文
            for (int j = 0; j < i; j++) {
                if(s.charAt(i)==s.charAt(j)){
                    if(j+1==i){
                        dp[j][i]=1;
                    }else{
                        dp[j][i]=dp[j+1][i-1];
                    }
                }
            }
        }
        dfs(s.length()-1,new Stack(),s);
        Collections.sort( result, new Comparator>() {
            @Override
            public int compare(ArrayList strings, ArrayList t1) {
                for (int i = 0; i < strings.size(); i++) { //按字典序排序
                    int re=strings.get(i).compareTo(t1.get(i));
                    if(re>0){
                        return 1;
                    }else if(re==0){
                        continue;
                    }else {
                        return -1;
                    }
                }
                return -1;
            }
        } );
        return result;
    }
    @SuppressWarnings("unchecked")
    private void dfs(int pos, Stack stack,String s){
        if(pos==-1){
              ArrayList strings=new ArrayList();
              Stack st= (Stack) stack.clone();
              while (!st.isEmpty()){
                  strings.add(st.pop());
              }
              result.add(strings);
              return;
        }

        for (int i = 0; i <= pos; i++) {
            if(dp[i][pos]==1){
                stack.push(s.substring(i,pos+1));
                dfs(i-1,stack,s);
                stack.pop();
            }
        }

    }
    public static void main(String[] args) {
        String s="fff";
        new _21().partition(s);
        System.out.println(result);
    }
}

7.palindrome-partitioning-ii
Given a string s, partition s such that every substring of the partition is a palindrome.
Return the minimum cuts needed for a palindrome partitioning of s.
For example, given s =”aab”,
Return1since the palindrome partitioning[“aa”,”b”]could be produced using 1 cut.
题目要求把s分割成所有子串都是求回文串的最小割。
首先呢，我们先用f[i][j]保存从i到j的子串是否是回文串。
然后有dp[i]表示从i到len-1的最小割。
dp[len]设置为-1表示dp[len-1]是回文串的话，那他不需要割，因为它是最后一个节点。
状态转移方程就是dp[i]=min{dp[i],dp[j+1]+1}
j表示是i~len-1的一个中介点，即f[i][j]到f[j+1][len-1]之间割一刀(d[j+1]表示的是f[j+1][len-1]的最小割).

import java.util.Arrays;
public class _22 {

    static boolean[][] f;
    static int[] dp;
    static int max=0x7FFFFFF;

    public int minCut(String s) {
        int len=s.length();
        f=new boolean[len+1][len+1];
        for (int i = 0; i < len; i++) {
            f[i][i]=true;
        }
        for (int i = 0; i < len; i++) {
            for (int j = 0; j <= i-1; j++) {
                if(s.charAt(i)==s.charAt(j)){
                    if(j+1==i){
                        f[j][i]=true;
                    }else {
                        f[j][i]=f[j+1][i-1];
                    }
                }
            }
        }
        dp=new int[len+1];
        Arrays.fill(dp,0x3FFFFFF);
        dp[len]=-1;
        for (int i = len-1; i >= 0; --i) {
            for (int j = i; j < len; j++) {
                if(f[i][j]){
                    dp[i]=Math.min(dp[i],dp[j+1]+1);
                }
            }
        }
        return dp[0];

    }
     public static void main(String[] args) {
        String s="abbab";
        System.out.println(new _22().minCut(s));
    }

}

8.distinct-subsequences
Given a string S and a string T, count the number of distinct subsequences of T in S.
A subsequence of a string is a new string which is formed from the original string by deleting some (can be none) of the characters without disturbing the relative positions of the remaining characters. (ie,”ACE”is a subsequence of”ABCDE”while”AEC”is not).
Here is an example:
S =”rabbbit”, T =”rabbit”
Return3.
思路：
dp[i][j]表示S串第i位与T串第j位当前匹配上的数目。
若S串不使用第i个字符，那么dp[i][j]=dp[i-1][j]
若S[i]==T[j]，那么dp[i][j]=dp[i-1][j-1]+dp[i-1][j] //为什么要加上dp[i-1][j]呢，因为我们上面说过了，我们可以不使用第i个字符，也能够用T串匹配S串。这里要算上使用该字符和不使用该字符的情况。如样例：rabbbit rabbit 我们可以使用S串第三个字符匹配T串第3个字符，也可以不使用第三个(使用第4个，或者第5个)。
若S[i]!=T[j],那么dp[i][j]=dp[i-1][j]

public class _23 {
    public int numDistinct(String S, String T) {
        int n=S.length();
        int m=T.length();
        int dp[][]=new int[n+1][m+1];
        for (int i = 0; i < n; i++) {
            dp[i][0]=1;
        }
        for (int i = 1; i <= n; i++) {
            for (int j = 1; j <= m; j++) {
                if(S.charAt(i-1)==T.charAt(j-1)){
                    dp[i][j]=dp[i-1][j-1]+dp[i-1][j];
                }else{
                    dp[i][j]=dp[i-1][j];
                }
            }
        }
        return dp[n][m];
    }
    public static void main(String[] args) {
        System.out.println(new _23().numDistinct("rabbbit","rabit"));
    }
}

9.triangle
Given a triangle, find the minimum path sum from top to bottom. Each step you may move to adjacent numbers on the row below.
For example, given the following triangle
[
[2],
[3,4],
[6,5,7],
[4,1,8,3]
]
The minimum path sum from top to bottom is11(i.e., 2 + 3 + 5 + 1 = 11).
Note:
Bonus point if you are able to do this using only O(n) extra space, where n is the total number of rows in the triangle.
状态转移方程:dp[i][j]=dp[i][j]+min{dp[i-1,j-1],dp[i-1,j]}.
注意一下边界即可。

public class _24 {
    public int minimumTotal(ArrayList> triangle) {
        int n=triangle.size();
        int[][] f=new int[n+1][n+1];
        for (int i = 1; i <= n; i++) {
            ArrayList ar=triangle.get(i-1);
            for (int j = 1; j <= i; j++) {
                if(j==1){
                    f[i][j]=ar.get(j-1)+f[i-1][j];
                }else if(j==i){
                    f[i][j]=ar.get(j-1)+f[i-1][j-1];
                }else{
                    f[i][j]=ar.get(j-1)+Math.min(f[i-1][j],f[i-1][j-1]);
                }
            }
        }
        int res=0x3FFFFFF;
        for (int i = 1; i <= n; i++) {
            res=Math.min(res,f[n][i]);
        }
        return res;
    }
    public static void main(String[] args) {
        ArrayList > res=new ArrayList>();
        ArrayList R1=new ArrayList();
        R1.add(-10);
        res.add(R1);
        System.out.println(new _24().minimumTotal(res));
    }
}

10.interleaving-string
Given s1, s2, s3, find whether s3 is formed by the interleaving of s1 and s2.
For example,
Given:
s1 =”aabcc”,
s2 =”dbbca”,
When s3 =”aadbbcbcac”, return true.
When s3 =”aadbbbaccc”, return false.
dp[i][j]表示s1前i个字符与s2前j个字符是否与s3前i+j个字符匹配。
状态转移方程:
dp{i,j}=dp{i-1,j}&&S1[i-1]==S3[i+j-1] || dp{i,j-1}&&S2[j-1]==S3[i+j-1]
则表示我可以用s1的第i个字符与s3的第i+j个字符匹配或者用s2的第j个字符与s3的第j+1个字符匹配，
只要有一种情况成立即可。

public class _25 {
    public boolean isInterleave(String s1, String s2, String s3) {
        int n=s1.length();
        int m=s2.length();
        if(n+m!=s3.length()){
            return false;
        }
        char[] c1=s1.toCharArray();
        char[] c2=s2.toCharArray();
        char[] c3=s3.toCharArray();
        boolean[][] dp=new boolean[n+1][m+1];
        dp[0][0]=true; //默认还没开始匹配为true
        for (int i = 1; i <= n; i++) {
            dp[i][0]=(c1[i-1]==c3[i-1]);
        }
        for (int i = 1; i <= m; i++) {
            dp[0][i]=(c2[i-1]==c3[i-1]);  
        }
        for (int i = 1; i <= n; i++) {
            for (int j = 1; j <= m; j++) {
                dp[i][j]=dp[i-1][j]&&(c1[i-1]==c3[i+j-1])
                        ||dp[i][j-1]&&(c2[j-1]==c3[i+j-1]);
            }
        }
        return dp[n][m];
    }

    public static void main(String[] args) {
        System.out.println(new _25().isInterleave("aabcc","dbbca","aadbbbaccc"));
    }

}

11.decode-ways

A message containing letters fromA-Zis being encoded to numbers using the following mapping:
‘A’ -> 1
‘B’ -> 2
…
‘Z’ -> 26
Given an encoded message containing digits, determine the total number of ways to decode it.
For example,
Given encoded message”12”, it could be decoded as”AB”(1 2) or”L”(12).
The number of ways decoding”12”is 2.
首先先考虑不组合成2位数的情况。
123 第2位不为0 那么他就是 12自由组合的情况下 再加上3 所以有dp[i]=dp[i-1]
再考虑组合成2位数的情况。
123 第1位和第2位组合成一个2位数 那么就是 在1自由组合的情况下 再加上23 所以有dp[i]+=dp[i-2].
要注意一下0的情况。

public class _26 {
    public int numDecodings(String s) {
        if(s.length()==0||s.charAt(0)=='0'){ //开头为0则直接返回0.
            return 0;
        }
        int n=s.length();
        char[] chars=s.toCharArray();
        int[] dp=new int[n+1];
        dp[0]=1;  
        dp[1]=1;  
        for (int i=2;i<=n;++i){ //从2开始会好分析一点。
            if(chars[i-1]>'0'){ //若i-1位为0，那么我们不能取i-1前的所有情况 因为这样子会把0单独划开的情况加进去。例如10.   
                dp[i]=dp[i-1];
            }
            if(chars[i-2]=='1'||(chars[i-2]=='2'&&chars[i-1]<='6'&&chars[i-1]>='0')){//分析可以组成2位的情况 
               dp[i]+=dp[i-2]; //那就就直接加上dp[i-2]的意思是我们把(i-1,i-2)组合成一个 例如 123-> 1 23 
            }
        }
        return dp[n];
    }
    public static void main(String[] args) {
        System.out.println(new _26().numDecodings("101"));
    }
}

12.unique-paths

A robot is located at the top-left corner of a m x n grid (marked ‘Start’ in the diagram below).
The robot can only move either down or right at any point in time. The robot is trying to reach the bottom-right corner of the grid (marked ‘Finish’ in the diagram below).
How many posible unique paths are there?

状态转移方程:dp[i][j]=dp[i-1][j]+dp[i][j-1]

public class _27 {
    public int uniquePaths(int m, int n) {
        int[][] dp=new int[m+1][n+1];
        for (int i = 1; i <= m; i++) {
            dp[i][1]=1;
        }
        for (int i = 1; i <= n; i++) {
            dp[1][i]=1;
        }
        for (int i = 2; i <= m; i++) {
            for (int j = 2; j <= n; j++) {
                dp[i][j]=dp[i-1][j]+dp[i][j-1];
            }
        }
        return dp[m][n];
    }
    public static void main(String[] args) {
        System.out.println(new _27().uniquePaths(2,1));
    }
}

13.unique-paths-ii

Follow up for “Unique Paths”:
Now consider if some obstacles are added to the grids. How many unique paths would there be?
An obstacle and empty space is marked as1and0respectively in the grid.
For example,
There is one obstacle in the middle of a 3x3 grid as illustrated below.
[
[0,0,0],
[0,1,0],
[0,0,0]
]
The total number of unique paths is2.
Note: m and n will be at most 100.
思路:
若m[i-1][j]==1&&m[i][j-1]==1,dp[i][j]=0;
若m[i-1][j]==1&&m[i][j-1]!=1,dp[i][j]=dp[i][j-1]
若m[i-1][j]!=1&&m[i][j-1]==1,dp[i][j]=dp[i-1][j]
若m[i-1][j]==0&&m[i][j-1]==0,dp[i][j]=dp[i-1][j]+dp[i][j-1];

public class _28 {
    public int uniquePathsWithObstacles(int[][] obstacleGrid) {
        int n=obstacleGrid.length;
        int m=obstacleGrid[0].length;
        int[][] dp=new int[n][m];
        if(obstacleGrid[0][0]!=1){
            dp[0][0]=1;
        }
        for (int i = 1; i < n; i++) {
            if(obstacleGrid[i][0]==0&&dp[i-1][0]==1){ //考虑 0 1 0 0 0 的情况 后都是不可走的被阻塞了
                dp[i][0]=1;
            }
        }
        for (int i = 1; i < m; i++) {
            if(obstacleGrid[0][i]==0&&dp[0][i-1]==1){ //同上
                dp[0][i]=1;
            }
        }
        for (int i = 1; i < n; i++) {
            for (int j = 1; j < m; j++) {
                if(obstacleGrid[i][j]==1){
                    continue;
                }
                if(obstacleGrid[i-1][j]==1&&obstacleGrid[i-1][j]==1){
                    dp[i][j]=0;
                }
                 if(obstacleGrid[i-1][j]==1){
                    dp[i][j]=dp[i][j-1];
                }else if(obstacleGrid[i][j-1]==1){
                    dp[i][j]=dp[i-1][j];           
                }else {
                    dp[i][j]=dp[i-1][j]+dp[i][j-1];
                }
            }
        }
        return dp[n-1][m-1];

    }
    public static void main(String[] args) {
        int[][] a=new int[1][2];
        a[0][0]=1;
        System.out.println(new _28().uniquePathsWithObstacles(a));
    }
}

14.climbing-stairs

You are climbing a stair case. It takes n steps to reach to the top.
Each time you can either climb 1 or 2 steps. In how many distinct ways can you climb to the top?
这道题没什么好说的。转移方程: dp[i]=dp[i-1]+dp[i-2];

public class _29 {
    public int climbStairs(int n) {
        if(n<=2){
            return n;
        }
        int[] dp=new int[n+1];
        dp[1]=1;
        dp[2]=2;
        for (int i = 3; i <= n; i++) {
            dp[i]=dp[i-1]+dp[i-2];
        }
        return dp[n];
    }
}

15.minimum-path-sum

Given a m x n grid filled with non-negative numbers, find a path from top left to bottom right which minimizes the sum of all numbers along its path.
这也没什么好讲的。状态转移方程: dp{i,j}=grid{i,j}+min{dp{i-1,j},dp{i,j-1}}

Note: You can only move either down or right at any point in time.

public class _30 {
    public int minPathSum(int[][] grid) {
        int n = grid.length;
        int m = grid[0].length;
        int[][] dp = new int[n][m];
        dp[0][0] = grid[0][0];
        for (int i = 1; i < m; ++i) {
            dp[0][i] = grid[0][i] + dp[0][i-1];
        }
        for (int i = 1; i < n; i++) {
            dp[i][0] = grid[i][0] + dp[i-1][0];
        }
        for (int i = 1; i < n; i++) {
            for (int j = 1; j < m; j++) {
                dp[i][j] = grid[i][j] + Math.min( dp[i - 1][j], dp[i][j - 1] );
            }
        }
        return dp[n - 1][m - 1];
    }

    public static void main(String[] args) {
        int[][] grid={{1,3,1},{1,5,1},{4,2,1}};
        System.out.println(new _30().minPathSum(grid));
    }
}

16.edit-distance

Given two words word1 and word2, find the minimum number of steps required to convert word1 to word2. (each operation is counted as 1 step.)
You have the following 3 operations permitted on a word:
a) Insert a character
b) Delete a character
c) Replace a character
如果c1[i-1]==c2[i-1],dp[i][j]=dp[i-1][j-1] 若相等，不需要进行操作。
如果c1[i-1]!=c2[i-1],dp[i][j]=min(dp[i-1][j]+1,dp[i-1][j-1]+1,dp[i][j-1]+1));
dp[i-1][j]表示s1第i-1位添加一个字符(或者删除一个字符),使得该字符与s2第j位的字符相等，操作数+1.
dp[i-1][j-1] 表示修改s1第i位字符和s2第j位字符，操作数+1.
dp[i][j-1] 表示的是删除s2第i位的字符，操作数+1.(或者添加一个字符)

public class _31 {
    public int minDistance(String word1, String word2) {
        char[] c1=word1.toCharArray();
        char[] c2=word2.toCharArray();
        int n=c1.length;
        int m=c2.length;
        int[][] dp=new int[n+1][m+1];
        for (int i = 0; i <= m; i++) { //表示s1 0个字符串变到s2第i个字符串最多需要的操作。
            dp[0][i]=i;
        }
        for (int i = 0; i <= n; i++) { //表示s2 0个字符串变到s1第i个字符串最多需要的操作。
            dp[i][0]=i;
        }
        for (int i = 1; i <= n; i++) {
            for (int j = 1; j <= m; j++) {
                if(c1[i-1]==c2[j-1]){
                    dp[i][j]=dp[i-1][j-1];
                }else{
                    dp[i][j]=Math.min(dp[i-1][j]+1,Math.min(dp[i-1][j-1]+1,dp[i][j-1]+1));
                }
            }
        }
        return dp[n][m];
    }
    public static void main(String[] args) {
        String s1="abc";
        String s2="abccd";
        System.out.println(new _31().minDistance(s1,s2));
    }
}

17.subsets

Given a set of distinct integers, S, return all possible subsets.
Note:
Elements in a subset must be in non-descending order.
The solution set must not contain duplicate subsets.

For example,
If S =[1,2,3], a solution is:
[
[3],
[1],
[2],
[1,2,3],
[1,3],
[2,3],
[1,2],
[]
]
思路:dfs即可。
要求非递减序列，那么我们先排序一遍。
然后按subset子集从小到大搜索一遍即可。

public class _32 {
    ArrayList> list;
    public ArrayList> subsets(int[] S) {
        list=new ArrayList>();
        Arrays.sort(S);
        list.add(new ArrayList());
        for (int i = 1; i <= S.length; i++) {
            dfs(0,i,new ArrayList(),S);
        }
        return list;
    }
    @SuppressWarnings("unchecked") 
    private void dfs(int st,int ed,ArrayList l,int[] S){ //ed代表subset的元素数量。
        if(ed==-1){
            return;
        }
        if(ed==0){
            list.add((ArrayList)l.clone());
        }
        for (int i = st; i < S.length; i++) {
            l.add(S[i]);
            dfs(i+1,ed-1,l,S);
            l.remove(l.size()-1);
        }
    }

    public static void main(String[] args) {
        int[] s={1,2};
        System.out.println(new _32().subsets(s));
    }
}

18.subsets-ii

Given a collection of integers that might contain duplicates, S, return all possible subsets.
Note:
Elements in a subset must be in non-descending order.
The solution set must not contain duplicate subsets.
For example,
If S =[1,2,2], a solution is:
[
[2],
[1],
[1,2,2],
[2,2],
[1,2],
[]
]
思路，和18一样，加个查重判断即可。
或者:加个判断，如果当前值与前一个值的值相等，则跳过，见法二。

public class _33 {
    ArrayList > list;
    public ArrayList> subsetsWithDup(int[] num) {
        list=new ArrayList>();
        Arrays.sort(num);
        list.add(new ArrayList());
        for (int i = 1; i <= num.length; i++) {
            dfs(0,i,new ArrayList(),num);
        }
        Collections.sort(list,new Comparator>(){ //将结果排序
            @Override
            public int compare(ArrayList integers, ArrayList t1) {
                for (int i = 0; i < integers.size(); i++) {
                    if(i<=t1.size()-1){
                        int t=integers.get(i)-t1.get(i);
                        if(t!=0){
                            return t;
                        }
                    }else{
                        return 1;
                    }
                }
                return -1;
            }
        } );
        return list;
    }
    @SuppressWarnings("unchecked")
    private void dfs(int st,int count,ArrayList l,int[] num){
        if(count==-1){
            return;
        }
        if(count==0){
            if(list.contains(l)){
                return;
            }else{
                list.add( (ArrayList) l.clone() );
            }
        }
        for (int i = st; i < num.length; i++) {
            l.add(num[i]);
            dfs(i+1,count-1,l,num);
            l.remove(l.size()-1);
        }
    }

    public static void main(String[] args) {
        int[] num={1,2};
        System.out.println(new _33().subsetsWithDup(num));
    }
}
法二：
 ArrayList > list;
    public ArrayList> subsetsWithDup(int[] num) {
        list=new ArrayList>();
        Arrays.sort(num);
        dfs(new ArrayList(),num,0);
        return list;
    }
    @SuppressWarnings("unchecked")
    private void dfs(ArrayList l,int[] num,int st){
        list.add( (ArrayList) l.clone() );
        for (int i = st; i < num.length; i++) {
            if(i>st&&num[i]==num[i-1]){ //例如 2,3,3  2,3已经加入list，回溯，发现n3==n2,则不需要再加入了。
                continue;
            }
            l.add(num[i]);
            dfs(l,num,i+1);
            l.remove(l.size()-1);
        }
    }

19.gray code

The gray code is a binary numeral system where two successive values differ in only one bit.
Given a non-negative integer n representing the total number of bits in the code, print the sequence of gray code. A gray code sequence must begin with 0.
For example, given n = 2, return[0,1,3,2]. Its gray code sequence is:
00 - 0
01 - 1
11 - 3
10 - 2
Note:
For a given n, a gray code sequence is not uniquely defined.
For example,[0,2,3,1]is also a valid gray code sequence according to the above definition.
For now, the judge is able to judge based on one instance of gray code sequence. Sorry about that.
原理: 若二进制格雷码表示为: G[N-1]G[N-2]…G[2]G[1]G[0];
相应地, 则二进制码表示为: B[N-1]B[N-2]…B[2]B[1]B[0].
其中最高位保留: B[N-1] = G[N-1];
其他各位: B[i-1] = G[i-1] xor B[i]. (i = 1, 2, …, n-1)

public class _35 {
    public ArrayList grayCode(int n) {
        ArrayList vector=new ArrayList();
        for (int i = 0; i < Math.pow(2,n); i++) {
            vector.add((i>>1)^i);
        }
        return vector;
    }
}

20.sort-list

Sort a linked list in O(n log n) time using constant space complexity.
链表 O(nlogn)可以使用归并排序
利用分治策略。
具体可以去看归并排序相关的blog.

public class _36 {
    public ListNode sortList(ListNode head) {
        if(head==null||head.next==null){
            return head;
        }
        ListNode mid=getMid(head); //找中点
        ListNode midNext=mid.next; 
        mid.next=null;
        return merge(sortList(head),sortList(midNext));
    }
    //获得中点 利用快慢指针
    public ListNode getMid(ListNode head){
        ListNode slow=head;
        ListNode quick=head;
        while (quick.next!=null&&quick.next.next!=null){
            slow=slow.next;
            quick=quick.next.next;
        }
        return slow;
    }
    //合并
    public ListNode merge(ListNode l,ListNode r){ 
        ListNode head=new ListNode(-1),
                cur=head,cur1=l,cur2=r;
        while (cur1!=null&&cur2!=null){
            if(cur1.valelse {
                cur.next=cur2;
                cur2=cur2.next;
            }
            cur=cur.next;
        }
        cur.next=cur1==null?cur2:cur1;
        return head.next;
    }
    public static void main(String[] args) {
        //int[] a=new int[]{8,4,5,7,1,3,6,2};
        int[] a=new int[]{3,2,4};
        ListNode listNode=InsertUtil.build(a);
        listNode=new _36().sortList(listNode);
        while (listNode!=null){
            System.out.println(listNode.val);
            listNode=listNode.next;
        }
    }
}

21.insertion-sort-list

Sort a linked list using insertion sort.

public class _37 {
    public ListNode insertionSortList(ListNode head) {
        if(head==null||head.next==null){
            return head;
        }
        ListNode res=new ListNode(-1); //新建一个数组保存排序后的值
        ListNode pre; //遍历排序后数组
        ListNode cur=head; //遍历未排序的数组
        while (cur!=null){
            ListNode next=cur.next; //保存当前数组的下一个数组
            pre=res;
            while (pre.next!=null&&pre.next.val//找到第一个比cur大的
                pre=pre.next;
            }
            cur.next=pre.next; //把cur的val值插入
            pre.next=cur;
            cur=next;
        }
        return res.next;
    }
    public static void main(String[] args) {
        int[] a=new int[]{8,4,5,7,1,3,6,2};
        //int[] a=new int[]{3,2,4};
        ListNode listNode=InsertUtil.build(a);
        listNode=new _37().insertionSortList(listNode);
        while (listNode!=null){
            System.out.println(listNode.val);
            listNode=listNode.next;
        }
    }
}

22.binary-tree-postorder-traversal

Given a binary tree, return the postorder traversal of its nodes’ values.
For example:
Given binary tree{1,#,2,3},
1
\
2
/
3
return[3,2,1].
Note: Recursive solution is trivial, could you do it iteratively?
深搜一遍即可，左->右->根

public class _38 {
    ArrayList res;
    public ArrayList postorderTraversal(TreeNode root) {
        if(root==null){
            return new ArrayList();
        }
        res=new ArrayList();
        dfs(root);
        return res;
    }
    public void dfs(TreeNode root){
        if(root.left!=null){
            dfs(root.left);
        }
        if(root.right!=null){
            dfs(root.right);
        }
        res.add(root.val);
    }
}

24. binary-tree-preorder-traversal

Given a binary tree, return the preorder traversal of its nodes’ values.
For example:
Given binary tree{1,#,2,3},
1
\
2
/
3
return[1,2,3].
Note: Recursive solution is trivial, could you do it iteratively?
深搜一遍即可，根->左->右

public class _39 {
    static class TreeNode {
        int val;
        TreeNode left;
        TreeNode right;
        TreeNode(int x) { val = x; }
    }
    ArrayList res;
    public ArrayList preorderTraversal(TreeNode root) {
        if(root==null){
            return new ArrayList();
        }
        res=new ArrayList();
        dfs(root);
        return res;
    }
    public void dfs(TreeNode root){
        res.add(root.val);
        if(root.left!=null){
            dfs(root.left);
        }
        if(root.right!=null){
            dfs(root.right);
        }
    }
    public static void main(String[] args) {
        TreeNode treeNode=new TreeNode(1);
        treeNode.right=new TreeNode(2);
        treeNode.right.left=new TreeNode(3);
        System.out.println(new _39().preorderTraversal(treeNode));
    } 
}

23.reorder-list

Given a singly linked list L: L 0→L 1→…→L n-1→L n,
reorder it to: L 0→L n →L 1→L n-1→L 2→L n-2→…
You must do this in-place without altering the nodes’ values.
For example,
Given{1,2,3,4}, reorder it to{1,4,2,3}.
使用快慢指针找中点，再翻转后一端。
遍历一遍即可。

public class _40 {

    public void reorderList(ListNode head) {
        if(head==null||head.next==null||head.next.next==null){ //直接有答案
            return;
        }
        ListNode slow=head;
        ListNode quick=head;
        while (quick.next!=null&&quick.next.next!=null){ //快慢指针找中点
            slow=slow.next;
            quick=quick.next.next;
        }
        ListNode midNext=slow.next;
        slow.next=null;
        ListNode pre=null;
        ListNode cur=midNext;
        while (cur!=null){  //翻转
            ListNode next=cur.next;
            cur.next=pre;
            pre=cur;
            cur=next;
        }
        ListNode newHead=new ListNode(-1); //新建存结果
        ListNode res=newHead;
        cur=head;
        int count=0;
        while (cur!=null||pre!=null){ //遍历一遍
            if(count%2==0){
                res.next=cur;
                cur=cur.next;
            }else{
                res.next=pre;
                pre=pre.next;
            }
            ++count;
            res=res.next;
        }
        head=newHead.next;  //赋值给head
    }
}

24.linked-list-cycle

Given a linked list, determine if it has a cycle in it.
Follow up:
Can you solve it without using extra space?
利用快慢指针，相遇即有环。

public class _41 {
    public boolean hasCycle(ListNode head) {
        if(head==null||head.next==null){
            return false;
        }
        ListNode slow=head;
        ListNode quick=head;
        while (quick.next!=null&&quick.next.next!=null){
            slow=slow.next;
            quick=quick.next.next;
            if(slow==quick){
                return true;
            }
        }
        return false;
    }
}

25.linked-list-cycle-ii

Given a linked list, return the node where the cycle begins. If there is no cycle, returnnull.
Follow up:
Can you solve it without using extra space?
首先呢，快慢指针判断有没有环，无环直接返回null.
那么怎么判断环的起点呢。
看图:

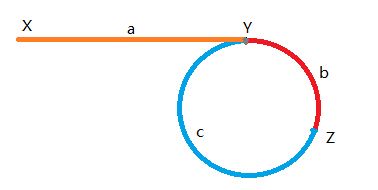
搬一下讨论区的图。
X为list的起点，Y为环入口的起点，Z为快慢指针的相遇的地点。
快慢指针相遇的t为：
(a+b)/v=(a+b+n*(b+c))/2v
自己可以画一下图，快慢指针相遇肯定是在慢指针走第一圈的范围内，不会在慢指针走第二圈的时候才相遇。
怎么证明呢，假设慢指针s刚到Y点，快指针f到达任意一点，那么s，y之间的距离就是m，s每次走一步，s，f之间的距离加减1，且x<=b+c,所以他们一定能够在s走完一圈的范围内相遇。
所以才有(a+b)/v=(a+b+n*(b+c))/2v
化为 a=(n-1)*b+nc -> a=(n-1)(b+c)+c
所以说，当一个指针x在X位置开始，另一个指针y在Z位置开始，
当x走完a，y恰好走完n-1圈并且走完C到Y点与x指针相遇。

public ListNode detectCycle(ListNode head) {
        if(head==null){
            return null;
        }
        ListNode slow=head;
        ListNode quick=head;
        while (quick.next!=null&&quick.next.next!=null){
            slow=slow.next;
            quick=quick.next.next;
            if(slow==quick){
                break;
            }
        }
        if(quick.next==null||quick.next.next==null){
            return null;
        }
        slow=head;
        while (slow!=quick){
            slow=slow.next;
            quick=quick.next;
        }
        return slow;
    }

26.single-number

Given an array of integers, every element appears twice except for one. Find that single one.
Note:
Your algorithm should have a linear runtime complexity. Could you implement it without using extra memory?
最佳解法:位运算，两个数异或为0

一
public class _44 {
    public static int singleNumber(int[] A) {
        Map map=new HashMap();
        for (int i = 0; i < A.length; i++) {
            if(map.containsKey(A[i])){
                map.put(A[i],2);
            }else {
                map.put(A[i],1);
            }
        }
        for (Map.Entry entry:map.entrySet()){
            if(entry.getValue()==1){
                return entry.getKey();
            }
        }
        return -1;
    }
    public static void main(String[] args) {
        int[] A={2,2,1,1,3};
        System.out.println(singleNumber(A));
    }
}
二
public class _45 {
    public int singleNumber(int[] A) {
        int res=A[0];
        for (int i = 1; i < A.length; i++) {
            res^=A[i];
        }
        return res;
    }
}

27.single-number-ii

Given an array of integers, every element appears three times except for one. Find that single one.
Note:
Your algorithm should have a linear runtime complexity. Could you implement it without using extra memory?
O(n)的做法是位运算。
one就是为了保存出现过一次的bit，two为了存出现过两次的bit，three就是为了保存出现过三次的bit。
首先呢，看two|=one&A[i]，&运算就是为了看哪个位置上的bit出现了两次，|运算就是为了保存那些出现过两次的bit上的1.
one^=A[i].异或运算，就是了出掉那些出现过两次的bit上的1.
three=one&two，保存那些出现过三次的bit的1.
one&=~three; 该bit上的1出现三次了，那么我能就把1和2上该位置的bit变成0.
ep: 5 3 5 5
首先5->101 two: 0 0 0 因为没有一位是出现过两次的，ones: 1 0 1 第1个bit上出现一次，第三个bit上出现1次。three依然是0.
3->011 two:0 0 1 因为第一位置上的bit出现了两次了。 ones：1 1 0 第一位bit出现两次，变成0.three已经是0.
5->101 two: 0 0 1 因为第1位置的1和第三位置的1在这里只是出现1而已。 ones: 1 1 1 三个位置的1都出现过一次。
three-> 0 0 1 因为第一位置的1在two出现两次，在one出现1次。然后我们把出现3次的bit在one two上去掉。
one-> 0 0 0 two-> 1 1 0.以此类推。

class _46{
    public static int singleNumber(int[] A) {
        int one=0;
        int two=0;
        int three;
        for (int i = 0; i < A.length; i++) {
            two|=one&A[i];
            one^=A[i];
            three=one&two;
            one&=~three;
            two&=~three;
        }
        return one;
    }
}